Chaos
Chaos, in many traditional cosmogonies, is the earliest state of the universe. Perhaps surprisingly, this is also the view of modern cosmologists. They see the universe starting in a state of "thermodynamical equilibrium" or maximum entropy about 13.7 billion years ago.
Chaos is often defined as the complete absence of order, and consequently of information. For the Greeks, the opposite of chaos was cosmos, an ordered and beautiful universe.
The Stoic
Chrysippus (200 B.C.E.) said that a single
uncaused cause could destroy the universe (cosmos), which would fall into chaos.
Everything that happens is followed by something else which depends on it by causal necessity. Likewise, everything that happens is preceded by something with which it is causally connected. For nothing exists or has come into being in the cosmos without a cause. The universe will be disrupted and disintegrate into pieces and cease to be a unity functioning as a single system, if any uncaused movement is introduced into it.
Chaos and the Kinetic Theory of Gases
The name "gas" was coined by a Dutch chemist as a variation on the word "chaos"
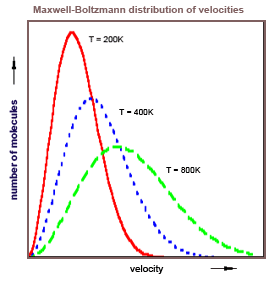
The closest thing to perfect chaos in a physical theory is a gas in thermodynamical equilibrium, a state of maximum disorder or maximum entropy. In such a state, the average number of gas particles per unit volume is the same everywhere in the gas. The distribution of velocities in any small volume large enough to contain a very large number of particles is the
Maxwell-
Boltzmann distribution.
In thermodynamic equilibriun, the average value of any gas property over time is the same as the average value over a large number of identical systems at the same time. This is called the
ergodic theorem.
Note that the kinetic theory of gases is a classical dynamical theory. It is thus a
deterministic theory. Gas particles are assumed to follow the laws of Newtonian mechanics. Boltzmann's first attempt to derive his H-Theorem (a proof of the second law of thermodynamics, that entropy should always increase), was criticized by his mentor,
Joseph Loschmidt, because since classical mechanical particle paths are time reversible, Boltzmann's proof of entropy increase would mean that if particles could be prepared in a starting with exactly opposite velocities, the entropy should decrease from such a starting state. This was called Loschmidt's
reversibility paradox.
Deterministic Chaos
In modern times a mathematical theory of deterministic chaos was developed, largely by computer scientists. They found that small rounding errors in their computer data (which has a limited number of significant figures) leads to large non-linear instabilities that expand exponentially in time and make long-term prediction impossible. This is the famous "butterfly wings in Beijing" effect discovered in weather predictions by the founder of chaos theory, the meteorologist
Edward Lorenz.
It is important to stress that there is nothing random or
undetermined (it involves no
quantum indeterminacy) about this mathematical chaos theory. Although it exhibits behaviors that resemble some phenomena in the real world, they are metaphors for behaviors, not physical explanations.
In addition, chaos should not be confused with
unpredictability, just as
determinism should not be confused with
predictability. The fundamental importance of chaos theory is its application to systems that are extremely sensitive to initial conditions. Chaotic systems are deterministic, but not predictable. Their unpredictability does not mean that they are random or indeterministic, as many philosophers and a few scientists who dislike quantum mechanics have mistakenly believed (e.g.,
Ilya Prigogine.
Some philosophers appear to believe that chaos theory can provide all the randomness need to prevent free will from being deterministic (e.g.,
Daniel Dennett). Some think that non-linear chaotic behavior disproves the determinism of
Laplace's super-intelligent demon. Laplace probably knew that the information required by the demon was unobtainable.
Isaac Newton certainly knew that his observations could not confirm his theory to arbitrary accuracy needed to prove perfect determinism.
Ludwig Boltzmann, his admirer and contemporary
Franz Exner, and Exner's student
Erwin Schrödinger often pointed out that deterministic theories
go beyond the available evidence. Popularization of physical theories has often confused not just the public, but even philosophers of science.
On the three hundredth anniversary of Newton’s
Principia, Sir James Lighthill gave a lecture to the Royal Society, lamenting the confusion between Newton's classical mechanical determinism and the apparent claim of perfect predictability:
”We are all deeply conscious today that the enthusiasm of our forebears for the marvellous achievements of Newtonian mechanics led them to make generalizations in this area of predictability which, indeed, we may have generally tended to believe before 1960, but which we now recognize were false. We collectively wish to apologize for having misled the general educated public by spreading ideas about determinism of systems satisfying Newton’s laws of motion that, after 1960,
were to be proved incorrect...”
(J. Lighthill, Proc. Roy. Soc. (London) A 407, 35 (1986))
Sensitivity to initial conditions was in fact known long before modern chaos theory and
complexity theory. James Clerk Maxwell noted in the 1860's that even if two molecules were adjacent to one another in a hydrodynamic flow, they might find themselves in random places in the container after relatively short mixing times. He wrote:
When the state of things is such that an infinitely small variation of the present state will alter only by an infinitely small quantity the state at some future time, the condition of the system, whether at rest or in motion, is said to be stable; but when an infinitely small variation in the present state may bring about a finite difference in the state of the system in a finite time, the condition of the system is said to be unstable.
The real world is only approximately classical mechanical (obeying Newton's dynamical laws at all scales). At the small scales of atomic and molecular physics, the world is quantum mechanical. There is nothing corresponding to deterministic chaos in quantum physics. Deterministic chaos requires continuous motion to produce mathematical singularities and exponential non-linearity. Despite unpredictable and spontaneous "quantum jumps," the discrete states of the quantum world are more regular and stable than their classical analogues. Indeed, the long-term stability of quantum structures in their "ground states" is astonishing, as is the complete indistinguishability of elementary particles, which gives rise to extremely non-intuitive statistics. Finally, the long-term stability of quantum cooperative phenomena is evident in the ability of biological macromolecules to maintain (by error detection and correction) their
information content.
The desire to describe randomness and chance in the world with deterministic chaos resembles the view of
Adolphe Quételet and
Henry Thomas Buckle that statistical regularities in various physical and social phenomena are evidence of an underlying determinism. Is the motivation similar to that which seeks an intelligent designer behind biological evolution? It seems that the "antipathy to chance" observed by
William James at the end of the nineteenth century is alive and well in the twenty-first.
For Teachers
To hide this material, click on the Normal link.
For Scholars
To hide this material, click on the Teacher or Normal link.
The Rise of Statistical Thinking, 1820-1900, by Theodore Porter, (Princeton, 1986) p.219-247, tells how Charles Sanders Peirce embraces chance as "Tychism." Porter also provides a summary of the influences of Renouvier, Fouillee, and Joseph Delbouef on Peirce.
The Taming of Chance, by Ian Hacking, (Cambridge, 1990) p.11, tells how Peirce attacked the doctrine of necessity. Hacking's thesis is that there was an "erosion of determinism" in the nineteenth century culminating in Peirce.
"To begin with, what is chance? The ancients
distinguished between the phenomena which seemed
to obey harmonious laws, established once for all,
and those that they attributed to chance, which were
those that could not be predicted because they were
not subject to any law. In each domain the precise
laws did not decide everything, they only marked
the limits within which chance was allowed to move.
In this conception, the word chance had a precise,
objective meaning; what was chance for one was
also chance for the other and even for the gods.
But this conception is not ours. We have become
complete determinists, and even those who wish to
reserve the right of human free will at least allow
determinism to reign undisputed in the inorganic
world. Every phenomenon, however trifling it be,
has a cause, and a mind infinitely powerful and
infinitely well-informed concerning the laws of nature
could have foreseen it from the beginning of the ages.
If a being with such a mind existed, we could play
no game of chance with him; we should always lose.
For him, in fact, the word chance would have no
meaning, or rather there would be no such thing as
chance."
(Science and Method, Henri Poincare, p.64)
"Just as no physicist will in the last resort acknowledge the play of chance in human nature, so no physiologist will admit the play of chance in the absolute sense."
Where Is Science Going, p.147.
"the assumption of chance in inorganic nature is incompatible with the working principle of natural science." Max Planck,
Where Is Science Going, p.154.
The De Moivre quote is cited in Hacking, Taming of Chance, p.13.
Normal |
Teacher |
Scholar