Paul Ehrenfest was a student in
Ludwig Boltzmann's classes on kinetic theory of gases at the University of Vienna. When Boltzmann committed suicide in 1906, Ehrenfest was chosen by the editors of the
Enzyklopädie der mathematischen Wissenschaften to prepare an article on the statistical mechanics of gases that Boltzmann had promised to write for them.
It took Ehrenfest, working with his wife Tatiana, five years to prepare the article, which later appeared as their book,
The Conceptual Foundations of the Statistical Approach in Mechanics.
The Ehrenfests reviewed Boltzmann's attempts to prove his H-Theorem, with emphasis on his
Stosszahlansatz (Collision Number Assumption) and the idea of "Molecular Chaos." Where other authors had sometimes identified these two assumptions, the Ehrenfests saw these as different assumptions.
The Ehrenfests greatly simplified the demonstration that particles would approach an equilibrium distribution. Where Boltzmann derived his result in the full generality of three dimensions with several pages of equations, the Ehrenfests produced a simple two-dimensional example.
They imagined an infinite plane with two kinds of “molecules.” P-molecules are infinitesimal points moving with constant speeds in four possible directions, right, up, left, and down, with corresponding distributions
f1, f2, f3, f4. The equilibrium distribution corresponding to Maxwell-Boltzmann equilibrium would be
f1 = f2 = f3 = f4 = N/4,
where N is the total number of P-molecules. The Q-molecules are fixed immovable squares on a diagonal as shown in the figure.
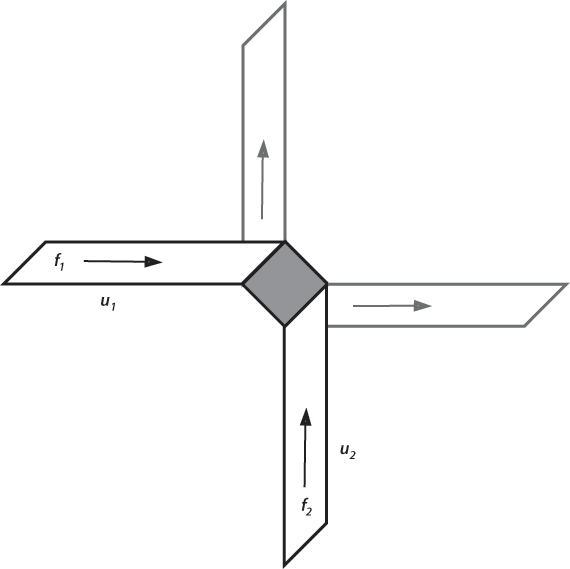
Ehrenfest’s 2-dimensional collisions.
Collisions of P-molecules with Q-molecules deflect the particles at right angles into one of the other distributions. The
Stosszahlansatz is equivalent to assuming that the number of P-molecules approaching the Q-molecule in the left-hand strip in the figure is proportional to the area of the strip, independent of the location in the plane.
If the distributions are not equal in the four directions, for example if
f2 >
f1, we can see that more
f2 upward-moving P-molecules would be deflected into the
f1 distribution than vice versa, thus tending toward equilibrium and demonstrating Boltzmann’s H-Theorem.
Ehrenfest showed Boltzmann’s physical intuitions to be correct. Numerical calculations confirm that gases at standard temperature and pressure reach equilibrium in the order of 10
-9 seconds, so what are we to make of the Loschmidt
microscopic reversibility criticism? That gases are not observed departing from thermal equilibrium and decreasing the entropy significantly and continuously is not to be found in the Boltzmann and Ehrenfest
Stosszahlansatz analyses, nor does it lie in the practical impossibility of reversing the velocities of all the particles.
Rather it is in the existence of quantum processes in colliding particles that exchange energy with the radiation field, randomly altering the angular momentum of the quasi-molecules and thus erasing the information memory of the exact paths that would be needed over millions of collisions to provide the microscopic reversibility needed to restore an initial state of low entropy.