Abraham de Moivre's classic book
The Doctrine of Chances (in three editions between 1718 and 1756) was basically a handbook for gamblers. It enabled them to know how to bet in various games of chance.
It begins...
The Probability of an Event is greater or less, according to the number of Chances by which it may happen, compared with the whole number of Chances by which it may happen or fail.
This brief statement contains the assumption that all states are equally probable, assuming that we have no
information that indicates otherwise.
While this describes our information
epistemically, making it a matter of human knowledge, we can say
ontologically that the world contains no information that would make any state more probable than the others. Such information simply does not exist. This is sometimes called the
principle of insufficient reason or the
principle of indifference.
If that information did exist, it could and would be revealed in large numbers of experimental trials, which provide the
statistics on the different "states."
Probabilities are a priori theories.
Statistics are a posteriori, the results of experiments.
In the philosophical controversies between
a priori or epistemic interpretations of
probability and
a posteriori or ontological interpretations, the latter are often said to be "frequency" interpretations of probability. We prefer to use the term statistics for these frequencies.
de Moivre's work underlies
James Clerk Maxwell's velocity distributions for the molecules in a gas, and
Ludwig Boltzmann's explanation for the increase of entropy in statistical mechanics (the second law of thermodynamics).
All other things being equal, any physical system evolves toward the macrostate with the greatest number of microstates consistent with the information contained in the macrostate. This
information is intrinsic to the system. It may be observable, but it in no way depends on being observed or "known" to any observer.
Probability Distributions
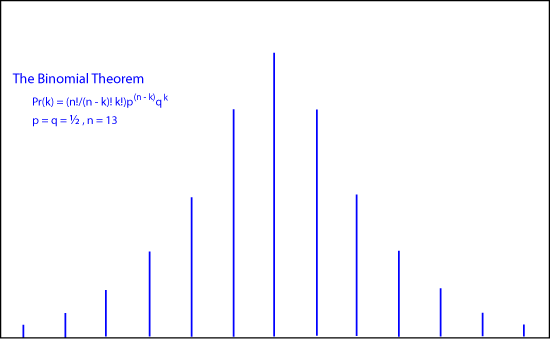
In his book, de Moivre worked out the mathematics for the binomial expansion of (
p -
q)
n by analyzing the tosses of a coin. If
p is the probability of a "heads" and
q = 1 -
p the probability of "tails," then the probability of
k heads is
Pr(k) = (n!/(n - k)! k!)p(n - k)qk
de Moivre also was the first to approximate the factorial for large
n as
n! ≈ (constant) √n nn e-n
James Stirling determined the constant in de Moivre's approximation ( = √(2π), which is now commonly called
Stirling's formula.
Using this approximation, which is valid for large numbers, de Moivre went on to approximate the
discrete binomial expansion with a
continuous curve.
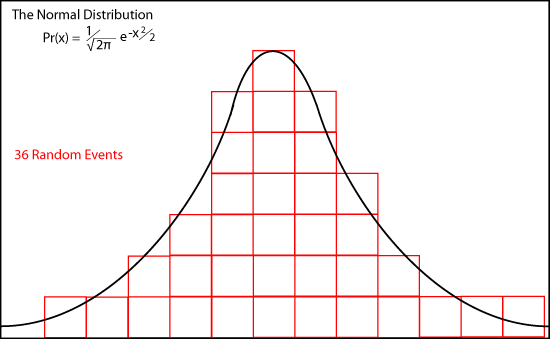
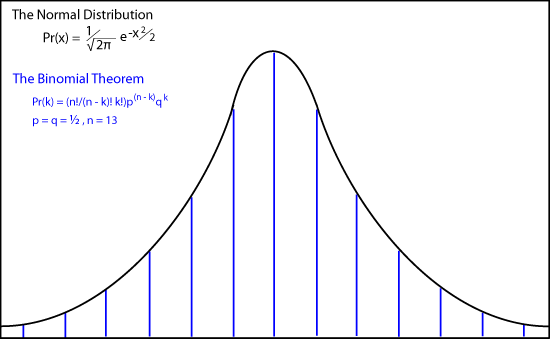
The animation shows how de Moivre's binomial coefficients approach the continuous "normal distribution or bell-shaped curve as
n approaches infinity.
Pr(x) = (1/√(2π)) e-x2/2
 Pierre-Simon Laplace
Pierre-Simon Laplace also derived this result, which is sometimes called the
de Moivre-Laplace Theorem. Laplace very likely knew of de Moivre's work, but gave him no credit, perhaps because of de Moivre's association with gambling, perhaps because de Moivre was a Huguenot protestant who had emigrated to England, or perhaps because Laplace's great works summarized much of the previous century's mathematics and science without giving credit to his predecessors.
Nearly 100 years later,
Legendre and
Gauss independently developed this curve as the distribution of measurement errors. It came to be poorly named the "law" of errors, misleading many philosophers to argue that random events were therefore lawful and each event must be determined somehow by this underlying lawfulness.
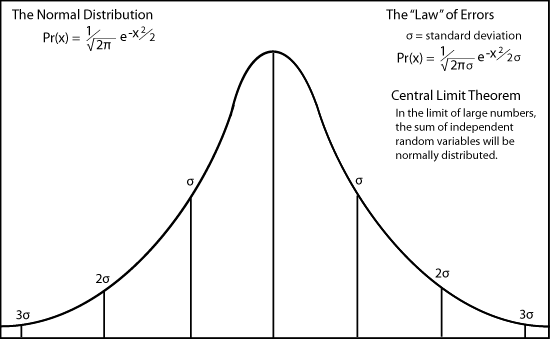
In order to derive de Moivre's curve as the distributions for errors, Legendre and Gauss made three assumptions - that errors are distributed symmetrically around a maximum value, that the value goes to zero for large positive and negative values of
x, and that the mean value of errors is the average value, namely zero.
In Laplace's hands, this tendency for the curve to peak around a maximum at the mean value in the limit of large numbers came to be called the
central limit theorem.
Today the principle of indifference (equiprobability assumption), the law of large numbers, and the central limit theorem are three of the fundamental postulates of
probability.
Carl Friedrich Gauss showed that the normal probability distribution explains the "method of least squares," which had been used by many scientists to establish the most probable value of an experimental measurement. Gauss showed that the most probable value is the average value (the mean) when errors in observations are distributed randomly.
Returning to de Moivre's original work, which was the chance occurrence of random events, it is very important to note that individual events are really random, despite their asymptotic approach to the normal distribution in the limit of large numbers of events. The material world itself is discrete and random, despite the idealization of the analytical continuous probability curve discovered first by de Moivre.