|
Philosophers
Mortimer Adler Rogers Albritton Alexander of Aphrodisias Samuel Alexander William Alston Anaximander G.E.M.Anscombe Anselm Louise Antony Thomas Aquinas Aristotle David Armstrong Harald Atmanspacher Robert Audi Augustine J.L.Austin A.J.Ayer Alexander Bain Mark Balaguer Jeffrey Barrett William Barrett William Belsham Henri Bergson George Berkeley Isaiah Berlin Richard J. Bernstein Bernard Berofsky Robert Bishop Max Black Susanne Bobzien Emil du Bois-Reymond Hilary Bok Laurence BonJour George Boole Émile Boutroux Daniel Boyd F.H.Bradley C.D.Broad Michael Burke Jeremy Butterfield Lawrence Cahoone C.A.Campbell Joseph Keim Campbell Rudolf Carnap Carneades Nancy Cartwright Gregg Caruso Ernst Cassirer David Chalmers Roderick Chisholm Chrysippus Cicero Tom Clark Randolph Clarke Samuel Clarke Anthony Collins Antonella Corradini Diodorus Cronus Jonathan Dancy Donald Davidson Mario De Caro Democritus Daniel Dennett Jacques Derrida René Descartes Richard Double Fred Dretske John Earman Laura Waddell Ekstrom Epictetus Epicurus Austin Farrer Herbert Feigl Arthur Fine John Martin Fischer Frederic Fitch Owen Flanagan Luciano Floridi Philippa Foot Alfred Fouilleé Harry Frankfurt Richard L. Franklin Bas van Fraassen Michael Frede Gottlob Frege Peter Geach Edmund Gettier Carl Ginet Alvin Goldman Gorgias Nicholas St. John Green H.Paul Grice Ian Hacking Ishtiyaque Haji Stuart Hampshire W.F.R.Hardie Sam Harris William Hasker R.M.Hare Georg W.F. Hegel Martin Heidegger Heraclitus R.E.Hobart Thomas Hobbes David Hodgson Shadsworth Hodgson Baron d'Holbach Ted Honderich Pamela Huby David Hume Ferenc Huoranszki Frank Jackson William James Lord Kames Robert Kane Immanuel Kant Tomis Kapitan Walter Kaufmann Jaegwon Kim William King Hilary Kornblith Christine Korsgaard Saul Kripke Thomas Kuhn Andrea Lavazza James Ladyman Christoph Lehner Keith Lehrer Gottfried Leibniz Jules Lequyer Leucippus Michael Levin Joseph Levine George Henry Lewes C.I.Lewis David Lewis Peter Lipton C. Lloyd Morgan John Locke Michael Lockwood Arthur O. Lovejoy E. Jonathan Lowe John R. Lucas Lucretius Alasdair MacIntyre Ruth Barcan Marcus Tim Maudlin James Martineau Nicholas Maxwell Storrs McCall Hugh McCann Colin McGinn Michael McKenna Brian McLaughlin John McTaggart Paul E. Meehl Uwe Meixner Alfred Mele Trenton Merricks John Stuart Mill Dickinson Miller G.E.Moore Ernest Nagel Thomas Nagel Otto Neurath Friedrich Nietzsche John Norton P.H.Nowell-Smith Robert Nozick William of Ockham Timothy O'Connor Parmenides David F. Pears Charles Sanders Peirce Derk Pereboom Steven Pinker U.T.Place Plato Karl Popper Porphyry Huw Price H.A.Prichard Protagoras Hilary Putnam Willard van Orman Quine Frank Ramsey Ayn Rand Michael Rea Thomas Reid Charles Renouvier Nicholas Rescher C.W.Rietdijk Richard Rorty Josiah Royce Bertrand Russell Paul Russell Gilbert Ryle Jean-Paul Sartre Kenneth Sayre T.M.Scanlon Moritz Schlick John Duns Scotus Arthur Schopenhauer John Searle Wilfrid Sellars David Shiang Alan Sidelle Ted Sider Henry Sidgwick Walter Sinnott-Armstrong Peter Slezak J.J.C.Smart Saul Smilansky Michael Smith Baruch Spinoza L. Susan Stebbing Isabelle Stengers George F. Stout Galen Strawson Peter Strawson Eleonore Stump Francisco Suárez Richard Taylor Kevin Timpe Mark Twain Peter Unger Peter van Inwagen Manuel Vargas John Venn Kadri Vihvelin Voltaire G.H. von Wright David Foster Wallace R. Jay Wallace W.G.Ward Ted Warfield Roy Weatherford C.F. von Weizsäcker William Whewell Alfred North Whitehead David Widerker David Wiggins Bernard Williams Timothy Williamson Ludwig Wittgenstein Susan Wolf Scientists David Albert Michael Arbib Walter Baade Bernard Baars Jeffrey Bada Leslie Ballentine Marcello Barbieri Gregory Bateson Horace Barlow John S. Bell Mara Beller Charles Bennett Ludwig von Bertalanffy Susan Blackmore Margaret Boden David Bohm Niels Bohr Ludwig Boltzmann Emile Borel Max Born Satyendra Nath Bose Walther Bothe Jean Bricmont Hans Briegel Leon Brillouin Stephen Brush Henry Thomas Buckle S. H. Burbury Melvin Calvin Donald Campbell Sadi Carnot Anthony Cashmore Eric Chaisson Gregory Chaitin Jean-Pierre Changeux Rudolf Clausius Arthur Holly Compton John Conway Simon Conway-Morris Jerry Coyne John Cramer Francis Crick E. P. Culverwell Antonio Damasio Olivier Darrigol Charles Darwin Richard Dawkins Terrence Deacon Lüder Deecke Richard Dedekind Louis de Broglie Stanislas Dehaene Max Delbrück Abraham de Moivre Bernard d'Espagnat Paul Dirac Hans Driesch John Dupré John Eccles Arthur Stanley Eddington Gerald Edelman Paul Ehrenfest Manfred Eigen Albert Einstein George F. R. Ellis Hugh Everett, III Franz Exner Richard Feynman R. A. Fisher David Foster Joseph Fourier Philipp Frank Steven Frautschi Edward Fredkin Augustin-Jean Fresnel Benjamin Gal-Or Howard Gardner Lila Gatlin Michael Gazzaniga Nicholas Georgescu-Roegen GianCarlo Ghirardi J. Willard Gibbs James J. Gibson Nicolas Gisin Paul Glimcher Thomas Gold A. O. Gomes Brian Goodwin Joshua Greene Dirk ter Haar Jacques Hadamard Mark Hadley Patrick Haggard J. B. S. Haldane Stuart Hameroff Augustin Hamon Sam Harris Ralph Hartley Hyman Hartman Jeff Hawkins John-Dylan Haynes Donald Hebb Martin Heisenberg Werner Heisenberg Grete Hermann John Herschel Basil Hiley Art Hobson Jesper Hoffmeyer Don Howard John H. Jackson William Stanley Jevons Roman Jakobson E. T. Jaynes Pascual Jordan Eric Kandel Ruth E. Kastner Stuart Kauffman Martin J. Klein William R. Klemm Christof Koch Simon Kochen Hans Kornhuber Stephen Kosslyn Daniel Koshland Ladislav Kovàč Leopold Kronecker Rolf Landauer Alfred Landé Pierre-Simon Laplace Karl Lashley David Layzer Joseph LeDoux Gerald Lettvin Gilbert Lewis Benjamin Libet David Lindley Seth Lloyd Werner Loewenstein Hendrik Lorentz Josef Loschmidt Alfred Lotka Ernst Mach Donald MacKay Henry Margenau Owen Maroney David Marr Humberto Maturana James Clerk Maxwell Ernst Mayr John McCarthy Warren McCulloch N. David Mermin George Miller Stanley Miller Ulrich Mohrhoff Jacques Monod Vernon Mountcastle Emmy Noether Donald Norman Travis Norsen Alexander Oparin Abraham Pais Howard Pattee Wolfgang Pauli Massimo Pauri Wilder Penfield Roger Penrose Steven Pinker Colin Pittendrigh Walter Pitts Max Planck Susan Pockett Henri Poincaré Daniel Pollen Ilya Prigogine Hans Primas Zenon Pylyshyn Henry Quastler Adolphe Quételet Pasco Rakic Nicolas Rashevsky Lord Rayleigh Frederick Reif Jürgen Renn Giacomo Rizzolati A.A. Roback Emil Roduner Juan Roederer Jerome Rothstein David Ruelle David Rumelhart Robert Sapolsky Tilman Sauer Ferdinand de Saussure Jürgen Schmidhuber Erwin Schrödinger Aaron Schurger Sebastian Seung Thomas Sebeok Franco Selleri Claude Shannon Charles Sherrington Abner Shimony Herbert Simon Dean Keith Simonton Edmund Sinnott B. F. Skinner Lee Smolin Ray Solomonoff Roger Sperry John Stachel Henry Stapp Tom Stonier Antoine Suarez Leo Szilard Max Tegmark Teilhard de Chardin Libb Thims William Thomson (Kelvin) Richard Tolman Giulio Tononi Peter Tse Alan Turing C. S. Unnikrishnan Nico van Kampen Francisco Varela Vlatko Vedral Vladimir Vernadsky Mikhail Volkenstein Heinz von Foerster Richard von Mises John von Neumann Jakob von Uexküll C. H. Waddington James D. Watson John B. Watson Daniel Wegner Steven Weinberg Paul A. Weiss Herman Weyl John Wheeler Jeffrey Wicken Wilhelm Wien Norbert Wiener Eugene Wigner E. O. Wilson Günther Witzany Stephen Wolfram H. Dieter Zeh Semir Zeki Ernst Zermelo Wojciech Zurek Konrad Zuse Fritz Zwicky Presentations Biosemiotics Free Will Mental Causation James Symposium |
The Measurement Problem
The "Problem of Measurement" in quantum mechanics has been defined in various ways, originally by physicists, and more recently by philosophers of physics who question the "foundations of quantum mechanics." Inspired by Albert Einstein, they seek a more "realistic" explanation of what is going on, one that lets us "visualize" quantum processes in the familiar causal terms in our everyday experiences that can explain classical mechanics
Richard Feynman famously cautioned against looking for such "realistic" visualizations, saying that we cannot "understand" quantum mechanics in terms of a familiar "mechanism." He says "there is no mechanism," leaving us with what he called the one and only mystery of quantum mechanics."
Many physicists define the "problem" of measurement simply as the logical contradiction between two "laws" (one quantum random, the other classically certain ) that appear to contradict one another when describing the motion or "evolution" in space and time of a quantum system.
The first motion "law" is the irreversible, non-unitary, discrete, discontinuous, and indeterministic or "random" collapse of the wave function. P.A.M.Dirac called it his Projection Postulate. A few years later John von Neumann called this Process 1. At the moment of this "collapse" new information appears in the universe. It is this information that is the "outcome" of a measurement. Werner Heisenberg saw this law as "acausal" and "statistical."
The second motion "law" is the time reversible, unitary, continuous, and deterministic evolution of the Schrödinger equation (von Neumann's Process 2). Nothing observable happens during this motion. No new information appears that might be observed.
John von Neumann was perhaps first to see a logical problem with these two distinct (indeed, opposing) processes. Later physicists saw no mechanism that can explain the transition from a continuous evolution to the discontinuous state change. The standard formalism of quantum mechanics says that the deterministic continuous evolution "law" describes only the probability of the indeterministic "collapse" of the second "law."
Max Born summarized this conflict as a paradox: "The motion of the particle follows the laws of probability, but the probability itself propagates in accord with causal laws."
The mathematical formalism of quantum mechanics simply provides no way to predict when the wave function stops evolving in a predictable deterministic fashion and indeterministicallycollapses randomly and unpredictably.
Starting with Von Neumann, physicists have claimed that the collapse must occur when a microscopic quantum system interacts with a macroscopic (approximately classical) measuring apparatus. The apparatus "measures" the quantum system and the wave-function "collapses," producing the irreversible information that can at a later time be seen by an observer.
But we must note that this classical measurement apparatus has been only an ad hoc assumption that has never produced a model or mechanism of its inner workings.
Some theorists have added ad hoc non-linear terms to the Schrödinger equation to force the collapse. But these extra terms still do not predict the time of the collapse exactly, nor do they describe what is happening during the collapse process.
So ultimately, the collapse happens at a random time and at that time macroscopically observable new information appears irreversibly, as first claimed by von Neumann.
To describe the problem of measurement more fully we need diverse concepts in quantum physics such as:
How Classical Is a Macroscopic Measuring Apparatus?
As Landau and Lifshitz described it in their 1958 textbook Quantum Mechanics"
The possibility of a quantitative description of the motion of an electron requires the presence also of physical objects which obey classical mechanics to a sufficient degree of accuracy. If an electron interacts with such a "classical object", the state of the latter is, generally speaking, altered. The nature and magnitude of this change depend on the state of the electron, and therefore may serve to characterise it quantitatively... We have defined "apparatus" as a physical object which is governed, with sufficient accuracy, by classical mechanics. Such, for instance, is a body of large enough mass. However, it must not be supposed that apparatus is necessarily macroscopic. Under certain conditions, the part of apparatus may also be taken by an object which is microscopic, since the idea of "with sufficient accuracy" depends on the actual problem proposed. Thus quantum mechanics occupies a very unusual place among physical theories: it contains classical mechanics as a limiting case [correspondence principle], yet at the same time it requires this limiting case for its own formulation.The measurement problem was analyzed mathematically in 1932 by John von Neumann. Following the work of Niels Bohr and Werner Heisenberg, von Neumann divided the world into a microscopic (atomic-level) quantum system and a macroscopic (classical) measuring apparatus. Von Neumann explained that two fundamentally different processes are going on in quantum mechanics.
Process 3 - a conscious observer recording new information in a mind. This is only possible if there are two local reductions in the entropy (the first in the measurement apparatus, the second in the mind), both balanced by even greater increases in positive entropy that must be transported away from the apparatus and the mind, so the overall increase in entropy can satisfy the second law of thermodynamics. For some physicists, it is the wave-function collapse that gives rise to the problem of measurement because its randomness prevents us from including it in the mathematical formalism of the deterministic Schrödinger equation in process 2. The randomness that is irreducibly involved in all information creation lies at the heart of human freedom. It is the "free" in "free will." The "will" part is as adequately and statistically determined as any macroscopic object.
Designing a Quantum Measurement Apparatus
The first step is to build an apparatus that allows different components of the wave function to evolve along distinguishable paths into different regions of space, where the different regions correspond to (are correlated with) the physical properties we want to measure. We then can locate a detector in these different regions of space to catch particles travelling a particular path.
We do not say that the system is on a particular path in this first step. That would cause the probability amplitude wave function to collapse. This first step is reversible, at least in principle. It is deterministic and an example of von Neumann process 2.
Let's consider the separation of a beam of photons into horizontally and vertically polarized photons by a birefringent crystal.
We need a beam of photons (and the ability to reduce the intensity to a single photon at a time). Vertically polarized photons pass straight through the crystal. They are called the ordinary ray, shown in red. Horizontally polarized photons, however, are deflected at an angle up through the crystal, then exit the crystal back at the original angle. They are called the extraordinary ray, shown in blue.
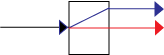
| ψ > = ( 1/√2) | h > + ( 1/√2) | v > (1)See the Dirac Three Polarizers experiment for more details on polarized photons.
An Information-Preserving, Reversible Example of Process 2
To show that process 2 is reversible, we can add a second birefringent crystal upside down from the first, but inline with the superposition of physically separated states,

An Information-Creating, Irreversible Example of Process 1
But now suppose we insert something between the two crystals that is capable of a measurement to produce observable information. We need a detector that locates the photon in one of the two rays.
We can now create an information-creating, irreversible example of process 1. Suppose we insert something between the two crystals that is capable of a measurement to produce observable information. We need detectors, for example two charge-coupled devices that locate the photon in one of the two rays.
We can write a quantum description of the CCDs, one measuring horizontal photons, | Ah > (shown as the blue spot), and the other measuring vertical photons, | Av > (shown as the red spot).
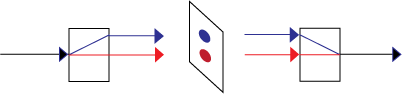
| ψ > + | Ah0 > => | ψ, Ah0 > => | h, Ah1 >These jumps destroy (unobservable) phase information, raise the (Boltzmann) entropy of the apparatus, and increase visible information (Shannon entropy) in the form of the visible spot. The entropy increase takes the form of a large chemical energy release when the photographic spot is developed (or a cascade of electrons in a CCD). Note that the birefringent crystal and the parts of the macroscopic apparatus other than the sensitive detectors are treated classically. We can animate these irreversible and reversible processes, 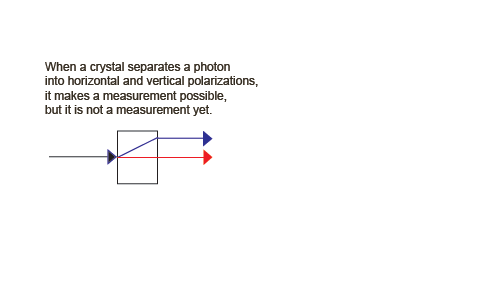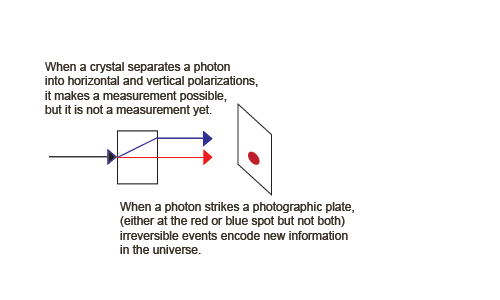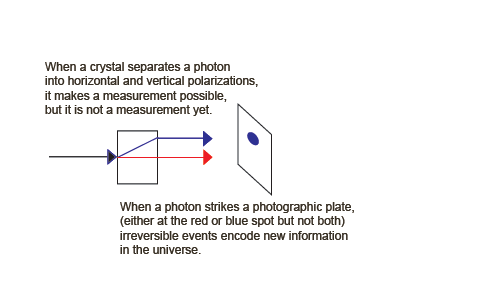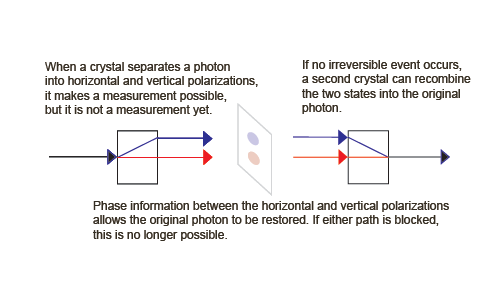
The Boundary between the Classical and Quantum Worlds
Some scientists (John von Neumann and Eugene Wigner, for example) have argued that in the absence of a conscious observer, or some "cut" between the microscopic and macroscopic world, the evolution of the quantum system and the macroscopic measuring apparatus would be described deterministically by Schrödinger's equation of motion for the wave function | ψ + A > with the Hamiltonian H energy operator,
Our quantum mechanical analysis of the measurement apparatus in the above case allows us to locate the "cut" or "Schnitt" between the microscopic and macroscopic world at those components of the "adequately classical and deterministic" apparatus that put the apparatus in an irreversible stable state providing new information to the observer. John Bell drew a diagram to show the various possible locations for what he called the "shifty split." Information physics shows us that the correct location for the boundary is the first of Bell's possibilities.
The Role of a Conscious Observer
In 1941, Carl von Weizsäcker described the measurement problem as an interaction between a Subject and an Object, a view shared by the philosopher of science Ernst Cassirer.
Fritz London and Edmond Bauer made the strongest case for the critical role of a conscious observer in 1939:
So far we have only coupled one apparatus with one object. But a coupling, even with a measuring device, is not yet a measurement. A measurement is achieved only when the position of the pointer has been observed. It is precisely this increase of knowledge, acquired by observation, that gives the observer the right to choose among the different components of the mixture predicted by theory, to reject those which are not observed, and to attribute thenceforth to the object a new wave function, that of the pure case which he has found. We note the essential role played by the consciousness of the observer in this transition from the mixture to the pure case. Without his effective intervention, one would never obtain a new function.In 1961, Eugene Wigner made quantum physics even more subjective, claiming that a quantum measurement requires a conscious observer, without which nothing ever happens in the universe. When the province of physical theory was extended to encompass microscopic phenomena, through the creation of quantum mechanics, the concept of consciousness came to the fore again: it was not possible to formulate the laws of quantum mechanics in a fully consistent way without reference to the consciousness All that quantum mechanics purports to provide are probability connections between subsequent impressions (also called "apperceptions") of the consciousness, and even though the dividing line between the observer, whose consciousness is being affected, and the observed physical object can be shifted towards the one or the other to a considerable degree [cf., von Neumann] it cannot be eliminated. It may be premature to believe that the present philosophy of quantum mechanics will remain a permanent feature of future physical theories; it will remain remarkable, in whatever way our future concepts may develop, that the very study of the external world led to the conclusion that the content of the consciousness is an ultimate reality.Other physicists were more circumspect. Niels Bohr contrasted Paul Dirac's view with that of Heisenberg: These problems were instructively commented upon from different sides at the Solvay meeting, in the same session where Einstein raised his general objections. On that occasion an interesting discussion arose also about how to speak of the appearance of phenomena for which only predictions of statistical character can be made. The question was whether, as to the occurrence of individual effects, we should adopt a terminology proposed by Dirac, that we were concerned with a choice on the part of "nature," or, as suggested by Heisenberg, we should say that we have to do with a choice on the part of the "observer" constructing the measuring instruments and reading their recording. Any such terminology would, however, appear dubious since, on the one hand, it is hardly reasonable to endow nature with volition in the ordinary sense, while, on the other hand, it is certainly not possible for the observer to influence the events which may appear under the conditions he has arranged. To my mind, there is no other alternative than to admit that, in this field of experience, we are dealing with individual phenomena and that our possibilities of handling the measuring instruments allow us only to make a choice between the different complementary types of phenomena we want to study.Landau and Lifshitz said clearly that quantum physics was independent of any observer: In this connection the "classical object" is usually called apparatus, and its interaction with the electron is spoken of as measurement. However, it must be most decidedly emphasised that we are here not discussing a process of measurement in which the physicist-observer takes part. By measurement, in quantum mechanics, we understand any process of interaction between classical and quantum objects, occurring apart from and independently of any observer.David Bohm agreed that what is observed is distinct from the observer: If it were necessary to give all parts of the world a completely quantum-mechanical description, a person trying to apply quantum theory to the process of observation would be faced with an insoluble paradox. This would be so because he would then have to regard himself as something connected inseparably with the rest of the world. On the other hand,the very idea of making an observation implies that what is observed is totally distinct from the person observing it.And John Bell said: It would seem that the [quantum] theory is exclusively concerned about 'results of measurement', and has nothing to say about anything else. What exactly qualifies some physical systems to play the role of 'measurer'? Was the wavefunction of the world waiting to jump for thousands of millions of years until a single-celled living creature appeared? Or did it have to wait a little longer, for some better qualified system...with a Ph.D.? If the theory is to apply to anything but highly idealised laboratory operations, are we not obliged to admit that more or less 'measurement-like' processes are going on more or less all the time, more or less everywhere? Do we not have jumping then all the time?
Three Essential Steps in a "Measurement" and "Observation"
We can distinguish three required elements in a measurement that can clarify the ongoing debate about the role of a conscious observer.
For Teachers
For Scholars
John Bell on Measurement
It would seem that the [quantum] theory is exclusively concerned about 'results of measurement', and has nothing to say about anything else. What exactly qualifies some physical systems to play the role of 'measurer'? Was the wavefunction of the world waiting to jump for thousands of millions of years until a single-celled living creature appeared? Or did it have to wait a little longer, for some better qualified system...with a Ph.D.? If the theory is to apply to anything but highly idealised laboratory operations, are we not obliged to admit that more or less 'measurement-like' processes are going on more or less all the time, more or less everywhere? Do we not have jumping then all the time?
Does [the 'collapse of the wavefunction'] happen sometimes outside laboratories? Or only in some authorized 'measuring apparatus'? And whereabouts in that apparatus? In the Einstein—Podolsky-Rosen—Bohm experiment, does 'measurement' occur already in the polarizers, or only in the counters? Or does it occur still later, in the computer collecting the data, or only in the eye, or even perhaps only in the brain, or at the brain—mind interface of the experimenter?
David Bohm on Measurement
In his 1950 textbook Quantum Theory, Bohm discusses measurement in chapter 22, section 12.
John von Neumann on Measurement
In his 1932 Mathematical Foundations of Quantum Mechanics (in German, English edition 1955) John von Neumann explained that two fundamentally different processes are going on in quantum mechanics.
It gave rise to the so-called problem of measurement because its randomness prevents it from being a part of the deterministic mathematics of process 2. Information physics has solved the problem of measurement by identifying the moment and place of the collapse of the wave function with the creation of an observable information structure. The presence of a conscious observer is not necessary. It is enough that the new information created is observable, should a human observer try to look at it in the future. Information physics is thus subtly involved in the question of what humans can know (epistemology).The Schnitt
von Neumann described the collapse of the wave function as requiring a "cut" (Schnitt in German) between the microscopic quantum system and the observer. He said it did not matter where this cut was placed, because the mathematics would produce the same experimental results.
There has been a lot of controversy and confusion about this cut. Some have placed it outside a room which includes the measuring apparatus and an observer A, and just before observer B makes a measurement of the physical state of the room, which is imagined to evolve deterministically according to process 2 and the Schrödinger equation.
The case of Schrödinger's Cat is thought to present a similar paradoxical problem.
von Neumann contributed a lot to this confusion in his discussion of subjective perceptions and "psycho-physical parallelism, which was encouraged by Neils Bohr. Bohr interpreted his "complementarity principle" as explaining the difference between subjectivity and objectivity (as well as several other dualisms). von Neumann wrote:
The difference between these two processes is a very fundamental one: aside from the different behaviors in regard to the principle of causality, they are also different in that the former is (thermodynamically) reversible, while the latter is not. Let us now compare these circumstances with those which actually exist in nature or in its observation. First, it is inherently entirely correct that the measurement or the related process of the subjective perception is a new entity relative to the physical environment and is not reducible to the latter. Indeed, subjective perception leads us into the intellectual inner life of the individual, which is extra-observational by its very nature (since it must be taken for granted by any conceivable observation or experiment). Nevertheless, it is a fundamental requirement of the scientific viewpoint -- the so-called principle of the psycho-physical parallelism -- that it must be possible so to describe the extra-physical process of the subjective perception as if it were in reality in the physical world -- i.e., to assign to its parts equivalent physical processes in the objective environment, in ordinary space. (Of course, in this correlating procedure there arises the frequent necessity of localizing some of these processes at points which lie within the portion of space occupied by our own bodies. But this does not alter the fact of their belonging to the "world about us," the objective environment referred to above.) In a simple example, these concepts might be applied about as follows: We wish to measure a temperature. If we want, we can pursue this process numerically until we have the temperature of the environment of the mercury container of the thermometer, and then say: this temperature is measured by the thermometer. But we can carry the calculation further, and from the properties of the mercury, which can be explained in kinetic and molecular terms, we can calculate its heating, expansion, and the resultant length of the mercury column, and then say: this length is seen by the observer. Going still further, and taking the light source into consideration, we could find out the reflection of the light quanta on the opaque mercury column, and the path of the remaining light quanta into the eye of the observer, their refraction in the eye lens, and the formation of an image on the retina, and then we would say: this image is registered by the retina of the observer. And were our physiological knowledge more precise than it is today, we could go still further, tracing the chemical reactions which produce the impression of this image on the retina, in the optic nerve tract and in the brain, and then in the end say: these chemical changes of his brain cells are perceived by the observer. But in any case, no matter how far we calculate -- to the mercury vessel, to the scale of the thermometer, to the retina, or into the brain, at some time we must say: and this is perceived by the observer. That is, we must always divide the world into two parts, the one being the observed system, the other the observer. In the former, we can follow up all physical processes (in principle at least) arbitrarily precisely. In the latter, this is meaningless.
Quantum Mechanics, by Albert Messiah, on Measurement
Messiah says a detailed study of the mechanism of measurement will not be made in his book, but he does say this.
The dynamical state of such a system is represented at a given instant of time by its wave function at that instant. The causal relationship between the wave function γ(to) at an initial time to, and the wave function γ(t) at any later time, is expressed through the Schrödinger equation. However, as soon as it is subjected to observation, the system experiences some reaction from the observing instrument. Moreover, the above reaction is to some extent unpredictable and uncontrollable since there is no sharp separation between the observed system and the observing instrument. They must be treated as an indivisible quantum system whose wave function Ψ(t) depends upon the coordinates of the measuring device as well as upon those of the observed system. During the process of observation, the measured system can no longer be considered separately and the very notion of a dynamical state defined by the simpler wave function γ(t) loses its meaning. Thus the intervention of the observing instrument destroys all causal connection between the state of the system before and after the measurement; this explains why one cannot in general predict with certainty in what state the system will be found after the measurement; one can only make predictions of a statistical nature1.1) The statistical predictions concerning the results of measurement are derived very naturally from the study of the mechanism of the measuring operation itself, a study in which the measuring instrument is treated as a quantized object and the complex (system + measuring instrument) evolves in causal fashion in accordance with the Schrödinger equation. A very concise and simple presentation of the measuring process in Quantum Mechanics is given. in F. London and E. Bauer, La Théorie de l'Observation en Mécanique Quantique (Paris, Hermann, 1939). More detailed discussions of this problem may be found in J. von Neumann, Mathematical Foundations of Quantum Mechanics (Princeton, Princeton University Press, 1955), and in D. Bohm, (Quantum Theory New York, Prentice-Hall, 1951).
Decoherence Theorists on Measurement
In general, decoherence theorists see the problem of measurement as why do we not see macroscopic superpositions of states. Why do measurements always show a system and its measuring apparatus to be in a particular state - a "pointer state," and not in a superposition?
Our answer is that we never see microscopic systems in a superposition of states either. Dirac's principle of superposition says only that the probability (amplitudes) of finding a system in different states has non-zero values for different states. Measurements always reveal a system to be in one state. Which state is found is a matter of chance. [Decoherence theorists do not like this indeterminism.] The statistics from large numbers of measurements of identically prepared systems verify the predicted probabilities for the different states. The accuracy of these quantum mechanical predictions (1 part in 1015) shows quantum mechanics to be the most accurate theory ever known.
Guido Bacciagaluppi summarized the view of decoherence theorists in an article for the Stanford Encyclopedia of Philosophy. He defines the measurement problem as the lack of macroscopic superpositions:
The measurement problem, in a nutshell, runs as follows. Quantum mechanical systems are described by wave-like mathematical objects (vectors) of which sums (superpositions) can be formed (see the entry on quantum mechanics). Time evolution (the Schrödinger equation) preserves such sums. Thus, if a quantum mechanical system (say, an electron) is described by a superposition of two given states, say, spin in x-direction equal +1/2 and spin in x-direction equal -1/2, and we let it interact with a measuring apparatus that couples to these states, the final quantum state of the composite will be a sum of two components [that is to say, a macroscopic superposition, which is of course never seen!], one in which the apparatus has coupled to (has registered) x-spin = +1/2, and one in which the apparatus has coupled to (has registered) x-spin = -1/2... [D]ecoherence as such does not provide a solution to the measurement problem, at least not unless it is combined with an appropriate interpretation of the theory (whether this be one that attempts to solve the measurement problem, such as Bohm, Everett or GRW; or one that attempts to dissolve it, such as various versions of the Copenhagen interpretation). Some of the main workers in the field such as Zeh (2000) and (perhaps) Zurek (1998) suggest that decoherence is most naturally understood in terms of Everett-like interpretations.Maximilian Schlosshauer situates the problem of measurement in the context of the so-called "quantum-to-classical transition," namely the question of exactly how deterministic classical behavior emerges from the indeterministic microscopic quantum world. In this section, we shall describe the (in)famous measurement problem of quantum mechanics that we have already referred to in several places in the text. The choice of the term "measurement problem" has purely historical reasons: Certain foundational issues associated with the measurement problem were first illustrated in the context of a quantum-mechanical description of a measuring apparatus interacting with a system. However, one may regard the term "measurement problem" as implying too narrow a scope, chiefly for the following two reasons. First, as we shall see below, the measurement problem is composed of three distinct issues, so it would make sense to rather speak of measurement problems. Second, quantum measurement and the arising foundational problems are but a special case of the more general problem of the quantum-to-classical transition, i.e., the question of how effectively classical systems and properties around us emerge from the underlying quantum domain. On the one hand, then, the problem of the quantum-to-classical transition has a much broader scope than the issue of quantum measurement in the literal sense. On the other hand, however, many interactions between physical systems can be viewed as measurement-like interactions. For example, light scattering off an object carries away information about the position of the object, and it is in this sense that we thus may view these incident photons as a "measuring device." Such ubiquitous measurement-like interactions lie at the heart of the explanation of the quantum-to-classical transition by means of decoherence. Measurement, in the more general sense, thus retains its paramount importance also in the broader context of the quantum-to-classical transition, which in turn motivates us not to abandon the term "measurement problem" altogether in favor of the more general "problem of the quantum-to-classical transition." As indicated above, the measurement problem (and the problem of the quantum-to-classical transition) is composed of three parts, all of which we shall describe in more detail in the following:The main concern of the decoherence theorists then is to recover a deterministic picture of quantum mechanics that would allow them to predict the outcome of a particular experiment. They have what William James called an "antipathy to chance." Max Tegmark and John Wheeler made this clear in a 2001 article in Scientific American:1. The problem of the preferred basis (Sect. 2.5.2). What singles out the preferred physical quantities in nature—e.g., why are physical systems usually observed to be in definite positions rather than in superpositions of positions? 2. The problem of the nonobservability of interference (Sect. 2.5.3). Why is it so difficult to observe quantum interference effects, especially on macroscopic scales? 3. The problem of outcomes (Sect. 2.5.4). Why do measurements have outcomes at all, and what selects a particular outcome among the different possibilities described by the quantum probability distribution? [The answer (since Einstein, 1916) is chance.]Familiarity with these problems will turn out to be important for a proper understanding of the scope, achievements, and implications of decoherence. To anticipate, it is fair to conclude that decoherence has essentially resolved the first two problems. Since these problems and their resolution can be formulated in purely operational terms within the standard formalism of quantum mechanics, the role played by decoherence in addressing these two issues is rather undisputed. By contrast, the success of decoherence in tackling the third issue — the problem of outcomes — remains a matter of debate, in particular, because this issue is almost inextricably linked to the choice of a specific interpretation of quantum mechanics (which mostly boils down to a matter of personal preference). In fact, most of the overly optimistic or pessimistic statements about the ability of decoherence to solve "the" measurement problem can be traced back to a misunderstanding of the scope that a standard quantum effect such as decoherence may have in resolving the more interpretive problem of outcomes. The discovery of decoherence, combined with the ever more elaborate experimental demonstrations of quantum weirdness, has caused a noticeable shift in the views of physicists. The main motivation for introducing the notion of wave-function collapse had been to explain why experiments produced specific outcomes and not strange superpositions of outcomes. Now much of that motivation is gone. Moreover, it is embarrassing that nobody has provided a testable deterministic equation specifying precisely when the mysterious collapse is supposed to occur.H. Dieter Zeh, the founder of the "decoherence program," defines the measurement problem as a macroscopic entangled superposition of all possible measurement outcomes: Because of the dynamical superposition principle, an initial superposition Σ cn | n > does not lead to definite pointer positions (with their empirically observed frequencies). If decoherence is neglected, one obtains their entangled superposition Σ cn | n > | Ψ n >, that is, a state that is different from all potential measurement outcomes | n > | Ψ n >. This dilemma represents the "quantum measurement problem" to be discussed in Sect. 2.3. Von Neumann's interaction is nonetheless regarded as the first step of a measurement (a "pre-measurement"). Yet, a collapse seems still to be required - now in the measurement device rather than in the microscopic system. Because of the entanglement between system and apparatus, it would then affect the total system.Zeh continues: It's not clear why the standard ensemble interpretation is "ruled out," but Zeh offers a solution, which is to deny the projection postulate of standard quantum mechanics and use an unconventional interpretation that makes wave-function collapses only "apparent": A way out of this dilemma within quantum mechanical concepts requires one of two possibilities: a modification of the Schrodinger equation that explicitly describes a collapse (also called "spontaneous localization" - see Chap. 8), or an Everett type interpretation, in which all measurement outcomes are assumed to exist in one formal superposition, but to be perceived separately as a consequence of their dynamical autonomy resulting from decoherence. While this latter suggestion has been called "extravagant" (as it requires myriads of co-existing quasi-classical "worlds"), it is similar in principle to the conventional (though nontrivial) assumption, made tacitly in all classical descriptions of observation, that consciousness is localized in certain semi-stable and sufficiently complex subsystems (such as human brains or parts thereof) of a much larger external world.Jeffrey Bub worked with David Bohm to develop Bohm's theory of "hidden variables." They hoped their theory might provide a deterministic basis for quantum theory and support Albert Einstein's view of a physical world independent of observations of the world. The standard theory of quantum mechanics is irreducibly statistical and indeterministic, a consequence of the collapse of the wave function when many possibilities for physical outcomes of an experiment reduce to a single actual outcome. This is a book about the interpretation of quantum mechanics, and about the measurement problem. The conceptual entanglements of the measurement problem have their source in the orthodox interpretation of 'entangled' states that arise in quantum mechanical measurement processes... All standard treatments of quantum mechanics take an observable as having a determinate value if the quantum state is an eigenstate of that observable. If the state is not an eigenstate of the observable, no determinate value is attributed to the observable. This principle - sometimes called the 'eigenvalue-eigenstate link' - is explicitly endorsed by Dirac (1958, pp. 46-7) and von Neumann (1955, p. 253), and clearly identified as the 'usual' view by Einstein, Podolsky, and Rosen (1935) in their classic argument for the incompleteness of quantum mechanics (see chapter 2). Since the dynamics of quantum mechanics described by Schrödinger's time-dependent equation of motion is linear, it follows immediately from this orthodox interpretation principle that, after an interaction between two quantum mechanical systems that can be interpreted as a measurement by one system on the other, the state of the composite system is not an eigenstate of the observable measured in the interaction, and not an eigenstate of the indicator observable functioning as a 'pointer.' So, on the orthodox interpretation, neither the measured observable nor the pointer reading have determinate values, after a suitable interaction that correlates pointer readings with values of the measured observable. This is the measurement problem of quantum mechanics. References
Bacciagaluppi, Guido, The Role of Decoherence in Quantum Mechanics, first published Mon Nov 3, 2003; substantive revision Mon Apr 16, 2012
Jeffrey Bub, Interpreting the Quantum World. Cambridge University, 1997, p.2.
Adriana Daneri, A. Loinger, and G. M. Prosperi, Nuclear Physics, 33 (1962) pp.297-319. (W&Z, p.657)
Erich Joos, H. Dieter Zeh, et al., Decoherence and the Appearance of a Classical World in Quantum Theory. Springer, 2010,
Gunter Ludwig, Zeitschrift für Physik, 135 (1953) p.483
Maximilian Schlosshauer, Decoherence and the Quantum-to-Classical Transition. Springer, 2007, pp.49-50
Leo Szilard, Behavioral Science, 9 (1964) pp.301-10. (W&Z, p.539)
Max Tegmark and John Wheeler, Scientific American, February (2001) pp.68-75.
John von Neumann, The Mathematical Foundations of Quantum Mechanics, (Princeton, NJ, Princeton U. Press, 1955), pp.347-445. (W&Z, p.549)
John Wheeler and Wojciech Zurek, Quantum Theory and Measurement (Princeton, NJ, Princeton U. Press, 1983) (= W&Z)
Eugene Wigner, "The Problem of Measurement," Symmetries and Reflections (Bloomington, IN, Indiana U. Press, 1967) pp.153-70. (W&Z, p.324)
|