|
Philosophers
Mortimer Adler Rogers Albritton Alexander of Aphrodisias Samuel Alexander William Alston Anaximander G.E.M.Anscombe Anselm Louise Antony Thomas Aquinas Aristotle David Armstrong Harald Atmanspacher Robert Audi Augustine J.L.Austin A.J.Ayer Alexander Bain Mark Balaguer Jeffrey Barrett William Barrett William Belsham Henri Bergson George Berkeley Isaiah Berlin Richard J. Bernstein Bernard Berofsky Robert Bishop Max Black Susanne Bobzien Emil du Bois-Reymond Hilary Bok Laurence BonJour George Boole Émile Boutroux Daniel Boyd F.H.Bradley C.D.Broad Michael Burke Jeremy Butterfield Lawrence Cahoone C.A.Campbell Joseph Keim Campbell Rudolf Carnap Carneades Nancy Cartwright Gregg Caruso Ernst Cassirer David Chalmers Roderick Chisholm Chrysippus Cicero Tom Clark Randolph Clarke Samuel Clarke Anthony Collins Antonella Corradini Diodorus Cronus Jonathan Dancy Donald Davidson Mario De Caro Democritus Daniel Dennett Jacques Derrida René Descartes Richard Double Fred Dretske John Earman Laura Waddell Ekstrom Epictetus Epicurus Austin Farrer Herbert Feigl Arthur Fine John Martin Fischer Frederic Fitch Owen Flanagan Luciano Floridi Philippa Foot Alfred Fouilleé Harry Frankfurt Richard L. Franklin Bas van Fraassen Michael Frede Gottlob Frege Peter Geach Edmund Gettier Carl Ginet Alvin Goldman Gorgias Nicholas St. John Green H.Paul Grice Ian Hacking Ishtiyaque Haji Stuart Hampshire W.F.R.Hardie Sam Harris William Hasker R.M.Hare Georg W.F. Hegel Martin Heidegger Heraclitus R.E.Hobart Thomas Hobbes David Hodgson Shadsworth Hodgson Baron d'Holbach Ted Honderich Pamela Huby David Hume Ferenc Huoranszki Frank Jackson William James Lord Kames Robert Kane Immanuel Kant Tomis Kapitan Walter Kaufmann Jaegwon Kim William King Hilary Kornblith Christine Korsgaard Saul Kripke Thomas Kuhn Andrea Lavazza James Ladyman Christoph Lehner Keith Lehrer Gottfried Leibniz Jules Lequyer Leucippus Michael Levin Joseph Levine George Henry Lewes C.I.Lewis David Lewis Peter Lipton C. Lloyd Morgan John Locke Michael Lockwood Arthur O. Lovejoy E. Jonathan Lowe John R. Lucas Lucretius Alasdair MacIntyre Ruth Barcan Marcus Tim Maudlin James Martineau Nicholas Maxwell Storrs McCall Hugh McCann Colin McGinn Michael McKenna Brian McLaughlin John McTaggart Paul E. Meehl Uwe Meixner Alfred Mele Trenton Merricks John Stuart Mill Dickinson Miller G.E.Moore Ernest Nagel Thomas Nagel Otto Neurath Friedrich Nietzsche John Norton P.H.Nowell-Smith Robert Nozick William of Ockham Timothy O'Connor Parmenides David F. Pears Charles Sanders Peirce Derk Pereboom Steven Pinker U.T.Place Plato Karl Popper Porphyry Huw Price H.A.Prichard Protagoras Hilary Putnam Willard van Orman Quine Frank Ramsey Ayn Rand Michael Rea Thomas Reid Charles Renouvier Nicholas Rescher C.W.Rietdijk Richard Rorty Josiah Royce Bertrand Russell Paul Russell Gilbert Ryle Jean-Paul Sartre Kenneth Sayre T.M.Scanlon Moritz Schlick John Duns Scotus Arthur Schopenhauer John Searle Wilfrid Sellars David Shiang Alan Sidelle Ted Sider Henry Sidgwick Walter Sinnott-Armstrong Peter Slezak J.J.C.Smart Saul Smilansky Michael Smith Baruch Spinoza L. Susan Stebbing Isabelle Stengers George F. Stout Galen Strawson Peter Strawson Eleonore Stump Francisco Suárez Richard Taylor Kevin Timpe Mark Twain Peter Unger Peter van Inwagen Manuel Vargas John Venn Kadri Vihvelin Voltaire G.H. von Wright David Foster Wallace R. Jay Wallace W.G.Ward Ted Warfield Roy Weatherford C.F. von Weizsäcker William Whewell Alfred North Whitehead David Widerker David Wiggins Bernard Williams Timothy Williamson Ludwig Wittgenstein Susan Wolf Xenophon Scientists David Albert Michael Arbib Walter Baade Bernard Baars Jeffrey Bada Leslie Ballentine Marcello Barbieri Gregory Bateson Horace Barlow John S. Bell Mara Beller Charles Bennett Ludwig von Bertalanffy Susan Blackmore Margaret Boden David Bohm Niels Bohr Ludwig Boltzmann Emile Borel Max Born Satyendra Nath Bose Walther Bothe Jean Bricmont Hans Briegel Leon Brillouin Stephen Brush Henry Thomas Buckle S. H. Burbury Melvin Calvin Donald Campbell Sadi Carnot Anthony Cashmore Eric Chaisson Gregory Chaitin Jean-Pierre Changeux Rudolf Clausius Arthur Holly Compton John Conway Simon Conway-Morris Jerry Coyne John Cramer Francis Crick E. P. Culverwell Antonio Damasio Olivier Darrigol Charles Darwin Richard Dawkins Terrence Deacon Lüder Deecke Richard Dedekind Louis de Broglie Stanislas Dehaene Max Delbrück Abraham de Moivre Bernard d'Espagnat Paul Dirac Hans Driesch John Dupré John Eccles Arthur Stanley Eddington Gerald Edelman Paul Ehrenfest Manfred Eigen Albert Einstein George F. R. Ellis Hugh Everett, III Franz Exner Richard Feynman R. A. Fisher David Foster Joseph Fourier Philipp Frank Steven Frautschi Edward Fredkin Augustin-Jean Fresnel Benjamin Gal-Or Howard Gardner Lila Gatlin Michael Gazzaniga Nicholas Georgescu-Roegen GianCarlo Ghirardi J. Willard Gibbs James J. Gibson Nicolas Gisin Paul Glimcher Thomas Gold A. O. Gomes Brian Goodwin Joshua Greene Dirk ter Haar Jacques Hadamard Mark Hadley Patrick Haggard J. B. S. Haldane Stuart Hameroff Augustin Hamon Sam Harris Ralph Hartley Hyman Hartman Jeff Hawkins John-Dylan Haynes Donald Hebb Martin Heisenberg Werner Heisenberg Grete Hermann John Herschel Basil Hiley Art Hobson Jesper Hoffmeyer Don Howard John H. Jackson William Stanley Jevons Roman Jakobson E. T. Jaynes Pascual Jordan Eric Kandel Ruth E. Kastner Stuart Kauffman Martin J. Klein William R. Klemm Christof Koch Simon Kochen Hans Kornhuber Stephen Kosslyn Daniel Koshland Ladislav Kovàč Leopold Kronecker Rolf Landauer Alfred Landé Pierre-Simon Laplace Karl Lashley David Layzer Joseph LeDoux Gerald Lettvin Gilbert Lewis Benjamin Libet David Lindley Seth Lloyd Werner Loewenstein Hendrik Lorentz Josef Loschmidt Alfred Lotka Ernst Mach Donald MacKay Henry Margenau Owen Maroney David Marr Humberto Maturana James Clerk Maxwell Ernst Mayr John McCarthy Warren McCulloch N. David Mermin George Miller Stanley Miller Ulrich Mohrhoff Jacques Monod Vernon Mountcastle Emmy Noether Donald Norman Travis Norsen Alexander Oparin Abraham Pais Howard Pattee Wolfgang Pauli Massimo Pauri Wilder Penfield Roger Penrose Steven Pinker Colin Pittendrigh Walter Pitts Max Planck Susan Pockett Henri Poincaré Daniel Pollen Ilya Prigogine Hans Primas Zenon Pylyshyn Henry Quastler Adolphe Quételet Pasco Rakic Nicolas Rashevsky Lord Rayleigh Frederick Reif Jürgen Renn Giacomo Rizzolati A.A. Roback Emil Roduner Juan Roederer Jerome Rothstein David Ruelle David Rumelhart Robert Sapolsky Tilman Sauer Ferdinand de Saussure Jürgen Schmidhuber Erwin Schrödinger Aaron Schurger Sebastian Seung Thomas Sebeok Franco Selleri Claude Shannon Charles Sherrington Abner Shimony Herbert Simon Dean Keith Simonton Edmund Sinnott B. F. Skinner Lee Smolin Ray Solomonoff Roger Sperry John Stachel Henry Stapp Tom Stonier Antoine Suarez Leo Szilard Max Tegmark Teilhard de Chardin Libb Thims William Thomson (Kelvin) Richard Tolman Giulio Tononi Peter Tse Alan Turing C. S. Unnikrishnan Nico van Kampen Francisco Varela Vlatko Vedral Vladimir Vernadsky Mikhail Volkenstein Heinz von Foerster Richard von Mises John von Neumann Jakob von Uexküll C. H. Waddington James D. Watson John B. Watson Daniel Wegner Steven Weinberg Paul A. Weiss Herman Weyl John Wheeler Jeffrey Wicken Wilhelm Wien Norbert Wiener Eugene Wigner E. O. Wilson Günther Witzany Stephen Wolfram H. Dieter Zeh Semir Zeki Ernst Zermelo Wojciech Zurek Konrad Zuse Fritz Zwicky Presentations Biosemiotics Free Will Mental Causation James Symposium |
Leo Szilard
Leo Szilard is perhaps best known for patenting particle accelerators and nuclear reactions in the 1930's and then preparing a letter to President Roosevelt delivered by Albert Einstein urging the United States to develop atomic weapons.
But Szilard's great contribution to information philosophy is his connecting an increase in thermodynamic (Boltzmann) entropy with any increase in information (he called it order) that results from a measurement.
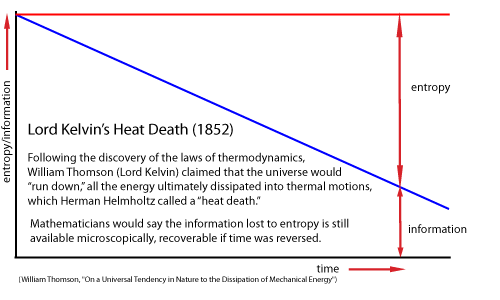
Many thinkers, beginning with William Thomson (Lord Kelvin) and Ludwig Boltzmann in the nineteenth century, had described any increase in entropy as simply a loss of oder and increase in disorder. Now Szilard showed that a gain in information/order in one place must also result in an increase in entropy/disorder in another place, to satisfy the second law of thermodynamics that overall entropy must always increase.
 Szilard quantitatively analyzed "Maxwell's Demon," the thought experiment suggested by James Clerk Maxwell, in which a reduction in entropy is possible when an intelligent being interacts with a thermodynamic system.
In the original Maxwell example, the demon measures the speed of molecules approaching a door between two volumes of gas. When fast molecules approach from the left, the demon opens the door to allow them into the right volume. When slow molecules approach from the right, he opens the door for them. The net result is a transfer of heat from left to right volumes, in apparent violation of the second law of thermodynamics.
Szilard considered the simplest possible steam engine, a cylinder with but a single molecule of gas. The cylinder is in contact with a heat reservoir to maintain isothermal conditions. Szilard's minimal intelligent demon inserts a partition into the middle of the cylinder and then notes whether the molecule is above or below the partition.
If the molecule is above, it can bounce against the partition and drive it down, doing work. The molecule loses energy (transferring momentum to the partition) but recovers its average energy from the infinite heat reservoir. If the molecule is below, it can drive the partition up. In either case, the demon can attach a weight to the partition to demonstrate its ability to do work, in apparent violation of the second law. Here is Szilard's description:
Szilard quantitatively analyzed "Maxwell's Demon," the thought experiment suggested by James Clerk Maxwell, in which a reduction in entropy is possible when an intelligent being interacts with a thermodynamic system.
In the original Maxwell example, the demon measures the speed of molecules approaching a door between two volumes of gas. When fast molecules approach from the left, the demon opens the door to allow them into the right volume. When slow molecules approach from the right, he opens the door for them. The net result is a transfer of heat from left to right volumes, in apparent violation of the second law of thermodynamics.
Szilard considered the simplest possible steam engine, a cylinder with but a single molecule of gas. The cylinder is in contact with a heat reservoir to maintain isothermal conditions. Szilard's minimal intelligent demon inserts a partition into the middle of the cylinder and then notes whether the molecule is above or below the partition.
If the molecule is above, it can bounce against the partition and drive it down, doing work. The molecule loses energy (transferring momentum to the partition) but recovers its average energy from the infinite heat reservoir. If the molecule is below, it can drive the partition up. In either case, the demon can attach a weight to the partition to demonstrate its ability to do work, in apparent violation of the second law. Here is Szilard's description:
A standing hollow cylinder, closed at both ends, can be separated into two possibly unequal sections of volumes V1 and V2 respectively by inserting a partition from the side at an arbitrarily fixed height. This partition forms a piston that can be moved up and down in the cylinder. An infinitely large heat reservoir of a given temperature T insures that any gas present in the cylinder undergoes isothermal expansion as the piston moves. This gas shall consist of a single molecule which, as long as the piston is not inserted into the cylinder, tumbles about in the whole cylinder by virtue of its thermal motion. Imagine, specifically, a man who at a given time inserts the piston into the cylinder and somehow notes whether the molecule is caught in the upper or lower part of the cylinder, that is, in volume V1 or V2. If he should find that the former is the case, then he would move the piston slowly downward until it reaches the bottom of the cylinder. During this slow movement of the piston the molecule stays, of course, above the piston. However, it is no longer constrained to the upper part of the cylinder but bounces many times against the piston which is already moving in the lower part of the cylinder. In this way the molecule does a certain amount of work on the piston. This is the work that corresponds to the isothermal expansion of an ideal gas - consisting of one single molecule from volume V1 to the volume V1 + V2. After some time, when the pistol has reached the bottom of the container, the molecule has again the full volume V to move about in, and the piston is then removed. The procedure can be repeated as many times as desired. The man moves the piston up or down depending on whether the molecule is trapped in the upper or lower half of the piston. In more detail, this motion may be caused by a weight, that is to be raised, through a mechanism that transmits the force from the piston to the weight, in such a way that the latter is always displaced upwards. In this way the potential energy of the weight certainly increases constantly. (The transmission of force to the weight is best arranged so that the force exerted by the weight on the piston at any position of the latter equals the average pressure of the gas.) It is clear that in this manner energy is constantly gained at the expense of heat, insofar as the biological phenomena of the intervening man are ignored in the calculation.Szilard argued that the intelligent being made a "measurement" of the molecule's position, stored that measurement's information in memory, and then used the information to attach the moving partition to a weight in order to get useful work. Because the measurement was a simple binary decision between the upper and lower volumes, Szilard anticipated the idea in Claude Shannon's information entropy that a single "bit" (a binary digit) of information was involved. Szilard calculated the mean value of the quantity of entropy produced by a 1-bit measurement as
S = k log 2,
where k is Boltzmann's constant. The base-2 logarithm reflects the binary decision.
The amount of entropy generated by the measurement may, of course, always be greater than this fundamental amount, but not smaller, or the second law would be violated.
Szilard connected the act of measurement to the acquisition of information, which was stored in the memory of the observer. This memory was then used to decide how to extract useful work. His discussion parallels in many respects the problem of measurement in quantum mechanics.
For brevity we shall talk about a "measurement," if we succeed in coupling the value of a parameter y. (for instance the position co-ordinate of a pointer of a measuring instrument) at one moment with the simultaneous value of a fluctuating parameter x of the system, in such a way that, from the value y, we can draw conclusions about the value that x had at the moment of the "measurement." Then let x and y be uncoupled after the measurement, so that x can change, while y retains its value for some time. Such measurements are not harmless interventions. A system in which such measurements occur shows a sort of memory faculty, in the sense that one can recognize by the state parameter y what value another state parameter x had at an earlier moment, and we shall see that simply because of such a memory the Second Law would be violated, if the measurement could take place without compensation. We shall realize that the Second Law is not threatened as much by this entropy decrease as one would think, as soon as we see that the entropy decrease resulting from the intervention would be compensated completely in any event if the execution of such a measurement were, for instance, always accompanied by production of k log 2 units of entropy. In that case it will be possible to find a more general entropy law, which applies universally to all measurements.Although Szilard's fundamental relation between the information gained in all measurements and the necessary increase in entropy has been studied by many scientists, including Leon Brillouin, Gunter Ludwig, Norbert Wiener, Rolf Landauer, Charles Bennett, and Wojciech Zurek, it has never been seriously challenged - although some information theorists would like to limit information as meaningful messages between a sender and a receiver (Bernd-Olaf Kuppers, Juan Roederer), the theory of the communication of information has never included meaning or purpose. Information physics takes the Szilard relation one step further and identifies the moment that information is encoded stably in the universe as the von Neumann/Heisenberg "cut" between the microscopic quantum world and the macroscopic classical world.
References
On the Decrease in Entropy in a Thermodynamic System by the Intervention of Intelligent Beings
For Teachers
For Scholars
ON THE DECREASE OF ENTROPY IN A THERMODYNAMIC SYSTEM BY THE INTERVENTION OF INTELLIGENT BEINGS
The objective of the investigation is to find the conditions which apparently allow the construction of a perpetual-motion machine of the second kind, if one permits an intelligent being to intervene in a thermodynamic system. When such beings make measurements, they make the system behave in a manner distinctly different from the way a mechanical system behaves when left to itself. We show that it is a sort of a memory faculty, manifested by a system where measurements occur, that might cause a permanent decrease of entropy and thus a violation of the Second Law of Thermodynamics, were it not for the fact that the measurements themselves are necessarily accompanied by a production of entropy. At first we calculate this production of entropy quite generally from the postulate that full compensation is made in the sense of the Second Law (Equation [1]). Second, by using an inanimate device able to make measurements — however under continual entropy production — we shall calculate the resulting quantity of entropy. We find that it is exactly as great as is necessary for full compensation. The actual production of entropy in connection with the measurement, therefore, need not be greater than Equation (1) requires.
There is an objection, already historical, against the universal validity of the Second Law of Thermodynamics, which indeed looks rather ominous. The objection is embodied in the notion of Maxwell's demon, who in a different form appears even nowadays again and again; perhaps not unreasonably, inasmuch as behind the precisely formulated question quantitative connections seem to be hidden which to date have not been clarified. The objection in its original formulation concerns a demon who catches the fast molecules and lets the slow ones pass. To be sure, the objection can be met with the reply that man cannot in principle foresee the value of a thermally fluctuating parameter. However, one cannot deny that we can very well measure the value of such a fluctuating parameter and therefore could certainly gain energy at the expense of heat by arranging our intervention according to the results of the measurements. Presently, of course, we do not know whether we commit an error by not including the intervening man into the system and by disregarding his biological phenomena.
Apart from this unresolved matter, it is known today that in a system left to itself no "perpetuum mobile" (perpetual motion machine) of the second kind (more exactly, no "automatic machine of continual finite work-yield which uses heat at the lowest temperature") can operate in spite of the fluctuation phenomena. A perpetuum mobile would have to be a machine which in the long run could lift a weight at the expense of the heat content of a reservoir. In other words, if we want to use the fluctuation phenomena in order to gain energy at the expense of heat, we are in the same position as playing a game of chance, in which we may win certain amounts now and then, although the expectation value of the winnings is zero or negative. The same applies to a system where the intervention from outside is performed strictly periodically, say by periodically moving machines. We consider this as established (Szilard, 1925) and intend here only to consider the difficulties that occur when intelligent beings intervene in a system. We shall try to discover the quantitative relations having to do with this intervention.
Smoluchowski (1914, p. 89) writes: "As far as we know today, there is no automatic, permanently effective perpetual motion machine, in spite of the molecular fluctuations, but such a device might, perhaps, function regularly if it were appropriately operated by intelligent beings...."
A perpetual motion machine therefore is possible if — according to the general method of physics — we view the experimenting man as a sort of deus ex machina, one who is continuously and exactly informed of the existing state of nature and who is able to start or interrupt the macroscopic course of nature at any moment without expenditure of work. Therefore he would definitely not have to possess the ability to catch single molecules like Maxwell's demon, although he would definitely be different from real living beings in possessing the above abilities. In eliciting any physical effect by action of the sensory
as well as the motor nervous systems a degradation of energy is always involved, quite apart from the fact that the very existence of a nervous system is dependent on continual dissipation of energy.
Whether - considering these circumstances - real living beings could continually or at least regularly produce energy at the expense of heat of the lowest temperature appears very doubtful, even though our ignorance of the biological phenomena does not allow a definite answer. However, the latter questions lead beyond the scope of physics in the strict sense.
It appears that the ignorance of the biological phenomena need not prevent us from understanding that which seems to us to be the essential thing. We may be sure that intelligent living beings — insofar as we are dealing with their intervention in a thermodynamic system — can be replaced by nonliving devices whose "biological phenomena" one could follow and determine whether in fact a compensation of the entropy decrease takes place as a result of the intervention by such a device in a system.
In the first place, we wish to learn what circumstance conditions the decrease of entropy which takes place when intelligent living beings intervene in a thermodynamic system. We shall see that this depends on a certain type of coupling between different parameters of the system. We shall consider an unusually simple type of these ominous couplings. For brevity we shall talk about a "measurement," if we succeed in coupling the value of a parameter y. (for instance the position co-ordinate of a pointer of a measuring instrument) at one moment with the simultaneous value of a fluctuating parameter x of the system, in such a way that, from the value y, we can draw conclusions about the value that x had at the moment of the "measurement." Then let x and y be uncoupled after the measurement, so that x can change, while y retains its value for some time. Such measurements are not harmless interventions. A system in which such measurements occur shows a sort of memory faculty, in the sense that one can recognize by the state parameter y what value another state parameter x had at an earlier moment, and we shall see that simply because of such a memory the Second Law would be violated, if the measurement could take place without compensation. We shall realize that the Second Law is not threatened as much by this entropy decrease as one would think, as soon as we see that the entropy decrease resulting from the intervention would be compensated completely in any event if the execution of such a measurement were, for instance, always accompanied by production of k log 2 units of entropy. In that case it will be possible to find a more general entropy law, which applies universally to all measurements. Finally we shall consider a very simple (of course, not living) device, that is able to make measurements continually and whose "biological phenomena" we can easily follow. By direct calculation, one finds in fact a continual entropy production of the magnitude required by the above-mentioned more general entropy law derived from the validity of the Second Law.
The first example, which we are going to consider more closely as a typical one, is the following. A standing hollow cylinder, closed at both ends, can be separated into two possibly unequal sections of volumes V1 and V2 respectively by inserting a partition from the side at an arbitrarily fixed height. This partition forms a piston that can be moved up and down in the cylinder. An infinitely large heat reservoir of a given temperature T insures that any gas present in the cylinder undergoes isothermal expansion as the piston moves. This gas shall consist of a single molecule which, as long as the piston is not inserted into the cylinder, tumbles about in the whole cylinder by virtue of its thermal motion.
Imagine, specifically, a man who at a given time inserts the piston into the cylinder and somehow notes whether the molecule is caught in the upper or lower part of the cylinder, that is, in volume V1 or V2. If he should find that the former is the case, then he would move the piston slowly downward until it reaches the bottom of the cylinder. During this slow movement of the piston the molecule stays, of course, above the piston.
However, it is no longer constrained to the upper part of the cylinder but bounces many times against the piston which is already moving in the lower part of the cylinder. In this way the molecule does a certain amount of work on the piston. This is the work that corresponds to the isothermal expansion of an ideal gas - consisting of one single molecule from volume V1 to the volume V1 + V2. After some time, when the pistol has reached the bottom of the container, the molecule has again the full volume V to move about in, and the piston is then removed. The procedure can be repeated as many times as desired. The man moves the piston up or down depending on whether the molecule is trapped in the upper or lower half of the piston. In more detail, this motion may be caused by a weight, that is to be raised, through a mechanism that transmits the force from the piston to the weight, in such a way that the latter is always displaced upwards. In this way the potential energy of the weight certainly increases constantly. (The transmission of force to the weight is best arranged so that the force exerted by the weight on the piston at any position of the latter equals the average pressure of the gas.) It is clear that in this manner energy is constantly gained at the expense of heat, insofar as the biological phenomena of the intervening man are ignored in the calculation.
In order to understand the essence of the man's effect on the system, one best imagines that the movement of the piston is performed mechanically and that the man's activity consists only in determining the altitude of the molecule and in pushing a lever (which steers the piston) to the right or left, depending on whether the molecule's height requires a down- or upward movement. This means that the intervention of the human being consists only in the coupling of two position co-ordinates, namely a co-ordinate x, which determines the altitude of the molecule, with another co-ordinate y, which determines the position of the lever and therefore also whether an upward or downward motion is imparted to the piston. It is best to imagine the mass of the piston as large and its speed sufficiently great, so that the thermal agitation of the piston at the temperature in question can be neglected.
In the typical example presented here, we wish to distinguish two periods, namely:
1. The period of measurement when the piston has just been inserted in the middle of the cylinder and the molecule is trapped either in the upper or lower part; so that if we choose the origin of co-ordinates appropriately, the x-co-ordinate of the molecule is restricted to either the interval x > 0 or x < 0;
2. The period of utilization of the measurement, "the period of decrease of entropy," during which the piston is moving up or down. During this period the x-co-ordinate of the molecule is certainly not restricted to the original interval x > 0 or x < 0. Rather, if the molecule was in the upper half of the cylinder during the period of measurement, i.e., when x > 0, the molecule must bounce on the downward-moving piston in the lower part of the cylinder, if it is to transmit energy to the piston; that is, the co-ordinate x has to enter the interval x < 0. The lever, on the contrary, retains during the whole period its position toward the right, corresponding to downward motion. If the position of the lever toward the right is designated by y = 1 (and correspondingly the position toward the left by y = —1) we see that during the period of measurement, the position x > 0 corresponds to y = 1; but afterwards y = 1 stays on, even though x passes into the other interval x < 0. We see that in the utilization of the measurement the coupling of the two parameters x and y disappears.
We shall say, quite generally, that a parameter y "measures" a parameter x (which varies according to a probability law), if the value of y is directed by the value of parameter x at a given moment. A measurement procedure underlies the entropy decrease effected by the intervention of intelligent beings.
One may reasonably assume that a measurement procedure is fundamentally associated with a certain definite average entropy production, and that this restores concordance with the Second Law. The amount of entropy generated by the measurement may, of course, always be greater than this fundamental amount, hut not smaller. To put it precisely: we have to distinguish here between two entropy values. One of them, S1 , is produced when during the measurement y assumes the value 1, and the other, S2, when y assumes the value —1. We cannot expect to get general information about S1 or S2 separately, but we shall see that if the amount of entropy produced by the "measurement" is to compensate the entropy decrease affected by utilization, the relation must always hold good.
e-S1/k + e-S2/k ≤ 1 (1)
One sees from this formula that one can make one of the values, for instance S1, as small as one wishes, hut then the other value S2 becomes correspondingly greater. Furthermore, one can notice that the magnitude of the interval under consideration is of no consequence. One can also easily understand that it cannot be otherwise.
Conversely, as long as the entropies S1 and
S2, produced by the measurements, satisfy the inequality (1), we can he sure that the expected decrease of entropy caused by the later utilization of the measurement will be fully compensated.
Before we proceed with the proof of inequality (1), let us see in the light of the above mechanical example, how all this fits together. For the entropies S1 and S2 produced by the measurements, we make the following Ansatz:
S1 = S2 = k log 2 (2)
This ansatz satisfies inequality (1) and the mean value of the quantity of entropy produced by a measurement is (of course in this special case independent of the frequencies ω1, ω2 of the two events):
S = k log 2 (3)
REFERENCES
Smoluchowski, F. Vorträge über die kinetische Theorie der Materie u. Elektrizitat. Leipzig: 1914.
Szilard, L. Zeitschrift. fur Physik, 1925, 32, 753.
|