Huw Price was born in Oxford, England and was a professor of logic and metaphysics at Edinburgh. But he developed his original philosophical ideas in Australia as professor of philosophy at the University of Sydney. There he directed the Centre for Time and proposed that physicists and philosophers look at the world from the perspective of an "Archimedean point" outside space and time that provides a symmetric view of the past and the future.

Price's ideas are inspired by the "block universe" of Einstein-Minkowski special relativity. A generation before Price was in Sydney, Australian philosopher J. J. C. Smart developed a "tenseless" theory of space and time and maintained that there is but one possible future.

Smart was one of the original architects of the standard argument against free will and Price developed an argument based on the work of John Bell that giving up free will (what Niels Bohr and Werner Heisenberg called the "free choice" of the experimenter) could remove a conflict between special relativity and the measurements of entangled systems in which something appears to be traveling faster than the speed of light.

The free choice of the experimenter was explored by John Conway and Simon Kochen. They claim that if free choice exists, it shows that atoms themselves must have free will, something they call the Free Will Theorem.

In his 1996 book, Time's Arrow and Archimedes' Point, Price proposes an Archimedean point "outside space and time" as a solution to the problem of nonlocality in the Bell experiments in the form of an "advanced action."

John Bell, and more recently, following Bell, Nicholas Gisin and Antoine Suarez claim that something might be coming from "outside space and time" to correlate the results in the spacelike-separated experimental tests of Bell's Theorem.

Rather than a "superdeterministic" common cause coming from "outside space and time" (as proposed by Bell, Gisin, Suarez, and others), Price argues that there might be a cause coming backwards in time from some interaction in the future. Roger Penrose and Stuart Hameroff have also promoted this idea of "backward causation," sending information backward in time in the Libet experiments and in the EPR experiments.

John Cramer's Transactional Interpretation of quantum mechanics and other Time-Symmetric Interpretations like that of Yakir Aharonov and K. B Wharton also search for Archimedean points "outside space and time."

But there is another way to get a time-symmetric point of view that resolves the EPR paradox of "influence" traveling faster than the speed of light. In his chapter on John Bell in Time's Arrow..., Price cites a BBC interview in which Bell suggested that a preferred frame of reference might help to explain nonlocality and entanglement.

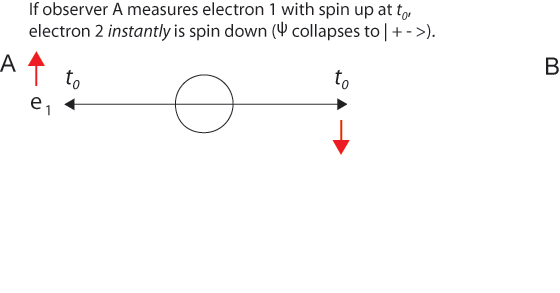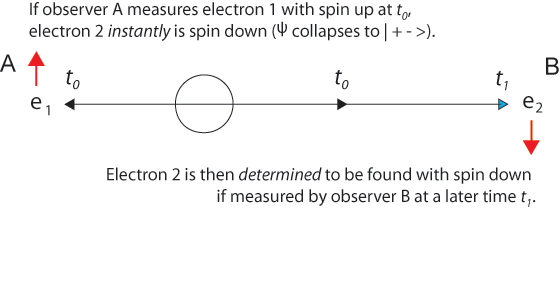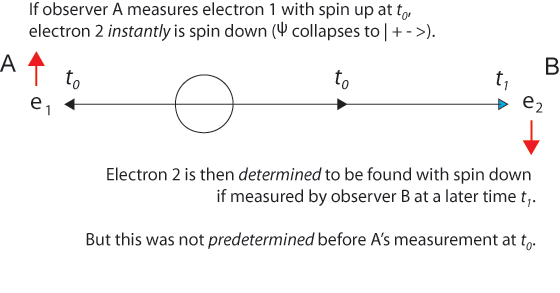
[Davies] Bell's inequality is, as I understand it, rooted in two assumptions: the first is what we might call objective reality - the reality of the external world, independent of our observations; the second is locality, or non-separability, or no faster-than-light signalling. Now, Aspect's experiment appears to indicate that one of these two has to go. Which of the two would you like to hang on to?

[Bell] Well, you see, I don't really know. For me it's not something where I have a solution to sell! For me it's a dilemma. I think it's a deep dilemma, and the resolution of it will not be trivial; it will require a substantial change in the way we look at things. But I would say that the cheapest resolution is something like going back to relativity as it was before Einstein, when people like Lorentz and Poincare thought that there was an aether - a preferred frame of reference - but that our measuring instruments were distorted by motion in such a way that we could not detect motion through the aether. Now, in that way you can imagine that there is a preferred frame of reference, and in this preferred frame of reference things do go faster than light. But then in other frames of reference when they seem to go not only faster than light but backwards in time, that is an optical illusion.

(The Ghost in the Atom, P.C.W. Davies and J. Brown, ch.3, p.48-9, bold italic section cited by Price, Time's Arrow...", p. 231))

The standard explanation of entangled particles usually begins with an observer A, often called Alice, and a distant observer B, known as Bob. Between them is a source of two entangled particles. The two-particle wave function describing the indistinguishable particles cannot be separated into a product of two single-particle wave functions.

The problem of faster-than-light signaling arises when Alice is said to measure particle A and then puzzle over how Bob's (later) measurements of particle B can be perfectly correlated, when there is not enough time for any "influence" to travel from A to B.

Price describes the problem (p.202):

"the results of measurement on one particle enable us to predict the results of corresponding measurements on the other particle. For example, we might predict the position of particle 1 by measuring the position of particle 2, or predict the momentum of particle 2 by measuring the momentum of particle 1.

Like Price's description, Bell's own description of the process shows a mistaken bias toward assuming first one measurement is made, and the other measurement is made later.

If measurement of the component σ₁ • a, where a is some unit vector, yields the value + 1 then, according to quantum mechanics, measurement of σ₂ • a must yield the value — 1 and vice versa... Since we can predict in advance the result of measuring any chosen component of σ₂, by previously measuring the same component of σ₁, it follows that the result of any such measurement must actually be predetermined.

("On the Einstein-Podolsky-Rosen Paradox," J. Bell, 1964)

But note that Price's formulation is nicely symmetric. Measurement 1 can influence measurement 2, and measurement 2 can influence measurement 1. How can this be? Can we see how time asymmetry mistakenly enters the description and is the source of the EPR paradox?

As John Bell knew very well, there are frames of reference moving with respect to the laboratory frame of the two observers in which the time order of the events can be reversed. In some moving frames Alice measures first, but in others Bob measures first.

If there is a preferred frame of reference (we might call it a special frame to avoid confusion with relativity?), surely it is the one in which the origin of the two entangled particles is at rest. Assuming that Alice and Bob are also at rest in this preferred frame and equidistant from the origin, we arrive at the simple picture in which any measurement that causes the two-particle wave function to collapse makes both particles appear simultaneously at determinate places (just what is needed to conserve energy, momentum, angular momentum, and spin).

In the two-particle case (instead of just one particle making an appearance), when either particle is measured, we know instantly those properties of the other particle that satisfy the conservation laws, including its location equidistant from, but on the opposite side of, the source, and its other properties such as spin.

Let's look at an animation of the two-particle wave function expanding from the origin and what happens when, say, Alice makes a measurement.

We can also ask what happens if Bob is not at the same distance from the origin as Alice. This introduces a positional asymmetry. But there is still no time asymmetry from the point of view of the two-particle wave function collapse.

When Alice detects the particle (with say spin up), at that instant the other particle also becomes determinate (with spin down) at the same distance on the other side of the origin. It now continues, in that determinate state, to Bob's measuring apparatus.

In his Time's Arrow... book, Price reviews three basic arrows of time, the thermodynamic arrow, the radiation arrow, and the cosmological arrow. He describes Ludwig Boltzmann's statistical derivation of the second law of thermodynamics based on his H-Theorem, which predicts that entropy will increase (symmetrically) in both the future and the past from a given present entropy that is not equilibrium. He likes Boltzmann's speculation that the direction of time may be only subjective.

In the late nineteenth century, as thermodynamics came to be addressed in terms of the symmetric framework of statistical mechanics, the puzzle just described came slowly into view: where does the asymmetry of the second law come from? I shall explain how, as this problem came into view, it produced the first examples of a kind of fallacy which has often characterized attempts to explain temporal asymmetry in physics. This fallacy involves a kind of special pleading, or double standard. It takes an argument which could be used equally well in either temporal direction and applies it selectively, in one direction but not the other. Not surprisingly, this biased procedure leads to asymmetric conclusions. Without a justification for the bias, however, these conclusions tell us nothing about the origins of the real asymmetry we find in the world.

(Time's Arrow and Archimedes' Point, p.6)

The cosmologist Thomas Gold once suggested that the expansion of the universe might eventually turn around and contract back to a state of low entropy like the beginning of the universe. Price explores what he calls "Gold universes." But he finds what he calls a "basic dilemma," a conflict between Gold's view and certain initial conditions for the universe.

Microscopic innocence assumes that when quantum particles approach one another in a collision that there is no information in their paths that biases them to behave in other than the probabilities predicted by quantum mechanics. Ludwig Boltzmann and E.H. Culverwell called this the hypothesis of molecular disorder. In other places, Price calls this the Principle of the Independence of Incoming Influences.

Price looks at the very simple example of a photon interacting with a polarizer. If at some time in the past the photon had been already polarized vertically, then its chances of passing through a horizontal polarizer now are nil and its probability of passing through a vertical polarizer are unity (P = 1, or certainty). (Wolfgang Pauli called it a measurement of the first kind when a system is prepared (by a measurement) in a known state and then measured again to see if it is in the same state.) A polarized photon has what Price might call a dependence on an incoming influence.

Price sees Albert Einstein's 1905 insight that electromagnetic radiation is particle-like to be foundational. And he says it is ironic that a generation later, Einstein's dream of a more realistic and more complete theory (based on a continuous field theory) was viewed as reactionary. Einstein's idea of an objective world existing independently of human observers was rejected by the Copenhagen Interpretation of Bohr and Heisenberg, which made quantum physics dependent on the mind of the observer.

In a recent paper on the arrow of radiation, Price discusses the thermodynamic arrow as the consequence of initial conditions, which could equally well be final conditions. He reviews Ludwig Boltzmann's work

To illustrate Boltzmann’s approach, think of a large collection of gas molecules, isolated in a box with elastic walls. If the motion of the molecules is governed by deterministic laws, a specification of the microstate of the system at any one time uniquely determines its entire trajectory. The key to Boltzmann’s approach is that in the overwhelming majority of possible trajectories, the system spends the overwhelming majority of the time in a high entropy macrostate — among other things, a state in which the gas is dispersed throughout the container.

Importantly, there is no temporal bias in this set of possible trajectories. Each possible trajectory is matched by its time-reversed twin, just as Loschmidt had pointed out, and the Boltzmann measure respects this symmetry. Asymmetry arises only when we apply a low entropy condition at one end. For example, suppose we stipulate that the gas is confined to some small region at the initial time t₀. Restricted to the remaining trajectories, the Boltzmann measure now provides a measure of the likelihood of the various possibilities consistent with this boundary condition. Almost all trajectories in this remaining set will be such that the gas disperses after t₀. The observed behaviour is thus predicted by the time-symmetric measure, once we conditionalise on the low entropy condition at t₀.

On this view, then, there’s no time-asymmetric factor which causes entropy to increase in one direction. This is simply the most likely thing to happen, given the combination of the time-symmetric Boltzmann probabilities and the single low entropy restriction in the past. This ‘boundary condition’ is time asymmetric, so far as we know, but it is the only time-asymmetry in play, according to Boltzmann’s approach...

One more point about the particle case, before we return to radiation. Because Boltzmann’s one-asymmetry approach traces the observed asymmetry of thermodynamics entirely to the low entropy initial condition, it doesn’t provide a statistical argument against the existence of a similar final condition. On the contrary: within the abstract framework of Boltzmann’s approach, the issue as to whether there is such a future low entropy boundary condition is effectively the same as the question whether the time-symmetric Boltzmann measure is reliable towards the future, in the way in which it turns out not to be reliable towards the past – so we certainly can’t appeal to the Boltzmann measure itself to settle the issue!

(Recent Work on the Arrow of Radiation, pp.17-18)

Chapter 1.4 - The Philosophy	Chapter 1.6 - The Scientists
Home	Part Two - Knowledge