|
Topics
Introduction
Problems Freedom Knowledge Mind Life Chance Quantum Entanglement Scandals Philosophers Mortimer Adler Rogers Albritton Alexander of Aphrodisias Samuel Alexander William Alston Anaximander G.E.M.Anscombe Anselm Louise Antony Thomas Aquinas Aristotle David Armstrong Harald Atmanspacher Robert Audi Augustine J.L.Austin A.J.Ayer Alexander Bain Mark Balaguer Jeffrey Barrett William Barrett William Belsham Henri Bergson George Berkeley Isaiah Berlin Richard J. Bernstein Bernard Berofsky Robert Bishop Max Black Susan Blackmore Susanne Bobzien Emil du Bois-Reymond Hilary Bok Laurence BonJour George Boole Émile Boutroux Daniel Boyd F.H.Bradley C.D.Broad Michael Burke Jeremy Butterfield Lawrence Cahoone C.A.Campbell Joseph Keim Campbell Rudolf Carnap Carneades Nancy Cartwright Gregg Caruso Ernst Cassirer David Chalmers Roderick Chisholm Chrysippus Cicero Tom Clark Randolph Clarke Samuel Clarke Anthony Collins August Compte Antonella Corradini Diodorus Cronus Jonathan Dancy Donald Davidson Mario De Caro Democritus William Dembski Brendan Dempsey Daniel Dennett Jacques Derrida René Descartes Richard Double Fred Dretske Curt Ducasse John Earman Laura Waddell Ekstrom Epictetus Epicurus Austin Farrer Herbert Feigl Arthur Fine John Martin Fischer Frederic Fitch Owen Flanagan Luciano Floridi Philippa Foot Alfred Fouilleé Harry Frankfurt Richard L. Franklin Bas van Fraassen Michael Frede Gottlob Frege Peter Geach Edmund Gettier Carl Ginet Alvin Goldman Gorgias Nicholas St. John Green Niels Henrik Gregersen H.Paul Grice Ian Hacking Ishtiyaque Haji Stuart Hampshire W.F.R.Hardie Sam Harris William Hasker R.M.Hare Georg W.F. Hegel Martin Heidegger Heraclitus R.E.Hobart Thomas Hobbes David Hodgson Shadsworth Hodgson Baron d'Holbach Ted Honderich Pamela Huby David Hume Ferenc Huoranszki Frank Jackson William James Lord Kames Robert Kane Immanuel Kant Tomis Kapitan Walter Kaufmann Jaegwon Kim William King Hilary Kornblith Christine Korsgaard Saul Kripke Thomas Kuhn Andrea Lavazza James Ladyman Christoph Lehner Keith Lehrer Gottfried Leibniz Jules Lequyer Leucippus Michael Levin Joseph Levine George Henry Lewes C.I.Lewis David Lewis Peter Lipton C. Lloyd Morgan John Locke Michael Lockwood Arthur O. Lovejoy E. Jonathan Lowe John R. Lucas Lucretius Alasdair MacIntyre Ruth Barcan Marcus Tim Maudlin James Martineau Nicholas Maxwell Storrs McCall Hugh McCann Colin McGinn Michael McKenna Brian McLaughlin John McTaggart Paul E. Meehl Uwe Meixner Alfred Mele Trenton Merricks John Stuart Mill Dickinson Miller G.E.Moore Ernest Nagel Thomas Nagel Otto Neurath Friedrich Nietzsche John Norton P.H.Nowell-Smith Robert Nozick William of Ockham Timothy O'Connor Parmenides David F. Pears Charles Sanders Peirce Derk Pereboom Steven Pinker U.T.Place Plato Karl Popper Porphyry Huw Price H.A.Prichard Protagoras Hilary Putnam Willard van Orman Quine Frank Ramsey Ayn Rand Michael Rea Thomas Reid Charles Renouvier Nicholas Rescher C.W.Rietdijk Richard Rorty Josiah Royce Bertrand Russell Paul Russell Gilbert Ryle Jean-Paul Sartre Kenneth Sayre T.M.Scanlon Moritz Schlick John Duns Scotus Albert Schweitzer Arthur Schopenhauer John Searle Wilfrid Sellars David Shiang Alan Sidelle Ted Sider Henry Sidgwick Walter Sinnott-Armstrong Peter Slezak J.J.C.Smart Saul Smilansky Michael Smith Baruch Spinoza L. Susan Stebbing Isabelle Stengers George F. Stout Galen Strawson Peter Strawson Eleonore Stump Francisco Suárez Richard Taylor Kevin Timpe Mark Twain Peter Unger Peter van Inwagen Manuel Vargas John Venn Kadri Vihvelin Voltaire G.H. von Wright David Foster Wallace R. Jay Wallace W.G.Ward Ted Warfield Roy Weatherford C.F. von Weizsäcker William Whewell Alfred North Whitehead David Widerker David Wiggins Bernard Williams Timothy Williamson Ludwig Wittgenstein Susan Wolf Xenophon Scientists David Albert Philip W. Anderson Michael Arbib Bobby Azarian Walter Baade Bernard Baars Jeffrey Bada Leslie Ballentine Marcello Barbieri Jacob Barandes Julian Barbour Horace Barlow Gregory Bateson Jakob Bekenstein John S. Bell Mara Beller Charles Bennett Ludwig von Bertalanffy Susan Blackmore Margaret Boden David Bohm Niels Bohr Ludwig Boltzmann John Tyler Bonner Emile Borel Max Born Satyendra Nath Bose Walther Bothe Jean Bricmont Hans Briegel Leon Brillouin Daniel Brooks Stephen Brush Henry Thomas Buckle S. H. Burbury Melvin Calvin William Calvin Donald Campbell John O. Campbell Sadi Carnot Sean B. Carroll Anthony Cashmore Eric Chaisson Gregory Chaitin Jean-Pierre Changeux Rudolf Clausius Arthur Holly Compton John Conway Simon Conway-Morris Peter Corning George Cowan Jerry Coyne John Cramer Francis Crick E. P. Culverwell Antonio Damasio Olivier Darrigol Charles Darwin Paul Davies Richard Dawkins Terrence Deacon Lüder Deecke Richard Dedekind Louis de Broglie Stanislas Dehaene Max Delbrück Abraham de Moivre David Depew Bernard d'Espagnat Paul Dirac Theodosius Dobzhansky Hans Driesch John Dupré John Eccles Arthur Stanley Eddington Gerald Edelman Paul Ehrenfest Manfred Eigen Albert Einstein George F. R. Ellis Walter Elsasser Hugh Everett, III Franz Exner Richard Feynman R. A. Fisher David Foster Joseph Fourier George Fox Philipp Frank Steven Frautschi Edward Fredkin Augustin-Jean Fresnel Karl Friston Benjamin Gal-Or Howard Gardner Lila Gatlin Michael Gazzaniga Nicholas Georgescu-Roegen GianCarlo Ghirardi J. Willard Gibbs James J. Gibson Nicolas Gisin Paul Glimcher Thomas Gold A. O. Gomes Brian Goodwin Julian Gough Joshua Greene Dirk ter Haar Jacques Hadamard Mark Hadley Ernst Haeckel Patrick Haggard J. B. S. Haldane Stuart Hameroff Augustin Hamon Sam Harris Ralph Hartley Hyman Hartman Jeff Hawkins John-Dylan Haynes Donald Hebb Martin Heisenberg Werner Heisenberg Hermann von Helmholtz Grete Hermann John Herschel Francis Heylighen Basil Hiley Art Hobson Jesper Hoffmeyer John Holland Don Howard John H. Jackson Ray Jackendoff Roman Jakobson E. T. Jaynes William Stanley Jevons Pascual Jordan Eric Kandel Ruth E. Kastner Stuart Kauffman Martin J. Klein William R. Klemm Christof Koch Simon Kochen Hans Kornhuber Stephen Kosslyn Daniel Koshland Ladislav Kovàč Leopold Kronecker Bernd-Olaf Küppers Rolf Landauer Alfred Landé Pierre-Simon Laplace Karl Lashley David Layzer Joseph LeDoux Gerald Lettvin Michael Levin Gilbert Lewis Benjamin Libet David Lindley Seth Lloyd Werner Loewenstein Hendrik Lorentz Josef Loschmidt Alfred Lotka Ernst Mach Donald MacKay Henry Margenau Lynn Margulis Owen Maroney David Marr Humberto Maturana James Clerk Maxwell John Maynard Smith Ernst Mayr John McCarthy Barbara McClintock Warren McCulloch N. David Mermin George Miller Stanley Miller Ulrich Mohrhoff Jacques Monod Vernon Mountcastle Gerd B. Müller Emmy Noether Denis Noble Donald Norman Travis Norsen Howard T. Odum Alexander Oparin Abraham Pais Howard Pattee Wolfgang Pauli Massimo Pauri Wilder Penfield Roger Penrose Massimo Pigliucci Steven Pinker Colin Pittendrigh Walter Pitts Max Planck Susan Pockett Henri Poincaré Michael Polanyi Daniel Pollen Ilya Prigogine Hans Primas Giulio Prisco Zenon Pylyshyn Henry Quastler Adolphe Quételet Pasco Rakic Nicolas Rashevsky Lord Rayleigh Frederick Reif Jürgen Renn Giacomo Rizzolati A.A. Roback Emil Roduner Juan Roederer Robert Rosen Frank Rosenblatt Jerome Rothstein David Ruelle David Rumelhart Michael Ruse Stanley Salthe Robert Sapolsky Tilman Sauer Ferdinand de Saussure Jürgen Schmidhuber Erwin Schrödinger Aaron Schurger Sebastian Seung Thomas Sebeok Franco Selleri Claude Shannon James A. Shapiro Charles Sherrington Abner Shimony Herbert Simon Dean Keith Simonton Edmund Sinnott B. F. Skinner Lee Smolin Ray Solomonoff Herbert Spencer Roger Sperry John Stachel Kenneth Stanley Henry Stapp Ian Stewart Tom Stonier Antoine Suarez Leonard Susskind Leo Szilard Max Tegmark Teilhard de Chardin Libb Thims William Thomson (Kelvin) Richard Tolman Giulio Tononi Peter Tse Alan Turing Robert Ulanowicz C. S. Unnikrishnan Nico van Kampen Francisco Varela Vlatko Vedral Vladimir Vernadsky Clément Vidal Mikhail Volkenstein Heinz von Foerster Richard von Mises John von Neumann Jakob von Uexküll C. H. Waddington Sara Imari Walker James D. Watson John B. Watson Daniel Wegner Steven Weinberg August Weismann Paul A. Weiss Herman Weyl John Wheeler Jeffrey Wicken Wilhelm Wien Norbert Wiener Eugene Wigner E. O. Wiley E. O. Wilson Günther Witzany Carl Woese Stephen Wolfram H. Dieter Zeh Semir Zeki Ernst Zermelo Wojciech Zurek Konrad Zuse Fritz Zwicky Presentations ABCD Harvard (ppt) Biosemiotics Free Will Mental Causation James Symposium CCS25 Talk Evo Devo September 12 Evo Devo October 2 Evo Devo Goodness Evo Devo Davies Nov12 |
Nonseparability
The idea of something measured in one place "influencing" measurements far away challenged what Einstein thought of as "local reality." It came to be known as "nonlocality," but it always contained something else called "nonseparability." Einstein called it "spukhaft Fernwirkung" or "spooky action at a distance." Erwin Schrödinger called two particles "verschrankt" or "entangled" when their quantum properties had become correlated by an interaction. Entangled particles cannot be separated without an external interaction.
The question for Einstein and Schrödinger was how long the particles could retain their correlation as they traveled a great distance apart. Once de-correlated or "decohered," their two-particle wave function can be described as the product of two single-particle wave functions and there will no longer be any quantum interference (or the appearance of communications or interactions between them) between them. But entangled particles, it turns out, cannot be decohered without an external interaction of some kind (like a measurement).
Einstein had objected to nonlocal phenomena as early as the Solvay Conference of 1927, when he criticized the collapse of the wave function as involving "instantaneous-action-at-a-distance" (his spukhafte Fernwerkung or "spooky action at a distance") that prevents the spherical outgoing wave from acting at more than one place on the screen. He probably had seen this nonlocality as early as his light-quantum hypothesis paper of 1905.
Single-particle nonlocality can be defined in terms of the volume in phase space where the wave function has non-zero values. There are possibilities of finding the particle anywhere in this volume (with a calculable probability for each possibility).
A particle appears when one of those possibilities becomes actual and the particle is localized. This can be the result of an observer making a measurement or a random environmental interaction. The "collapse" of the wave function is then simply the instantaneous disappearance, the going to zero, of all the non-actualized possibilities when the nonlocal wave becomes a localized particle.
Einstein insisted that when two particles have separated enough there would come a distance where interactions between them are no longer possible. He called this his Trennungsprinzip or separability principle.
We can now understand the "nonseparability" of two entangled particles in terms of this nonlocality. Two entangled particles are described by a two-particle wave function that can not be factored into the product of two single-particle wave functions. The entangled particles share the same volume of nonlocality, i.e., where the two-particle wave function has non-zero values.
This means that either particle has the same possibility (with calculable probability) of appearing at any particular location. Just as with the single-particle nonlocality, we cannot say where the particles "are." Either one may be anywhere inside the nonlocality volume up to the moment of "collapse" of the two-particle wave function.
So far this is what Richard Feynman called the "only mystery" in quantum mechanics. He mistakenly advised you not to try to understand it or visualize it, but information physics will help you to do both, for single particles, such as the two-slit experiment, and for the two-particle Einstein-Podolsky-Rosen thought experiment.
When the entangled particles experience a random environmental interaction (described as "decoherence"), or an experimental measurement by an observer, the two-particle wave function "collapses." All the possibilities/probabilities that are not actualized go to zero, just as with the single particle wave function. But now, two particles appear, simultaneously in a special frame in which their center of mass is not moving. In other frames, one may appear to appear before the other.
Just as with the single particle, the localization of the two particles can be anywhere there was a possibility. But now fundamental conservation principles constrain their local appearances.The two particles appear simultaneously, usually in a spacelike separation, now disentangled, and symmetrically located about the point of the interaction which entangled them.

Einstein's Introduction of Asymmetry
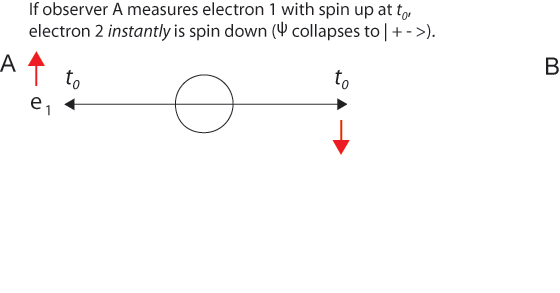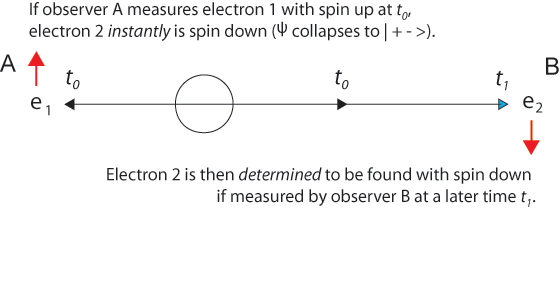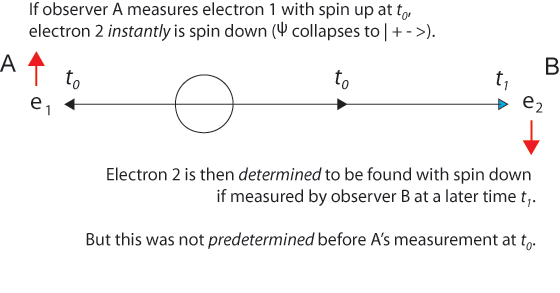
Almost every presentation of the EPR paradox begins with something like "Alice observes one particle..." and concludes with the question "How does the second particle get the information needed so that Bob's later measurements correlate perfectly with Alice?"
There is a fundamental asymmetry in this framing of the EPR experiment. It is a surprise that Einstein, who was so good at seeing deep symmetries, did not consider how to remove the asymmetry.
Consider this reframing: Alice's measurement collapses the two-particle wave function. The two indistinguishable particles simultaneously appear at locations in a space-like separation. The frame of reference in which the source of the two entangled particles and the two experimenters are at rest is a special frame in the following sense.
As Einstein knew very well, there are frames of reference moving with respect to the laboratory frame of the two observers in which the time order of the events can be reversed. In some moving frames Alice measures first, but in others Bob measures first.
If there is a special frame of reference (not a preferred frame in the relativistic sense), surely it is the one in which the origin of the two entangled particles is at rest. Assuming that Alice and Bob are also at rest in this special frame and equidistant from the origin, we arrive at the simple picture in which any measurement that causes the two-particle wave function to collapse makes both particles appear simultaneously at determinate places with fully correlated properties (just those that are needed to conserve energy, momentum, angular momentum, and spin).

|