For over sixty years, since I first read Arthur Stanley Eddington's The Nature of the Physical World, I have been struggling, as the "information philosopher," to understand and to find simpler ways to explain the concept of entropy.

Even more challenging has been to find the best way to teach the mathematical and philosophical connections between entropy and information. A great deal of the literature complains that these concepts are too difficult to understand and may have nothing to do with one another.

Finally, there is the important concept of probability, with its implication of possibilities, one or more of which may become an actuality.

Determinist philosophers (perhaps a majority) and scientists (a strong minority) say that we use probability and statistics only because our finite minds are incapable of understanding reality. Their idea of the universe is that it contains infinite information which only an infinite mind can comprehend. Our observable universe contains a very large but finite amount of information. Entropy is a measure of that lost energy.

A very strong connection between entropy and probability is obvious because Ludwig Boltzmann's formula for entropy S = logW, where W stands for Wahrscheinlichkeit, the German for probability. We believe that Rudolf Clausius, who first defined and named entropy, gave it the symbol S in honor of Sadi Carnot, whose study of heat engine efficiency showed that some fraction of available energy is always wasted or dissipated, only a part can be converted to mechanical work.

is mathematically identical to Claude Shannon's expression for information I, but with a minus sign and different dimensions.

Boltzmann entropy: S = k ∑ p_i ln p_i.        Shannon information: I = - ∑ p_i ln p_i.

Boltzmann entropy and Shannon entropy have different dimensions (S = joules/°K,
I = dimensionless "bits"), but they share the "mathematical isomorphism" of a logarithm of probabilities, which is the basis of both Boltzmann's and Gibbs' statistical mechanics..

The first entropy is material, the latter mathematical - indeed purely immaterial information.

But they have deeply important connections which information philosophy must sort out and explain.

First, both Boltzmann and Shannon expressions contain probabilities and statistics. Many philosophers and scientists deny any ontological indeterminism, such as the chance in quantum mechanics discovered by Albert Einstein in 1916. They may accept an epistemological uncertainty, as proposed by Werner Heisenberg in 1927.

Today many thinkers propose chaos and complexity theories (both theories are completely deterministic) as adequate explanations, while they deny ontological chance. Ontological chance is the basis for creating any information structure. It explains the variation in species needed for Darwinian evolution. It underlies human freedom and the creation of new ideas.

In statistical mechanics, the summation ∑ is over all the possible distributions of gas particles in a container. If the number of distributions is W , and the probability of all distributions is the same, the p_i are all equal to 1/W and entropy is maximal: S = k ∑ 1/W ln 1/W, so S = k ln W.

In the communication of information, W is the number of possible messages. If the probability of all messages is the same, p_i are identical, I = - lnW. If there are N possible messages, then N bits of information are communicated by receiving one of them.

On the other hand, if there is only one possible message, its probability is unity, and the information content is 1 ln 0 = zero.

If there is only one possible message, no new information is communicated. This is the case in a deterministic universe, where past events completely cause present events. The information in a deterministic universe is a constant of nature. Religions that include an omniscient god often believe all that information is in God's mind.

Note that if there are no alternative possibilities in messages, Shannon (following his Bell Labs colleague Ralph Hartley) says there can be no new information. We conclude that the creation of new information structures in the universe is only possible because the universe is in fact indeterministic and our futures are open and free.

Thermodynamic entropy involves matter and energy, Shannon entropy is entirely mathematical, on one level purely immaterial information, though it cannot exist without "negative" thermodynamic entropy.

It is true that information is neither matter nor energy, which are conserved constants of nature (the first law of thermodynamics). But information needs matter to be embodied in an "information structure." And it needs ("free") energy to be communicated over Shannon's information channels.

Boltzmann entropy is intrinsically related to "negative entropy." Without pockets of negative entropy in the universe (and out-of-equilibrium free-energy flows), there would no "information structures" anywhere.

Pockets of negative entropy are involved in the creation of everything interesting in the universe. It is a cosmic creation process without a creator.

There is a mistaken idea in statistical physics that any particular distribution or arrangement of material particles has exactly the same information content as any other distribution. This is an anachronism from nineteenth-century deterministic statistical physics.

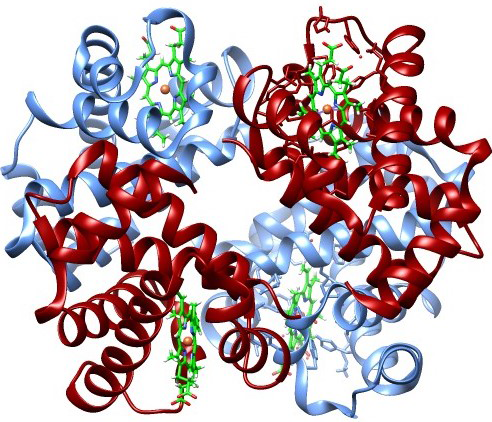Hemoglobin	Diffusing	Completely Mixed Gas

If we measure the positions in phase space of all the atoms in a hemoglobin protein, we get a certain number of bits of data (the x, y, z, v_x, v_y, v_z values). If the chemical bonds are all broken allowing atoms to diffuse, or the atoms are completely randomized into an equilibrium gas with maximum entropy, we get different values, but the same amount of data. Does this mean that any particular distribution has exactly the same information?

This led many statistical physicists to claim that information in a gas is the same wherever the particles are, Macroscopic information is not lost, it just becomes microscopic information that can be completely recovered if the motions of every particle could be reversed. Reversibility allows all the gas particles to go back inside the bottle.

But the information in the hemoglobin is much higher and the disorder (entropy) near zero. A human being is not just a "bag of chemicals," despite plant biologist Anthony Cashmore. Each atom in hemoglobin is not merely in some volume limited by the uncertainty principle ℏ³, it is in a specific quantum cooperative relationship with its neighbors that support its biological function. These precise positional relationships make a passive linear protein into a properly folded active enzyme. Breaking all these quantum chemical bonds destroys life.

Where an information structure is present, the entropy is low and Gibbs free energy is high.

When gas particles can go anywhere in a container, the number of possible distributions is enormous and entropy is maximal. When atoms are bound to others in the hemoglobin structure, the number of possible distributions is essentially 1, and the logarithm of 1 is 0!

Even more important, the parts of every living thing are communicating information - signaling - to other parts, near and far, as well as to other living things. Information communication allows each living thing to maintain itself in a state of homeostasis, balancing all matter and energy entering and leaving, maintaining all vital functions. Statistical physics and chemical thermodynamics know nothing of this biological information.