|
Topics
Introduction
Problems Freedom Knowledge Mind Life Chance Quantum Entanglement Scandals Philosophers Mortimer Adler Rogers Albritton Alexander of Aphrodisias Samuel Alexander William Alston Anaximander G.E.M.Anscombe Anselm Louise Antony Thomas Aquinas Aristotle David Armstrong Harald Atmanspacher Robert Audi Augustine J.L.Austin A.J.Ayer Alexander Bain Mark Balaguer Jeffrey Barrett William Barrett William Belsham Henri Bergson George Berkeley Isaiah Berlin Richard J. Bernstein Bernard Berofsky Robert Bishop Max Black Susan Blackmore Susanne Bobzien Emil du Bois-Reymond Hilary Bok Laurence BonJour George Boole Émile Boutroux Daniel Boyd F.H.Bradley C.D.Broad Michael Burke Jeremy Butterfield Lawrence Cahoone C.A.Campbell Joseph Keim Campbell Rudolf Carnap Carneades Nancy Cartwright Gregg Caruso Ernst Cassirer David Chalmers Roderick Chisholm Chrysippus Cicero Tom Clark Randolph Clarke Samuel Clarke Anthony Collins August Compte Antonella Corradini Diodorus Cronus Jonathan Dancy Donald Davidson Mario De Caro Democritus William Dembski Brendan Dempsey Daniel Dennett Jacques Derrida René Descartes Richard Double Fred Dretske Curt Ducasse John Earman Laura Waddell Ekstrom Epictetus Epicurus Austin Farrer Herbert Feigl Arthur Fine John Martin Fischer Frederic Fitch Owen Flanagan Luciano Floridi Philippa Foot Alfred Fouilleé Harry Frankfurt Richard L. Franklin Bas van Fraassen Michael Frede Gottlob Frege Peter Geach Edmund Gettier Carl Ginet Alvin Goldman Gorgias Nicholas St. John Green Niels Henrik Gregersen H.Paul Grice Ian Hacking Ishtiyaque Haji Stuart Hampshire W.F.R.Hardie Sam Harris William Hasker R.M.Hare Georg W.F. Hegel Martin Heidegger Heraclitus R.E.Hobart Thomas Hobbes David Hodgson Shadsworth Hodgson Baron d'Holbach Ted Honderich Pamela Huby David Hume Ferenc Huoranszki Frank Jackson William James Lord Kames Robert Kane Immanuel Kant Tomis Kapitan Walter Kaufmann Jaegwon Kim William King Hilary Kornblith Christine Korsgaard Saul Kripke Thomas Kuhn Andrea Lavazza James Ladyman Christoph Lehner Keith Lehrer Gottfried Leibniz Jules Lequyer Leucippus Michael Levin Joseph Levine George Henry Lewes C.I.Lewis David Lewis Peter Lipton C. Lloyd Morgan John Locke Michael Lockwood Arthur O. Lovejoy E. Jonathan Lowe John R. Lucas Lucretius Alasdair MacIntyre Ruth Barcan Marcus Tim Maudlin James Martineau Nicholas Maxwell Storrs McCall Hugh McCann Colin McGinn Michael McKenna Brian McLaughlin John McTaggart Paul E. Meehl Uwe Meixner Alfred Mele Trenton Merricks John Stuart Mill Dickinson Miller G.E.Moore Ernest Nagel Thomas Nagel Otto Neurath Friedrich Nietzsche John Norton P.H.Nowell-Smith Robert Nozick William of Ockham Timothy O'Connor Parmenides David F. Pears Charles Sanders Peirce Derk Pereboom Steven Pinker U.T.Place Plato Karl Popper Porphyry Huw Price H.A.Prichard Protagoras Hilary Putnam Willard van Orman Quine Frank Ramsey Ayn Rand Michael Rea Thomas Reid Charles Renouvier Nicholas Rescher C.W.Rietdijk Richard Rorty Josiah Royce Bertrand Russell Paul Russell Gilbert Ryle Jean-Paul Sartre Kenneth Sayre T.M.Scanlon Moritz Schlick John Duns Scotus Albert Schweitzer Arthur Schopenhauer John Searle Wilfrid Sellars David Shiang Alan Sidelle Ted Sider Henry Sidgwick Walter Sinnott-Armstrong Peter Slezak J.J.C.Smart Saul Smilansky Michael Smith Baruch Spinoza L. Susan Stebbing Isabelle Stengers George F. Stout Galen Strawson Peter Strawson Eleonore Stump Francisco Suárez Richard Taylor Kevin Timpe Mark Twain Peter Unger Peter van Inwagen Manuel Vargas John Venn Kadri Vihvelin Voltaire G.H. von Wright David Foster Wallace R. Jay Wallace W.G.Ward Ted Warfield Roy Weatherford C.F. von Weizsäcker William Whewell Alfred North Whitehead David Widerker David Wiggins Bernard Williams Timothy Williamson Ludwig Wittgenstein Susan Wolf Xenophon Scientists David Albert Philip W. Anderson Michael Arbib Bobby Azarian Walter Baade Bernard Baars Jeffrey Bada Leslie Ballentine Marcello Barbieri Jacob Barandes Julian Barbour Horace Barlow Gregory Bateson Jakob Bekenstein John S. Bell Mara Beller Charles Bennett Ludwig von Bertalanffy Susan Blackmore Margaret Boden David Bohm Niels Bohr Ludwig Boltzmann John Tyler Bonner Emile Borel Max Born Satyendra Nath Bose Walther Bothe Jean Bricmont Hans Briegel Leon Brillouin Daniel Brooks Stephen Brush Henry Thomas Buckle S. H. Burbury Melvin Calvin William Calvin Donald Campbell John O. Campbell Sadi Carnot Sean B. Carroll Anthony Cashmore Eric Chaisson Gregory Chaitin Jean-Pierre Changeux Rudolf Clausius Arthur Holly Compton John Conway Simon Conway-Morris Peter Corning George Cowan Jerry Coyne John Cramer Francis Crick E. P. Culverwell Antonio Damasio Olivier Darrigol Charles Darwin Paul Davies Richard Dawkins Terrence Deacon Lüder Deecke Richard Dedekind Louis de Broglie Stanislas Dehaene Max Delbrück Abraham de Moivre David Depew Bernard d'Espagnat Paul Dirac Theodosius Dobzhansky Hans Driesch John Dupré John Eccles Arthur Stanley Eddington Gerald Edelman Paul Ehrenfest Manfred Eigen Albert Einstein George F. R. Ellis Walter Elsasser Hugh Everett, III Franz Exner Richard Feynman R. A. Fisher David Foster Joseph Fourier George Fox Philipp Frank Steven Frautschi Edward Fredkin Augustin-Jean Fresnel Karl Friston Benjamin Gal-Or Howard Gardner Lila Gatlin Michael Gazzaniga Nicholas Georgescu-Roegen GianCarlo Ghirardi J. Willard Gibbs James J. Gibson Nicolas Gisin Paul Glimcher Thomas Gold A. O. Gomes Brian Goodwin Julian Gough Joshua Greene Dirk ter Haar Jacques Hadamard Mark Hadley Ernst Haeckel Patrick Haggard J. B. S. Haldane Stuart Hameroff Augustin Hamon Sam Harris Ralph Hartley Hyman Hartman Jeff Hawkins John-Dylan Haynes Donald Hebb Martin Heisenberg Werner Heisenberg Hermann von Helmholtz Grete Hermann John Herschel Francis Heylighen Basil Hiley Art Hobson Jesper Hoffmeyer John Holland Don Howard John H. Jackson Ray Jackendoff Roman Jakobson E. T. Jaynes William Stanley Jevons Pascual Jordan Eric Kandel Ruth E. Kastner Stuart Kauffman Martin J. Klein William R. Klemm Christof Koch Simon Kochen Hans Kornhuber Stephen Kosslyn Daniel Koshland Ladislav Kovàč Leopold Kronecker Bernd-Olaf Küppers Rolf Landauer Alfred Landé Pierre-Simon Laplace Karl Lashley David Layzer Joseph LeDoux Gerald Lettvin Michael Levin Gilbert Lewis Benjamin Libet David Lindley Seth Lloyd Werner Loewenstein Hendrik Lorentz Josef Loschmidt Alfred Lotka Ernst Mach Donald MacKay Henry Margenau Lynn Margulis Owen Maroney David Marr Humberto Maturana James Clerk Maxwell John Maynard Smith Ernst Mayr John McCarthy Barbara McClintock Warren McCulloch N. David Mermin George Miller Stanley Miller Ulrich Mohrhoff Jacques Monod Vernon Mountcastle Gerd B. Müller Emmy Noether Denis Noble Donald Norman Travis Norsen Howard T. Odum Alexander Oparin Abraham Pais Howard Pattee Wolfgang Pauli Massimo Pauri Wilder Penfield Roger Penrose Massimo Pigliucci Steven Pinker Colin Pittendrigh Walter Pitts Max Planck Susan Pockett Henri Poincaré Michael Polanyi Daniel Pollen Ilya Prigogine Hans Primas Giulio Prisco Zenon Pylyshyn Henry Quastler Adolphe Quételet Pasco Rakic Nicolas Rashevsky Lord Rayleigh Frederick Reif Jürgen Renn Giacomo Rizzolati A.A. Roback Emil Roduner Juan Roederer Robert Rosen Frank Rosenblatt Jerome Rothstein David Ruelle David Rumelhart Michael Ruse Stanley Salthe Robert Sapolsky Tilman Sauer Ferdinand de Saussure Jürgen Schmidhuber Erwin Schrödinger Aaron Schurger Sebastian Seung Thomas Sebeok Franco Selleri Claude Shannon James A. Shapiro Charles Sherrington Abner Shimony Herbert Simon Dean Keith Simonton Edmund Sinnott B. F. Skinner Lee Smolin Ray Solomonoff Herbert Spencer Roger Sperry John Stachel Kenneth Stanley Henry Stapp Ian Stewart Tom Stonier Antoine Suarez Leonard Susskind Leo Szilard Max Tegmark Teilhard de Chardin Libb Thims William Thomson (Kelvin) Richard Tolman Giulio Tononi Peter Tse Alan Turing Robert Ulanowicz C. S. Unnikrishnan Nico van Kampen Francisco Varela Vlatko Vedral Vladimir Vernadsky Clément Vidal Mikhail Volkenstein Heinz von Foerster Richard von Mises John von Neumann Jakob von Uexküll C. H. Waddington Sara Imari Walker James D. Watson John B. Watson Daniel Wegner Steven Weinberg August Weismann Paul A. Weiss Herman Weyl John Wheeler Jeffrey Wicken Wilhelm Wien Norbert Wiener Eugene Wigner E. O. Wiley E. O. Wilson Günther Witzany Carl Woese Stephen Wolfram H. Dieter Zeh Semir Zeki Ernst Zermelo Wojciech Zurek Konrad Zuse Fritz Zwicky Presentations ABCD Harvard (ppt) Biosemiotics Free Will Mental Causation James Symposium CCS25 Talk Evo Devo September 12 Evo Devo October 2 Evo Devo Goodness Evo Devo Davies Nov12 |
Scientists
Michael Arbib John S. Bell Bernard Baars Charles Bennett Ludwig Bertalanffy Margaret Boden David Bohm Neils Bohr Ludwig Boltzmann Emile Borel Max Born Leon Brillouin Stephen Brush Henry Thomas Buckle Donald Campbell Anthony Cashmore Eric Chaisson Jean-Pierre Changeux Arthur Holly Compton John Conway E. H. Culverwell Charles Darwin Abraham de Moivre Paul Dirac John Eccles Arthur Stanley Eddington Paul Ehrenfest Albert Einstein Richard Feynman Joseph Fourier Michael Gazzaniga GianCarlo Ghirardi Nicolas Gisin A.O.Gomes Joshua Greene Jacques Hadamard Patrick Haggard Sam Harris Martin Heisenberg Werner Heisenberg William Stanley Jevons Pascual Jordan Simon Kochen Stephen Kosslyn Rolf Landauer Alfred Landé Pierre-Simon Laplace David Layzer Benjamin Libet Hendrik Lorentz Josef Loschmidt Ernst Mach Henry Margenau James Clerk Maxwell Ernst Mayr Jacques Monod Roger Penrose Steven Pinker Max Planck Henri Poincaré Adolphe Quételet Jerome Rothstein David Ruelle Erwin Schrödinger Aaron Schurger Claude Shannon Herbert Simon Dean Keith Simonton B. F. Skinner Roger Sperry Henry Stapp Antoine Suarez Leo Szilard William Thomson (Kelvin) Peter Tse John von Neumann Daniel Wegner Paul A. Weiss Steven Weinberg Norbert Wiener Eugene Wigner E. O. Wilson H. Dieter Zeh Ernst Zermelo GianCarlo Ghirardi
GianCarlo Ghirardi is the intellectual leader of a group of physicists who want to modify the linear Schrödinger equation, adding nonlinear stochastic terms to cause the "collapse" of the wave function during a quantum measurement.
Ghirardi and his colleagues were motivated by the mysteries of nonlocality and entanglement that appear in Einstein-Podolsky-Rosen experiments, and especially by the enthusiastic support of John Bell for their work.
Bell's Theorem and Inequalities pointed the way to the many physical experiments that have confirmed the standard model of quantum mechanics, but Bell and others were never satisfied that standard quantum mechanics could "explain" what is "really" going on in the microscopic world (despite the extraordinary accuracy of the theory).
The most famous proposal for a solution to these mysteries was Albert Einstein's original criticism that quantum mechanics was "incomplete" and that additional information was needed to restore his intuition of "local reality." David Bohm pursued the search for "hidden variables" that could restore locality and determinism to physics, but the many experimental tests that followed Bell's suggestions have generally ruled out any such local hidden variables.
Ghirardi's work is focused more on an explanation for the sudden "collapse" of the wave function. Bell had criticized the work of John von Neumann, who could not locate the boundary between the quantum system and the classical measuring apparatus. Werner Heisenberg called this a "cut" or "Schnitt" between quantum and classical worlds. Von Neumann said the cut could be located anywhere from the atomic system up to the mind of the conscious observer, injecting an element of subjectivity into the understanding. John Bell called this movable boundary a "shifty split," and illustrated it with a sketch (below).
Ghirardi (with his principal colleagues, Alberto Rimini and Tullio Weber) looks to explain the collapse that accompanies measurement as a consequence of additional random terms which they add to the Schrödinger equation.
The GRW scheme represents a proposal aimed to overcome the difficulties of quantum mechanics discussed by John Bell in his article "Against Measurement." The GRW model is based on the acceptance of the fact that the Schrödinger dynamics, governing the evolution of the wavefunction, has to be modified by the inclusion of stochastic and nonlinear effects. Obviously these modifications must leave practically unaltered all standard quantum predictions about microsystems. To be more specific, the GRW theory admits that the wavefunction, besides evolving through the standard Hamiltonian dynamics, is subjected, at random times, to spontaneous processes corresponding to localisations in space of the microconstituents of any physical system. The mean frequency of the localisations is extremely small, and the localisation width is large on an atomic scale. As a consequence no prediction of standard quantum formalism for microsystems is changed in any appreciable way. The merit of the model is in the fact that the localisation mechanism is such that its frequency increases as the number of constituents of a composite system increases. In the case of a macroscopic object (containing an Avogadro number of constituents) linear superpositions of states describing pointers `pointing simultaneously in different directions' are dynamically suppressed in extremely short times. As stated by John Bell, in GRW Schrödinger's cat is not both dead and alive for more than a split second'.John Bell attacked Max Born's statistical interpretation quantum mechanics and praised GRW in his 1989 "Against Measurement" article: In the beginning, Schrödinger tried to interpret his wavefunction as giving somehow the density of the stuff of which the world is made. He tried to think of an electron as represented by a wavepacket — a wave-function appreciably different from zero only over a small region in space. The extension of that region he thought of as the actual size of the electron — his electron was a bit fuzzy. At first he thought that small wavepackets, evolving according to the Schrödinger equation, would remain small. But that was wrong. Wavepackets diffuse, and with the passage of time become indefinitely extended, according to the Schrödinger equation. But however far the wavefunction has extended, the reaction of a detector to an electron remains spotty. So Schrödinger's 'realistic' interpretation of his wavefunction did not survive. Then came the Born interpretation. The wavefunction gives not the density of stuff, but gives rather (on squaring its modulus) the density of probability. Probability of what exactly? Not of the electron being there, but of the electron being found there, if its position is 'measured*. Why this aversion to 'being' and insistence on 'finding'? The founding fathers were unable to form a clear picture of things on the remote atomic scale. They became very aware of the intervening apparatus, and of the need for a 'classical' base from which to intervene on the quantum system. And so the shifty split. The kinematics of the world, in this orthodox picture, is given a wavefunction (maybe more than one?) for the quantum part, and classical variables — variables which have values — for the classical part: (Ψ(t, q, ...), X(t),...). The Xs are somehow macroscopic. This is not spelled out very explicitly. The dynamics is not very precisely formulated either. It includes a Schrödinger equation for the quantum part, and some sort of classical mechanics for the classical part, and 'collapse' recipes for their interaction. It seems to me that the only hope of precision with the dual (Ψ, x) kinematics is to omit completely the shifty split, and let both Ψ and x refer to the world as a whole. Then the xs must not be confined to some vague macroscopic scale, but must extend to all scales. In the picture of de Broglie and Bohm, every particle is attributed a position x(t). Then instrument pointers — assemblies of particles have positions, and experiments have results. The dynamics is given by the world Schrödinger equation plus precise 'guiding' equations prescribing how the x(t)s move under the influence of Ψ. Particles are not attributed angular momenta, energies, etc., but only positions as functions of time. Peculiar 'measurement' results for angular momenta, energies, and so on, emerge as pointer positions in appropriate experimental setups. Considerations of KG [Kurt Gottfried] and vK [Norman van Kampen] type, on the absence (FAPP) [For All Practical Purposes] of macroscopic interference, take their place here, and an important one, in showing how usually we do not have (FAPP) to pay attention to the whole world, but only to some subsystem and can simplify the wave-function... FAPP. The Born-type kinematics (Ψ, X) has a duality that the original 'density of stuff' picture of Schrödinger did not. The position of the particle there was just a feature of the wavepacket, not something in addition. The Landau—Lifshitz approach can be seen as maintaining this simple non-dual kinematics, but with the wavefunction compact on a macroscopic rather than microscopic scale. We know, they seem to say, that macroscopic pointers have definite positions. And we think there is nothing but the wavefunction. So the wavefunction must be narrow as regards macroscopic variables. The Schrödinger equation does not preserve such narrowness (as Schrödinger himself dramatised with his cat). So there must be some kind of 'collapse' going on in addition, to enforce macroscopic narrowness. In the same way, if we had modified Schrödinger's evolution somehow we might have prevented the spreading of his wavepacket electrons. But actually the idea that an electron in a ground-state hydrogen atom is as big as the atom (which is then perfectly spherical) is perfectly tolerable — and maybe even attractive. The idea that a macroscopic pointer can point simultaneously in different directions, or that a cat can have several of its nine lives at the same time, is harder to swallow. And if we have no extra variables X to express macroscopic definiteness, the wavefunction itself must be narrow in macroscopic directions in the configuration space. This the Landau—Lifshitz collapse brings about. It does so in a rather vague way, at rather vaguely specified times. In the Ghirardi—Rimini—Weber scheme (see the contributions of Ghirardi, Rimini, Weber, Pearle, Gisin and Diosi presented at 62 Years of Uncertainty, Erice, 5-14 August 1989) this vagueness is replaced by mathematical precision. The Schrödinger wavefunction even for a single particle, is supposed to be unstable, with a prescribed mean life per particle, against spontaneous collapse of a prescribed form. The lifetime and collapsed extension are such that departures of the Schrödinger equation show up very rarely and very weakly in few-particle systems. But in macroscopic systems, as a consequence of the prescribed equations, pointers very rapidly point, and cats are very quickly killed or spared. The orthodox approaches, whether the authors think they have made derivations or assumptions, are just fine FAPP — when used with the good taste and discretion picked up from exposure to good examples. At least two roads are open from there towards a precise theory, it seems to me. Both eliminate the shifty split. The de Broglie—Bohm-type theories retain, exactly, the linear wave equation, and so necessarily add complementary variables to express the non-waviness of the world on the macroscopic scale. The GRW-type theories have nothing in their kinematics but the wavefunction. It gives the density (in a multidimensional configuration space!) of stuff. To account for the narrowness of that stuff in macroscopic dimensions, the linear Schrödinger equation has to be modified, in this GRW picture by a mathematically prescribed spontaneous collapse mechanism. The big question, in my opinion, is which, if either, of these two precise pictures can be redeveloped in a Lorentz invariant way.Information physics locates Bell's "shifty split" without making GRW ad hoc additions to the linear Schrödinger equation. The "moment" at which the boundary between quantum and classical worlds occurs is the moment that irreversible observable information enters the universe. Although GRW make the wave function collapse, and their mathematics is "precise," they still can not predict exactly when the collapse occurs. It is simply random, with the probability very high in the presence of macroscopic objects. In the information physics solution to the problem of measurement, the timing and location of the Heisenberg "cut" are identified with the interaction between quantum system and classical apparatus that leaves the apparatus in an irreversible stable state providing information to the observer....All historical experience confirms that men might not achieve the possible if they had not, time and time again, reached out for the impossible. (Max Weber) ...we do not know where we are stupid until we stick our necks out. (R. P. Feynman)
GianCarlo Ghirardi on Measurement
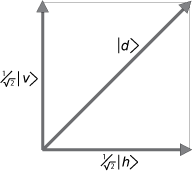
In his elegantly written and nicely illustrated 2005 book, Sneaking a Look at God's Cards, Ghirardi starts his discussion of the measurement problem by noting that the principle of superposition of states means that some observables lack a precise expectation value, so we can speak only of the probability of outcomes. The most characteristic example, he says, is the diagonally polarized photon in a linear combination of vertical and horizontal polarization states discussed in the case of Dirac's Three Polarizers.
| d > = ( 1/√2) | v > + ( 1/√2) | h >
Ghiradi asks whether a macroscopic system can be in such a superposition (think of Schrödinger's live and dead cats), which he describes as
| ? > = ( 1/√2) | here > + ( 1/√2) | there > (15.2)
He says (p.348)
The conclusion is obvious but unsettling: if we admit that the theory (or rather, simply, the superposition principle) has universal validity, and thus governs as well the behavior of macrosystems, it is inescapable to accept that, in principle, macrosystems too can be found in superpositions of states corresponding to precise and different macroscopic properties, with the consequence that these systems cannot legitimately be thought to possess any of these properties. In our specific case, a macroscopic object "is capable of not having the property of being in some place."With this conclusion, Ghirardi begins his discussion of measurement.
For Teachers
For Scholars
Normal | Teacher | Scholar |