The Principle of Superposition
The Schrōdinger equation is
H ψn = Enψn, (1)
where H is the Hamiltonian operator,
ψn is the wave function for state
n, and the
En are the energy eigenvalues for the states.
The eigenfunctions
ψn are orthogonal to each other
where the "delta function"
δ
nm = 1, if
n = m, and = 0, if
n ≠ m. (3)
Once they are normalized, the
ψn form an orthonormal set of
functions (or vectors) which can serve as a basis for
the expansion of an arbitrary wave function
φ
�
|
φ > =
∑ n = 0 n = ∞ cn |
ψn >. (4)
The expansion coefficients are
In the abstract Hilbert space, <
ψn |
φ > is the "projection" of the vector
φ onto the orthogonal axes
ψn of the
ψn "basis" vector set.
The Schrōdinger equation is a
linear
equation. It has no quadratic or
higher power terms, and this introduces the principle
of
superposition of quantum states,
a profound - and for many scientists
and philosophers a disturbing - feature of
quantum mechanics, one that is
impossible
in classical physics.
If
ψa and
ψb are both solutions of equation
(1), then an arbitrary linear combination of
these,
| ψ > = ca | ψa > + cb | ψb >, (6)
with complex coefficients c
a and c
b, is
also a solution.
Born's rule, that waves are probabilities, was actually first suggested by Einstein
Together with Born's probabilistic (statistical) interpretation
of the wave function, the
principle of superposition accounts for
the major mysteries of quantum theory,
some of which we hope to resolve,
or at least reduce, with an objective
(observer-independent) explanation of
irreversible information
creation during quantum processes.
Observable information is critically necessary for
measurements, though observers can come along anytime after the information comes into existence as a consequence of the interaction of a quantum system and a measuring apparatus.
The quantum (discrete) nature of physical
systems results from there generally
being a large number of solutions
ψn
(called eigenfunctions) of equation (1) in
its time independent form, with energy eigenvalues
En.
An example of superposition.
Dirac tells us that a diagonally polarized photon can be represented as a
superposition of vertical and horizontal states, with complex number coefficients that represent "
probability amplitudes." Horizontal and vertical polarization eigenstates are the only "
possibilities," if the measurement apparatus is designed to measure for horizontal or vertical polarization.
Thus,
|
d > = ( 1/√2) |
v > + ( 1/√2) |
h > (10)
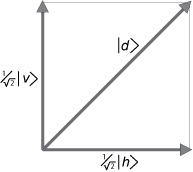
The vectors (wave functions)
v and
h are the appropriate choice of basis vectors, the vector lengths are normalized to unity, and the sum of the squares of the probability amplitudes is also unity. This is the orthonormality condition needed to interpret the (squares of the) wave functions as
probabilities.
When these (in general complex) number coefficients (1/√2) are squared (actually when they are multiplied by their complex conjugates to produce positive real numbers), the numbers (1/2) represent the probabilities of finding the photon in one or the other state, should a measurement be made on an initial state that is diagonally polarized.
Note that if the initial state of the photon had been vertical, its projection along the vertical basis vector would be unity, its projection along the horizontal vector would be zero. Our probability predictions then would be - vertical = 1 (certainty), and horizontal = 0 (also certainty). Quantum physics is not always
uncertain, despite its reputation.
For Teachers
To hide this material, click on the Normal link.
For Scholars
To hide this material, click on the Teacher or Normal link.
Normal |
Teacher |
Scholar