|
Philosophers
Mortimer Adler Rogers Albritton Alexander of Aphrodisias Samuel Alexander William Alston Anaximander G.E.M.Anscombe Anselm Louise Antony Thomas Aquinas Aristotle David Armstrong Harald Atmanspacher Robert Audi Augustine J.L.Austin A.J.Ayer Alexander Bain Mark Balaguer Jeffrey Barrett William Barrett William Belsham Henri Bergson George Berkeley Isaiah Berlin Richard J. Bernstein Bernard Berofsky Robert Bishop Max Black Susanne Bobzien Emil du Bois-Reymond Hilary Bok Laurence BonJour George Boole Émile Boutroux Daniel Boyd F.H.Bradley C.D.Broad Michael Burke Jeremy Butterfield Lawrence Cahoone C.A.Campbell Joseph Keim Campbell Rudolf Carnap Carneades Nancy Cartwright Gregg Caruso Ernst Cassirer David Chalmers Roderick Chisholm Chrysippus Cicero Tom Clark Randolph Clarke Samuel Clarke Anthony Collins Antonella Corradini Diodorus Cronus Jonathan Dancy Donald Davidson Mario De Caro Democritus Daniel Dennett Jacques Derrida René Descartes Richard Double Fred Dretske John Dupré John Earman Laura Waddell Ekstrom Epictetus Epicurus Austin Farrer Herbert Feigl Arthur Fine John Martin Fischer Frederic Fitch Owen Flanagan Luciano Floridi Philippa Foot Alfred Fouilleé Harry Frankfurt Richard L. Franklin Bas van Fraassen Michael Frede Gottlob Frege Peter Geach Edmund Gettier Carl Ginet Alvin Goldman Gorgias Nicholas St. John Green H.Paul Grice Ian Hacking Ishtiyaque Haji Stuart Hampshire W.F.R.Hardie Sam Harris William Hasker R.M.Hare Georg W.F. Hegel Martin Heidegger Heraclitus R.E.Hobart Thomas Hobbes David Hodgson Shadsworth Hodgson Baron d'Holbach Ted Honderich Pamela Huby David Hume Ferenc Huoranszki Frank Jackson William James Lord Kames Robert Kane Immanuel Kant Tomis Kapitan Walter Kaufmann Jaegwon Kim William King Hilary Kornblith Christine Korsgaard Saul Kripke Thomas Kuhn Andrea Lavazza Christoph Lehner Keith Lehrer Gottfried Leibniz Jules Lequyer Leucippus Michael Levin Joseph Levine George Henry Lewes C.I.Lewis David Lewis Peter Lipton C. Lloyd Morgan John Locke Michael Lockwood Arthur O. Lovejoy E. Jonathan Lowe John R. Lucas Lucretius Alasdair MacIntyre Ruth Barcan Marcus Tim Maudlin James Martineau Nicholas Maxwell Storrs McCall Hugh McCann Colin McGinn Michael McKenna Brian McLaughlin John McTaggart Paul E. Meehl Uwe Meixner Alfred Mele Trenton Merricks John Stuart Mill Dickinson Miller G.E.Moore Thomas Nagel Otto Neurath Friedrich Nietzsche John Norton P.H.Nowell-Smith Robert Nozick William of Ockham Timothy O'Connor Parmenides David F. Pears Charles Sanders Peirce Derk Pereboom Steven Pinker U.T.Place Plato Karl Popper Porphyry Huw Price H.A.Prichard Protagoras Hilary Putnam Willard van Orman Quine Frank Ramsey Ayn Rand Michael Rea Thomas Reid Charles Renouvier Nicholas Rescher C.W.Rietdijk Richard Rorty Josiah Royce Bertrand Russell Paul Russell Gilbert Ryle Jean-Paul Sartre Kenneth Sayre T.M.Scanlon Moritz Schlick John Duns Scotus Arthur Schopenhauer John Searle Wilfrid Sellars David Shiang Alan Sidelle Ted Sider Henry Sidgwick Walter Sinnott-Armstrong Peter Slezak J.J.C.Smart Saul Smilansky Michael Smith Baruch Spinoza L. Susan Stebbing Isabelle Stengers George F. Stout Galen Strawson Peter Strawson Eleonore Stump Francisco Suárez Richard Taylor Kevin Timpe Mark Twain Peter Unger Peter van Inwagen Manuel Vargas John Venn Kadri Vihvelin Voltaire G.H. von Wright David Foster Wallace R. Jay Wallace W.G.Ward Ted Warfield Roy Weatherford C.F. von Weizsäcker William Whewell Alfred North Whitehead David Widerker David Wiggins Bernard Williams Timothy Williamson Ludwig Wittgenstein Susan Wolf Scientists David Albert Michael Arbib Walter Baade Bernard Baars Jeffrey Bada Leslie Ballentine Marcello Barbieri Gregory Bateson Horace Barlow John S. Bell Mara Beller Charles Bennett Ludwig von Bertalanffy Susan Blackmore Margaret Boden David Bohm Niels Bohr Ludwig Boltzmann Emile Borel Max Born Satyendra Nath Bose Walther Bothe Jean Bricmont Hans Briegel Leon Brillouin Stephen Brush Henry Thomas Buckle S. H. Burbury Melvin Calvin Donald Campbell Sadi Carnot Anthony Cashmore Eric Chaisson Gregory Chaitin Jean-Pierre Changeux Rudolf Clausius Arthur Holly Compton John Conway Jerry Coyne John Cramer Francis Crick E. P. Culverwell Antonio Damasio Olivier Darrigol Charles Darwin Richard Dawkins Terrence Deacon Lüder Deecke Richard Dedekind Louis de Broglie Stanislas Dehaene Max Delbrück Abraham de Moivre Bernard d'Espagnat Paul Dirac Hans Driesch John Eccles Arthur Stanley Eddington Gerald Edelman Paul Ehrenfest Manfred Eigen Albert Einstein George F. R. Ellis Hugh Everett, III Franz Exner Richard Feynman R. A. Fisher David Foster Joseph Fourier Philipp Frank Steven Frautschi Edward Fredkin Augustin-Jean Fresnel Benjamin Gal-Or Howard Gardner Lila Gatlin Michael Gazzaniga Nicholas Georgescu-Roegen GianCarlo Ghirardi J. Willard Gibbs James J. Gibson Nicolas Gisin Paul Glimcher Thomas Gold A. O. Gomes Brian Goodwin Joshua Greene Dirk ter Haar Jacques Hadamard Mark Hadley Patrick Haggard J. B. S. Haldane Stuart Hameroff Augustin Hamon Sam Harris Ralph Hartley Hyman Hartman Jeff Hawkins John-Dylan Haynes Donald Hebb Martin Heisenberg Werner Heisenberg John Herschel Basil Hiley Art Hobson Jesper Hoffmeyer Don Howard John H. Jackson William Stanley Jevons Roman Jakobson E. T. Jaynes Pascual Jordan Eric Kandel Ruth E. Kastner Stuart Kauffman Martin J. Klein William R. Klemm Christof Koch Simon Kochen Hans Kornhuber Stephen Kosslyn Daniel Koshland Ladislav Kovàč Leopold Kronecker Rolf Landauer Alfred Landé Pierre-Simon Laplace Karl Lashley David Layzer Joseph LeDoux Gerald Lettvin Gilbert Lewis Benjamin Libet David Lindley Seth Lloyd Werner Loewenstein Hendrik Lorentz Josef Loschmidt Alfred Lotka Ernst Mach Donald MacKay Henry Margenau Owen Maroney David Marr Humberto Maturana James Clerk Maxwell Ernst Mayr John McCarthy Warren McCulloch N. David Mermin George Miller Stanley Miller Ulrich Mohrhoff Jacques Monod Vernon Mountcastle Emmy Noether Donald Norman Travis Norsen Alexander Oparin Abraham Pais Howard Pattee Wolfgang Pauli Massimo Pauri Wilder Penfield Roger Penrose Steven Pinker Colin Pittendrigh Walter Pitts Max Planck Susan Pockett Henri Poincaré Daniel Pollen Ilya Prigogine Hans Primas Zenon Pylyshyn Henry Quastler Adolphe Quételet Pasco Rakic Nicolas Rashevsky Lord Rayleigh Frederick Reif Jürgen Renn Giacomo Rizzolati A.A. Roback Emil Roduner Juan Roederer Jerome Rothstein David Ruelle David Rumelhart Robert Sapolsky Tilman Sauer Ferdinand de Saussure Jürgen Schmidhuber Erwin Schrödinger Aaron Schurger Sebastian Seung Thomas Sebeok Franco Selleri Claude Shannon Charles Sherrington Abner Shimony Herbert Simon Dean Keith Simonton Edmund Sinnott B. F. Skinner Lee Smolin Ray Solomonoff Roger Sperry John Stachel Henry Stapp Tom Stonier Antoine Suarez Leo Szilard Max Tegmark Teilhard de Chardin Libb Thims William Thomson (Kelvin) Richard Tolman Giulio Tononi Peter Tse Alan Turing C. S. Unnikrishnan Nico van Kampen Francisco Varela Vlatko Vedral Vladimir Vernadsky Mikhail Volkenstein Heinz von Foerster Richard von Mises John von Neumann Jakob von Uexküll C. H. Waddington John B. Watson Daniel Wegner Steven Weinberg Paul A. Weiss Herman Weyl John Wheeler Jeffrey Wicken Wilhelm Wien Norbert Wiener Eugene Wigner E. O. Wilson Günther Witzany Stephen Wolfram H. Dieter Zeh Semir Zeki Ernst Zermelo Wojciech Zurek Konrad Zuse Fritz Zwicky Presentations Biosemiotics Free Will Mental Causation James Symposium |
The Distinction of Past and Future
Chapter 5 of The Character of Physical Law
Open video in a new window so you can read along with text of the lecture.
It is obvious to everybody that the phenomena of the world are evidently irreversible. I mean things happen that do not happen the other way. You drop a cup and it breaks, and you can sit there a long time waiting for the pieces to come together and jump back into your hand. If you watch the waves of the sea breaking, you can stand there and wait for the great moment when the foam collects together, rises up out of the sea, and falls back farther out from the shore — it would be very pretty!
James Clerk Maxwell was perhaps the first to describe time reversing the world
The demonstration of this in lectures is usually made by having a section of moving picture in which you take a number of phenomena, and run the film backwards, and then wait for all the laughter. The laughter just means this would not happen in the real world. But actually that is a rather weak way to put something which is as obvious and deep as the difference between the past and the future; because even without an experiment our very experiences inside are completely different for past and future. We remember the past, we do not remember the future. We have a different kind of awareness about what might happen than we have of what probably has happened. The past and the future look completely different psychologically, with concepts like memory and apparent freedom of will, in the sense that we feel that we can do something to affect the future, but none of us, or very few of us, believe that there is anything we can do to affect the past. Remorse and regret and hope and so forth are all words which distinguish perfectly obviously the past and the future.
Now if the world of nature is made of atoms, and we too are made of atoms and obey physical laws, the most obvious interpretation of this evident distinction between past and future, and this irreversibility of all phenomena, would be that some laws, some of the motion laws of the atoms are going one way — that the atom laws are not such that they can go either way. There should be somewhere in the works some kind of a principle that uxles only make wuxles and never vice versa, and so the world is turning fron uxley character to wuxley character all the time — and this one-way business of the interactions of things should be the thing that makes the whole phenomena of the world seem to go one way.
But we have not found this yet. That is, in all the laws of physics that we have found so far there does not seem to be any distinction between the past and the future. The moving picture should work the same going both ways, and the physicist who looks at it should not laugh.
Let us take the law of gravitation as our standard example. If I have a sun and a planet, and I start the planet off in some direction, going around the sun, and then I take a moving picture, and run the moving picture backwards and look at it, what happens? The planet goes around the sun, the opposite way of course, keeps on going around in an ellipse. The speed of the planet is such that the area swept out by the radius is always the same in equal times. In fact it just goes exactly the way it ought to go. It cannot be distinguished from going the other way. So the law of gravitation is of such a kind that the direction does not make any difference; if you show any phenomenon involving only gravitation running backwards on a film it will look perfectly satisfactory. You can put it more precisely this way. If all the particles in a more complicated system were to have every one of their speeds reversed suddenly, then the thing would just unwind through all the things that it wound up into. If you have a lot of particles doing something, and then you suddenly reverse the speed, they will completely undo, what they did before.
This is in the law of gravitation, which says that the velocity changes as a result of the forces. If I reverse the time, the forces are not changed, and so the changes in velocity are not altered at corresponding distances. So each velocity then has a succession of alterations made in exactly the reverse of the way that they were made before, and it is easy to prove that the law of gravitation is time-reversible.
The law of electricity and magnetism? Time reversible. The laws of nuclear interaction? Time reversible as far as we can tell. The laws of beta-decay that we talked about at a previous time? Also time reversible? The difficulty of the experiments of a few months ago, which indicate that there is something the matter, some unknown about the laws, suggests the possibility that in fact beta-decay may not also be time reversible, and we shall have to wait for more experiments to see. But at least the following is true. Beta-decay (which may or may not be time reversible) is a very unimportant phenomenon for most ordinary circumstances. The possibility of my talking to you does not depend upon beta-decay, although it does depend on chemical interactions, it depends on electrical forces, not much on nuclear forces at the moment, but it depends also on gravitation. But I am one-sided — I speak, and a voice goes out into the air, and it does not come sucking back into my mouth when I open it — and this irreversibility cannot be hung on the phenomenon of beta-decay. In other words, we believe that most of the ordinary phenomena in the world, which are produced by atomic motions, are according to laws which can be completely reversed. So we will have to look some more to find the explanation of the irreversibility.
If we look at our planets moving around the sun more carefully, we soon find that all is not quite right. For example, the Earth's rotation on its axis is slightly slowing down. It is due to tidal friction, and you can see that friction is something which is obviously irreversible. If I take a heavy weight on the floor, and push it, it will slide and stop. If I stand and wait, it does not suddenly start up and speed up and come into my hand. So the frictional effect seems to be irreversible. But a frictional effect, as we discussed at another time, is the result of the enormous complexity of the interactions of the weight with the wood, the jiggling of the atoms inside. The organized motion of the weight is changed into disorganized, irregular wiggle-waggles of the atoms in the wood. So therefore we should look at the thing more closely.
As a matter of fact, we have here the clue to the apparent irreversibility. I will take a simple example. Suppose we have blue water, with ink, and white water, that is without ink, in a tank, with a little separation, and then we pull out the separation very delicately. The water starts to separate, blue on one side and white on the other side. Wait a while. Gradually the blue mixes up with the white, and after a while the water is 'lake blue', I mean it is sort of fifty-fifty, the colour uniformly distributed throughout. Now if we wait and watch this for a long time, it does not by itself separate. (You could do something to get the blue separated again. You could evaporate the water and condense it somewhere else, and collect the blue dye and dissolve it in half the water, and put the thing back. But while you were doing all that you yourself would be causing irreversible phenomena somewhere else.) By itself it does not go the other way.
That gives us some clue. Let us look at the molecules. Suppose that we take a moving picture of the blue and white water mixing. It will look funny if we run it backwards, because we shall start with uniform water and gradually the thing will separate — it will be obviously nutty. Now we magnify the picture, so that every physicist can watch, atom by atom, to find out what happens irreversibly — where the laws of balance of forward and backward break down. So you start, and you look at the picture. You have atoms of two different kinds (it's ridiculous, but let's call them blue and white) jiggling all the time in thermal motion. If we were to start at the beginning we should have mostly atoms of one kind on one side, and atoms of the other kind on the other side. Now these atoms are jiggling around, billions and billions of them, and if we start them with one kind all on one side, and the other kind on the other side, we see that in their perpetual irregular motions they will get mixed up, and that is why the water becomes more or less uniformly blue.
Let us watch any one collision selected from that picture, and in the moving picture the atoms come together this way and bounce off that way. Now run that section of the film backwards, and you find the pair of molecules moving together the other way and bouncing off this way. And the physicist looks with his keen eye, and measures everything, and says, 'That's all right, that's according to the laws of physics. If two molecules came this way they would bounce this way'. It is reversible. The laws of molecular collision are reversible.
So if you watch too carefully you cannot understand it at all, because every one of the collisions is absolutely reversible, and yet the whole moving picture shows something absurd, which is that in the reversed picture the molecules start in the mixed condition — blue, white, blue, white, blue, white — and as time goes on, through all the collisions, the blue separates from the white. But they cannot do that — it is not natural that the accidents of life should be such that the blues will separate themselves from the whites. And yet if you watch this reversed movie very carefully every collision is O.K.
Well you see that all there is to it is that the irreversibility is caused by the general accidents of life. If you start with a thing that is separated and make irregular changes, it does get more uniform. But if it starts uniform and you make irregular changes, it does not get separated. It could get separated. It is not against the laws of physics that the molecules bounce around so that they separate. It is just unlikely. It would never happen in a million years. And that is the answer. Things are irreversible only in a sense that going one way is likely, but going the other way, although it is possible and is according to the laws of physics, would not happen in a million years. It is just ridiculous to expect that if you sit there long enough the jiggling of the atoms will separate a uniform mixture of ink and water into ink on one side and water on the other.
Now if I had put a box around my experiment, so that there were only four or five molecules of each kind in the box, as time went on they would get mixed up. But I think you could believe that, if you kept watching, in the perpetual irregular collisions of these molecules, after some time — not necessarily a million years, maybe only a year — you would see that, accidentally they would get back more or less to their original state, at least in the sense that if I put a barrier through the middle, all the whites would be on one side and all the blues on the other. It is not impossible. However, the actual objects with which we work have not only four or five blues and whites. They have four or five million, million, million, million, which are all going to get separated like this. And so the apparent irreversibility of nature does not come from the irreversibility of the fundamental physical laws; it comes from the characteristic that if you start with an ordered system, and have the irregularities of nature, the bouncing of molecules, then the thing goes one way.
Therefore the next question is — how did they get ordered in first place? That is to say, why is it possible to start with the ordered? The difficulty is that we start with an ordered thing, and we do not end with an ordered thing. One of the rules of the world is that the thing goes from an ordered condition to a disordered. Incidentally, this word order, like the word disorder, is another of these terms of physics which are not exactly the same as in ordinary life. The order need not be interesting to you as human beings, it is just that there is a definite situation, all on one side and all on the other, or they are mixed up — and that is ordered and disordered.
The question, then, is how the thing gets ordered in the first place, and why, when we look at any ordinary situation, which is only partly ordered, we can conclude that it probably came from one which was more ordered. If I look at a tank of water, in which the water is very dark blue on one side and very clear white on the other, and a sort of bluish colour in between, and I know that the thing has been left alone for twenty or thirty minutes, then I will guess that it got this way because the separation was more complete in the past. If I wait longer, then the blue and white will get more intermixed, and if I know that this thing has been left alone for a sufficiently long time, I can conclude something about the past condition. The fact that it is 'smooth' at the sides can only arise because it was much more satisfactorily separated in the past; because if it were not more satisfactorily separated in the past, in the time since then it would have become more mixed up than it is. It is therefore possible to tell, from the present, something about the past.
In fact physicists do not usually do this much. Physicists like to think that all you have to do is say, 'These are the conditions, now what happens next?' But all our sister sciences have a completely different problem: in fact all the other things that are studied — history, geology, astronomical history — have a problem of this other kind. I find they are able to make predictions of a completely different type from those of a physicist. A physicist says, 'In this condition I'll tell you what will happen next'. But a geologist will say something like this — 'I have dug in the ground and I have found certain kinds of bones. I predict that if you dig in the ground you will find a similar kind of bones'. The historian, although he talks about the past, can do it by talking about the future. When he says that the French Revolution was in 1789, he means that if you look in another book about the French Revolution you will find the same date. What he does is to make a kind of prediction about something that he has never looked at before, documents that have still to be found. He predicts that the documents in which there is something written about Napoleon will coincide with what is written in the other documents. The question is how that is possible — and the only way that is possible is to suggest that the past of the world was more organized in this sense than the present.
Some people have proposed that the way the world became ordered is this. In the beginning the whole universe was just irregular motions, like the mixed water, We saw that if you waited long enough, with very few atoms, the water could have got separated accidentally.
Fluctuations that could reduce the entropy were Ludwig Boltzmann's suggestion
Some physicists (a century ago) suggested that all that has happened is that the world, this system that has been going on and going on, fluctuated. (That is the term used when it gets a little out of the ordinary uniform condition.) It fluctuated, and now we are watching the fluctuation undo itself again. You may say, 'But look how long you would have to wait for such a fluctuation.' I know, but if it did not fluctuate far enough to be able to produce evolution, to be able to produce an intelligent person, we would not have noticed it. So we had to keep waiting until we were alive to notice it — we had to have at least that big a fluctuation. But I believe this theory to be incorrect. I think it is a ridiculous theory for the following reason. If the world were much bigger, and the atoms were all over the place starting from a completely mixed up condition, then if I happened to look only at the atoms in one place, and I found the atoms there separated, I would have no way to conclude that the atoms anywhere else would be separated. In fact if the thing were a fluctuation, and I noticed something odd, the most likely way that it got there would be that there was nothing odd anywhere else. That is, I would have to borrow odds, so to speak, to get the thing lopsided, and there is no use borrowing too much. In the experiment with the blue and white water, when eventually the few molecules in the box became separated, the most likely condition of the rest of the water would still be mixed up. And therefore, although when we look at the stars and we look at the world we see everything is ordered, if there were a fluctuation, the prediction would be that if we looked at a place where we have not looked before, it, would be disordered and a mess. Although the separation of the matter into stars which are hot and space which is cold, which we have seen, could be a fluctuation, then in places where we have not looked we would expect to find that the stars are not separated from space.
And since we always make the prediction that in a place where we have not looked we shall see stars in a similar condition, or find the same statement about Napoleon,
Feynman does not see the cosmic creation process that can produce local reductions in the entropy while the overall entropy increases
or that we shall see bones like the bones that we have seen before, the success of all those sciences indicates that the world did not come from a fluctuation, but came from a condition which was more separated, more organized, in the past than at the present time.
Therefore I think it necessary to add to the physical laws the hypothesis that in the past the universe was more ordered, in the technical sense, than it is today — I think this is the additional statement that is needed to make sense, and to make an understanding of the irreversibility.
That statement itself is of course lopsided in time; it says that something about the past is different from the future. But it comes outside the province of what we ordinarily call physical laws, because we try today to distinguish between the statement of the physical laws which govern the rules by which the universe develops, and the law which states the condition that the world was in in the past. This is considered to be astronomical history — perhaps some day it will also be a part of physical law.
Now there are a number of interesting features of irreversibility which I would like to illustrate. One of them is to see how, exactly, an irreversible machine really works.
Suppose that we build something that we know ought to work only one way — and what I am going to build is a wheel with a ratchet on it — a saw-toothed wheel, with sharp up notches, and relatively slow down notches, all the way round. The wheel is on a shaft, and then there is a little pawl, which is on a pivot and which is held down by a spring (fig. 26).
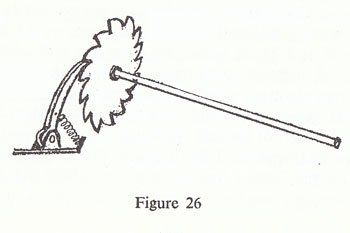 Now the wheel can only turn one way. If you try to turn it the other way, the straight-edged parts of the teeth get jammed against the pawl and it does not go, whereas if you turn it the other way it just goes right over the teeth, snap, snap, snap. (You know the sort of thing: they use them in clocks, and a watch has this kind of thing inside so that you can only wind it one way, and after you have wound it, it holds the spring.) It is completely irreversible in the sense that the wheel can only turn one way.
Now it has been imagined that this irreversible machine, this wheel that can only turn one way, could be used for a very useful and interesting thing. As you know, there is a perpetual irregular motion of molecules, and if you build a very delicate instrument it will always jiggle because it is being bombarded irregularly by the air molecules in the neighbourhood. Well that is very clever, so we will connect the wheel with a shaft that has four vanes, like this (fig. 27).
Now the wheel can only turn one way. If you try to turn it the other way, the straight-edged parts of the teeth get jammed against the pawl and it does not go, whereas if you turn it the other way it just goes right over the teeth, snap, snap, snap. (You know the sort of thing: they use them in clocks, and a watch has this kind of thing inside so that you can only wind it one way, and after you have wound it, it holds the spring.) It is completely irreversible in the sense that the wheel can only turn one way.
Now it has been imagined that this irreversible machine, this wheel that can only turn one way, could be used for a very useful and interesting thing. As you know, there is a perpetual irregular motion of molecules, and if you build a very delicate instrument it will always jiggle because it is being bombarded irregularly by the air molecules in the neighbourhood. Well that is very clever, so we will connect the wheel with a shaft that has four vanes, like this (fig. 27).
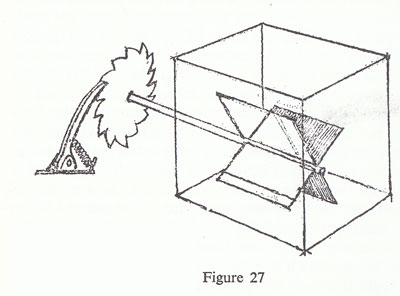 They are in a box of gas, and they are bombarded all the time by the molecules irregularly, so the vanes are pushed sometimes one way, sometimes the other way. But when the vanes are pushed one way the thing gets jammed by the ratchet, and when the vanes are pushed the other way, it goes around, and so we find the wheel perpetually going around, and we have a kind of perpetual motion. That is because the ratchet wheel is irreversible.
But actually we have to look into things in more detail. The way this works is that when the wheel goes one way it lifts the pawl up and then the pawl snaps down against the tooth. Then it will bounce off, and if it is perfectly elastic it will go bounce, bounce, bounce, all the time, and the wheel can just go down and around the other way when the pawl accidentally bounces up. So this will not work unless it is true that when the pawl comes down it sticks, or stops, or bounces and cuts out. If it bounces and cuts out there must be what we call damping, or friction, and in the falling down and bouncing and stopping, which is the only way this will work one-way, heat is generated by the friction, so the wheel will get hotter and hotter. However, when it begins to get quite warm something else happens. Just as there is Brownian motion, or irregular motions, in the gas round the vanes, so whatever this wheel and pawl are made of, the parts that they are made of, are getting hotter, and are beginning to move in a more irregular fashion. The time comes when the wheel is so hot that the pawl is simply jiggling because of the molecular motions of the things inside it, and so it bounces up and down on the wheel because of molecular motion, the same thing as was making the vane turn round. In bouncing up and down on the wheel it is up as much as it is down, and the tooth can go either way. We no longer have a one-way device. As a matter of fact, the thing can be driven backwards! If the wheel is hot and the vane part is cold, the wheel that you thought would go only one way will go the other way, because every time the pawl comes down it comes down on an inclined plane on the toothed wheel, and so pushes the wheel 'backwards'. Then it bounces up again, comes down on another inclined I plane, and so on. So if the wheel is hotter than the vanes it will go the wrong way.
What has this got to do with the temperature of the gas round the vanes? Suppose we did not have that part at all. Then if the wheel is pushed forward by the pawl falling on an inclined plane, the next thing that will happen is that the straight vertical side of the tooth will bounce against the pawl and the wheel will bounce back. In order to prevent the wheel from bouncing back we put a damper on it and put vanes in the air, so it will be slowed down and not bounce freely. Then it will go only one way, but the wrong way, and so it turns out that no matter how you design it, a wheel like this will go one way if one side is hotter and the other way if the other side is hotter. But after there is a heat exchange between the two, and everything is calmed down, so that the vane and the wheel have come to be at the same temperature, it will neither go the one way nor the other on the average. That is the technical way in which the phenomena of nature will go one way as long as they are out of equilibrium, as long as one side is quieter than the other, or one side is bluer than the other.
The conservation of energy would let us think that we have as much energy as we want. Nature never loses or gains energy. Yet the energy of the sea, for example, the thermal motion of all the atoms in the sea, is practically unavailable to us. In order to get that energy organized, herded, to make it available for use, we have to have a difference in temperature, or else we shall find that although the energy is there we cannot make use of it. There is a great difference between energy and availability of energy. The energy of the sea is a large amount, but it is not available to us.
The conservation of energy means that the total energy in the world is kept the same. But in the irregular jigglings that energy can be spread about so uniformly that, in certain circumstances, there is no way to make more go one way than the other — there is no way to control it any more.
I think that by an analogy I can give some idea of the difficulty, in this way. I do not know if you have ever had the experience — I have — of sitting on the beach with several towels, and suddenly a tremendous downpour comes. You pick up the towels as quickly as you can, and run into the bathhouse. Then you start to dry yourself, and you find that this towel is a little wet, but it is drier than you are. You keep drying with this one until you find it is too wet — it is wetting you as much as drying you — and you try another one; and pretty soon you discover a horrible thing — that all the towels are damp and so are you. There is no way to get any drier, even though you have many towels, because there is no difference in some sense between the wetness of the towels and the wetness of yourself. I could invent a kind of quantity which I could call 'ease of removing water'. The towel has the same ease of removing water from it as you have, so when you touch yourself with the towel, as much water comes off the towel on to you as comes from you to the towel. It does not mean there is the same amount of water in the towel as there is on you — a big towel will have more water in it than a little towel — but they have the same dampness. When things get to the same dampness then there is nothing you can do any longer.
Now the water is like the energy, because the total amount of water is not changing. (If the bathhouse door is open and you can run into the sun and get dried out, or find another towel, then you're saved, but suppose everything is closed, and you can't get away from these towels or get any new towels.) In the same way if you imagine a part of the world that is closed, and wait long enough, in the accidents of the world the energy, like the water, will be distributed over all of the parts evenly until there is nothing left of one-way-ness, nothing left of the real interest of the world as we experience it.
Thus in the ratchet and pawl and vanes situation, which is a limited one, in which nothing else is involved, the temperatures gradually become equal on both sides, and the wheel does not go round either one way or the other. In the same way the situation is that if you leave any system long enough it gets the energy thoroughly mixed up in it, and no more energy is really available to do anything.
Incidentally, the thing that corresponds to the dampness or the 'ease of removing water' is called the temperature, and although I say when two things are at the same temperature things get balanced, it does not mean they have the same energy in them; it means that it is just as easy to pick energy off one as to pick it off the other. Temperature is like 'ease of removing energy'. So if you sit them next to each other, nothing apparently happens; they pass energy back and forth equally, but the net result is nothing. So when things have become all of the same temperature, there is no more energy available to do anything. The principle of irreversibility is that if things are at different temperatures and are left to themselves, as time goes on they become more and more at the same temperature, and the availability of energy is perpetually decreasing.
This is another name for what is called the entropy law, which says the entropy is always increasing. But never mind the words; stated the other way, the availability of energy is always decreasing. And that is a characteristic of the world, in the sense that it is due to the chaos of molecular) irregular motions. Things of different temperature, if left to themselves, tend to become of the same temperature. If you have two things at the same temperature, like water on an ordinary stove without a fire under it, the water is not going to freeze and the stove get hot. But if you have a hot stove with ice, it goes the other way. So the one-way-ness is always to the loss of the availability of energy.
That is all I want to say on the subject, but I want to make a few remarks about some characteristics. Here we have an example in which an obvious effect, the irreversibility, is not, an obvious consequence of the laws, but is in fact rather far from the basic laws. It takes a lot of analysis to understand the reason for it. The effect is of first importance in the economy of the world, in the real behaviour of the world in all obvious things. My memory, my characteristics, the difference between past and future, are completely involved in this, and yet the understanding of it is not prima facie available by knowing about the laws. It takes a lot of analysis.
It is often the case that the laws of physics do not have an obvious_ direct relevance to experience, but that they are abstract from experience to varying degrees. In this particular case, the fact that the laws are reversible although the phenomena are not is an example.
There are often great distances between the detailed laws and the main aspects of real phenomena. For example, if you watch a glacier from a distance, and see the big rocks falling into the sea, and the way the ice moves, and so forth, it is not really essential to remember that it is made out of little hexagonal ice crystals. Yet if understood well enough the motion of the glacier is in fact a consequence of the character of the hexagonal ice crystals. But it takes quite a while to understand all the behaviour of the glacier (in fact nobody knows enough about ice yet, no matter how much they've studied the crystal). However the hope is that if we do understand the ice crystal we shall ultimately understand the glacier.
In fact, although we have been talking in these lectures about the fundaments of the physical laws, I must say immediately that one does not, by knowing all the fundamental laws as we know them today, immediately obtain an understanding of anything much. It takes a while, and even then it is only partial. Nature, as a matter of fact, seems to be so designed that the most important things in the real world appear to be a kind of complicated accidental result of a lot of laws.
To give an example, nuclei, which involve several nuclear particles, protons and neutrons, are very complicated. They have what we call energy levels, they can sit in states or conditions of different energy values, and various nuclei have various energy levels. And it's a complicated mathematical problem, which we can only partly solve, to find the position of the energy levels. The exact position of the levels is obviously a consequence of an enormous complexity and therefore there is no particular mystery about the fact that nitrogen, with 15 particles inside, happens to have a level at 2.4 million volts, and another level at 7.1. and so on. But
the remarkable thing about nature is that the whole universe in its character depends upon precisely the position of one particular level in one particular nucleus. In the carbon12 nucleus, it so happens, there is a level at 7.82 million volts. And that makes all the difference in the world.
The situation is the following. If we start with hydrogen, and it appears that at the beginning the world was practically all hydrogen, then as the hydrogen comes together under gravity and gets hotter, nuclear reactions can take place, and it can form helium, and then the helium can combine only partially with the hydrogen and produce a few more elements, a little heavier. But these heavier elements disintegrate right away back into helium. Therefore for a while there was a great mystery about where all the other elements in the world came from, because starting with hydrogen the cooking processes inside the stars would not make much more than helium and less than half a dozen other elements. Faced with this problem, Professors Hoyle and Salpeter [Fred Hoyle, British astronomer, Cambridge. Edwin Salpeter, American physicist, Cornell University] said that there is one way out. If three helium atoms could come together to form carbon, we can easily calculate how often that should happen in a star. And it turns out that it should never happen, except for one possible accident — if there happened to be an energy level at 7.82 million volts in carbon, then the three helium atoms would come together and before they came apart, would stay together a little longer on the average than they would do if there were no level at 7.82. And staying there a little longer, there would be enough time for something else to happen, and to make other elements. If there was a level at 7.82 million volts in carbon, then we could understand where all the other elements in the periodic table came from. And so, by a backhanded, upside-down argument, it was predicted that there is in carbon a level at 7.82 million volts; and experiments in the laboratory showed that indeed there is. Therefore the existence in the world of all these other elements is very closely related to the fact that there is this particular level in carbon. But the position of this particular level in carbon seems to us, knowing the physical laws, to be a very complicated accident of 12 complicated particles interacting. This example is an excellent illustration of the fact that an understanding of the physical laws does not necessarily give you an understanding of things of significance in the world in any direct way. The details of real experience are often very far from the fundamental laws.
We have a way of discussing the world, when we talk of it at various hierarchies, or levels. Now I do not mean to be very precise, dividing the world into definite levels, but I will indicate, by describing a set of ideas, what I mean by hierarchies of ideas.
For example, at one end we have the fundamental laws of physics. Then we invent other terms for concepts which are approximate, which have, we believe, their ultimate explanation in terms of the fundamental laws. For instance, 'heat'. Heat is supposed to be jiggling, and the word for a hot thing is just the word for a mass of atoms which are jiggling. But for a while, if we are talking about heat, we sometimes forget about the atoms jiggling — just as when we talk about the glacier we do not always think of the hexagonal ice and the snowflakes which originally fell. Another example of the same thing is a salt crystal. Looked at fundamentally it is a lot of protons, neutrons, and electrons; but we have this concept 'salt crystal', which carries a whole pattern already of fundamental interactions. An idea like pressure is the same.
Now if we go higher up from this, in another level we have properties of substances — like 'refractive index', how light is bent when it goes through something; or 'surface tension', the fact that water tends to pull itself together, both of which are described by numbers. I remind you that we have to go through several laws down to find out that it is the pull of the atoms, and so on. But we still say 'surface tension', and do not always worry, when discussing surface tension, about the inner workings.
On, up in the hierarchy. With the water we have waves and we have a thing like a storm, the word 'storm' which represents an enormous mass of phenomena, or a 'sun spot' or 'star', which is an accumulation of things. And it is nu worth while always to think of it way back. In fact we cannot, because the higher up we go the more steps we have in between, each one of which is a little weak. We have not thought them all through yet.
As we go up in this hierarchy of complexity, we get tc things like muscle twitch, or nerve impulse, which is an enormously complicated thing in the physical world, involving an organization of matter in a very elaborate complexity. Then come things like 'frog'.
And then we go on, and we come to words and concepts like 'man', and 'history', or 'political expediency', and so forth, a series of concepts which we use to understand things at an ever higher level.
And going on, we come to things like evil, and beauty, and hope...
Which end is nearer to God; if I may use a religious metaphor. Beauty and hope, or the fundamental laws ? I think that the right way, of course, is to say that what we have to look at is the whole structural interconnection of the thing; and that all the sciences, and not just the sciences but all the efforts of intellectual kinds, are an endeavour to see the connections of the hierarchies, to connect beauty to history, to connect history to man's psychology, man's psychology to the working of the brain, the brain to the neural impulse, the neural impulse to the chemistry, and so forth, up and down, both ways. And today we cannot, and it is no use making believe that we can, draw carefully a line all the way from one end of this thing to the other, because we have only just begun to see that there is this relative hierarchy.
And I do not think either end is nearer to God. To stand at either end, and to walk off that end of the pier only, hoping that out in that direction is the complete understanding, is a mistake. And to stand with evil and beauty and hope, or to stand with the fundamental laws, hoping that way to get a deep understanding of the whole world, with that aspect alone, is a mistake. It is not sensible for the ones who specialize at one end, and the ones who specialize at the other end, to have such disregard for each other. (They don't actually, but people say they do.) The great mass of workers in between, connecting one step to another, are improving all the time our understanding of the world, both from working at the ends and working in the middle, and in that way we are gradually understanding this tremendous world of interconnecting hierarchies.
They are in a box of gas, and they are bombarded all the time by the molecules irregularly, so the vanes are pushed sometimes one way, sometimes the other way. But when the vanes are pushed one way the thing gets jammed by the ratchet, and when the vanes are pushed the other way, it goes around, and so we find the wheel perpetually going around, and we have a kind of perpetual motion. That is because the ratchet wheel is irreversible.
But actually we have to look into things in more detail. The way this works is that when the wheel goes one way it lifts the pawl up and then the pawl snaps down against the tooth. Then it will bounce off, and if it is perfectly elastic it will go bounce, bounce, bounce, all the time, and the wheel can just go down and around the other way when the pawl accidentally bounces up. So this will not work unless it is true that when the pawl comes down it sticks, or stops, or bounces and cuts out. If it bounces and cuts out there must be what we call damping, or friction, and in the falling down and bouncing and stopping, which is the only way this will work one-way, heat is generated by the friction, so the wheel will get hotter and hotter. However, when it begins to get quite warm something else happens. Just as there is Brownian motion, or irregular motions, in the gas round the vanes, so whatever this wheel and pawl are made of, the parts that they are made of, are getting hotter, and are beginning to move in a more irregular fashion. The time comes when the wheel is so hot that the pawl is simply jiggling because of the molecular motions of the things inside it, and so it bounces up and down on the wheel because of molecular motion, the same thing as was making the vane turn round. In bouncing up and down on the wheel it is up as much as it is down, and the tooth can go either way. We no longer have a one-way device. As a matter of fact, the thing can be driven backwards! If the wheel is hot and the vane part is cold, the wheel that you thought would go only one way will go the other way, because every time the pawl comes down it comes down on an inclined plane on the toothed wheel, and so pushes the wheel 'backwards'. Then it bounces up again, comes down on another inclined I plane, and so on. So if the wheel is hotter than the vanes it will go the wrong way.
What has this got to do with the temperature of the gas round the vanes? Suppose we did not have that part at all. Then if the wheel is pushed forward by the pawl falling on an inclined plane, the next thing that will happen is that the straight vertical side of the tooth will bounce against the pawl and the wheel will bounce back. In order to prevent the wheel from bouncing back we put a damper on it and put vanes in the air, so it will be slowed down and not bounce freely. Then it will go only one way, but the wrong way, and so it turns out that no matter how you design it, a wheel like this will go one way if one side is hotter and the other way if the other side is hotter. But after there is a heat exchange between the two, and everything is calmed down, so that the vane and the wheel have come to be at the same temperature, it will neither go the one way nor the other on the average. That is the technical way in which the phenomena of nature will go one way as long as they are out of equilibrium, as long as one side is quieter than the other, or one side is bluer than the other.
The conservation of energy would let us think that we have as much energy as we want. Nature never loses or gains energy. Yet the energy of the sea, for example, the thermal motion of all the atoms in the sea, is practically unavailable to us. In order to get that energy organized, herded, to make it available for use, we have to have a difference in temperature, or else we shall find that although the energy is there we cannot make use of it. There is a great difference between energy and availability of energy. The energy of the sea is a large amount, but it is not available to us.
The conservation of energy means that the total energy in the world is kept the same. But in the irregular jigglings that energy can be spread about so uniformly that, in certain circumstances, there is no way to make more go one way than the other — there is no way to control it any more.
I think that by an analogy I can give some idea of the difficulty, in this way. I do not know if you have ever had the experience — I have — of sitting on the beach with several towels, and suddenly a tremendous downpour comes. You pick up the towels as quickly as you can, and run into the bathhouse. Then you start to dry yourself, and you find that this towel is a little wet, but it is drier than you are. You keep drying with this one until you find it is too wet — it is wetting you as much as drying you — and you try another one; and pretty soon you discover a horrible thing — that all the towels are damp and so are you. There is no way to get any drier, even though you have many towels, because there is no difference in some sense between the wetness of the towels and the wetness of yourself. I could invent a kind of quantity which I could call 'ease of removing water'. The towel has the same ease of removing water from it as you have, so when you touch yourself with the towel, as much water comes off the towel on to you as comes from you to the towel. It does not mean there is the same amount of water in the towel as there is on you — a big towel will have more water in it than a little towel — but they have the same dampness. When things get to the same dampness then there is nothing you can do any longer.
Now the water is like the energy, because the total amount of water is not changing. (If the bathhouse door is open and you can run into the sun and get dried out, or find another towel, then you're saved, but suppose everything is closed, and you can't get away from these towels or get any new towels.) In the same way if you imagine a part of the world that is closed, and wait long enough, in the accidents of the world the energy, like the water, will be distributed over all of the parts evenly until there is nothing left of one-way-ness, nothing left of the real interest of the world as we experience it.
Thus in the ratchet and pawl and vanes situation, which is a limited one, in which nothing else is involved, the temperatures gradually become equal on both sides, and the wheel does not go round either one way or the other. In the same way the situation is that if you leave any system long enough it gets the energy thoroughly mixed up in it, and no more energy is really available to do anything.
Incidentally, the thing that corresponds to the dampness or the 'ease of removing water' is called the temperature, and although I say when two things are at the same temperature things get balanced, it does not mean they have the same energy in them; it means that it is just as easy to pick energy off one as to pick it off the other. Temperature is like 'ease of removing energy'. So if you sit them next to each other, nothing apparently happens; they pass energy back and forth equally, but the net result is nothing. So when things have become all of the same temperature, there is no more energy available to do anything. The principle of irreversibility is that if things are at different temperatures and are left to themselves, as time goes on they become more and more at the same temperature, and the availability of energy is perpetually decreasing.
This is another name for what is called the entropy law, which says the entropy is always increasing. But never mind the words; stated the other way, the availability of energy is always decreasing. And that is a characteristic of the world, in the sense that it is due to the chaos of molecular) irregular motions. Things of different temperature, if left to themselves, tend to become of the same temperature. If you have two things at the same temperature, like water on an ordinary stove without a fire under it, the water is not going to freeze and the stove get hot. But if you have a hot stove with ice, it goes the other way. So the one-way-ness is always to the loss of the availability of energy.
That is all I want to say on the subject, but I want to make a few remarks about some characteristics. Here we have an example in which an obvious effect, the irreversibility, is not, an obvious consequence of the laws, but is in fact rather far from the basic laws. It takes a lot of analysis to understand the reason for it. The effect is of first importance in the economy of the world, in the real behaviour of the world in all obvious things. My memory, my characteristics, the difference between past and future, are completely involved in this, and yet the understanding of it is not prima facie available by knowing about the laws. It takes a lot of analysis.
It is often the case that the laws of physics do not have an obvious_ direct relevance to experience, but that they are abstract from experience to varying degrees. In this particular case, the fact that the laws are reversible although the phenomena are not is an example.
There are often great distances between the detailed laws and the main aspects of real phenomena. For example, if you watch a glacier from a distance, and see the big rocks falling into the sea, and the way the ice moves, and so forth, it is not really essential to remember that it is made out of little hexagonal ice crystals. Yet if understood well enough the motion of the glacier is in fact a consequence of the character of the hexagonal ice crystals. But it takes quite a while to understand all the behaviour of the glacier (in fact nobody knows enough about ice yet, no matter how much they've studied the crystal). However the hope is that if we do understand the ice crystal we shall ultimately understand the glacier.
In fact, although we have been talking in these lectures about the fundaments of the physical laws, I must say immediately that one does not, by knowing all the fundamental laws as we know them today, immediately obtain an understanding of anything much. It takes a while, and even then it is only partial. Nature, as a matter of fact, seems to be so designed that the most important things in the real world appear to be a kind of complicated accidental result of a lot of laws.
To give an example, nuclei, which involve several nuclear particles, protons and neutrons, are very complicated. They have what we call energy levels, they can sit in states or conditions of different energy values, and various nuclei have various energy levels. And it's a complicated mathematical problem, which we can only partly solve, to find the position of the energy levels. The exact position of the levels is obviously a consequence of an enormous complexity and therefore there is no particular mystery about the fact that nitrogen, with 15 particles inside, happens to have a level at 2.4 million volts, and another level at 7.1. and so on. But
the remarkable thing about nature is that the whole universe in its character depends upon precisely the position of one particular level in one particular nucleus. In the carbon12 nucleus, it so happens, there is a level at 7.82 million volts. And that makes all the difference in the world.
The situation is the following. If we start with hydrogen, and it appears that at the beginning the world was practically all hydrogen, then as the hydrogen comes together under gravity and gets hotter, nuclear reactions can take place, and it can form helium, and then the helium can combine only partially with the hydrogen and produce a few more elements, a little heavier. But these heavier elements disintegrate right away back into helium. Therefore for a while there was a great mystery about where all the other elements in the world came from, because starting with hydrogen the cooking processes inside the stars would not make much more than helium and less than half a dozen other elements. Faced with this problem, Professors Hoyle and Salpeter [Fred Hoyle, British astronomer, Cambridge. Edwin Salpeter, American physicist, Cornell University] said that there is one way out. If three helium atoms could come together to form carbon, we can easily calculate how often that should happen in a star. And it turns out that it should never happen, except for one possible accident — if there happened to be an energy level at 7.82 million volts in carbon, then the three helium atoms would come together and before they came apart, would stay together a little longer on the average than they would do if there were no level at 7.82. And staying there a little longer, there would be enough time for something else to happen, and to make other elements. If there was a level at 7.82 million volts in carbon, then we could understand where all the other elements in the periodic table came from. And so, by a backhanded, upside-down argument, it was predicted that there is in carbon a level at 7.82 million volts; and experiments in the laboratory showed that indeed there is. Therefore the existence in the world of all these other elements is very closely related to the fact that there is this particular level in carbon. But the position of this particular level in carbon seems to us, knowing the physical laws, to be a very complicated accident of 12 complicated particles interacting. This example is an excellent illustration of the fact that an understanding of the physical laws does not necessarily give you an understanding of things of significance in the world in any direct way. The details of real experience are often very far from the fundamental laws.
We have a way of discussing the world, when we talk of it at various hierarchies, or levels. Now I do not mean to be very precise, dividing the world into definite levels, but I will indicate, by describing a set of ideas, what I mean by hierarchies of ideas.
For example, at one end we have the fundamental laws of physics. Then we invent other terms for concepts which are approximate, which have, we believe, their ultimate explanation in terms of the fundamental laws. For instance, 'heat'. Heat is supposed to be jiggling, and the word for a hot thing is just the word for a mass of atoms which are jiggling. But for a while, if we are talking about heat, we sometimes forget about the atoms jiggling — just as when we talk about the glacier we do not always think of the hexagonal ice and the snowflakes which originally fell. Another example of the same thing is a salt crystal. Looked at fundamentally it is a lot of protons, neutrons, and electrons; but we have this concept 'salt crystal', which carries a whole pattern already of fundamental interactions. An idea like pressure is the same.
Now if we go higher up from this, in another level we have properties of substances — like 'refractive index', how light is bent when it goes through something; or 'surface tension', the fact that water tends to pull itself together, both of which are described by numbers. I remind you that we have to go through several laws down to find out that it is the pull of the atoms, and so on. But we still say 'surface tension', and do not always worry, when discussing surface tension, about the inner workings.
On, up in the hierarchy. With the water we have waves and we have a thing like a storm, the word 'storm' which represents an enormous mass of phenomena, or a 'sun spot' or 'star', which is an accumulation of things. And it is nu worth while always to think of it way back. In fact we cannot, because the higher up we go the more steps we have in between, each one of which is a little weak. We have not thought them all through yet.
As we go up in this hierarchy of complexity, we get tc things like muscle twitch, or nerve impulse, which is an enormously complicated thing in the physical world, involving an organization of matter in a very elaborate complexity. Then come things like 'frog'.
And then we go on, and we come to words and concepts like 'man', and 'history', or 'political expediency', and so forth, a series of concepts which we use to understand things at an ever higher level.
And going on, we come to things like evil, and beauty, and hope...
Which end is nearer to God; if I may use a religious metaphor. Beauty and hope, or the fundamental laws ? I think that the right way, of course, is to say that what we have to look at is the whole structural interconnection of the thing; and that all the sciences, and not just the sciences but all the efforts of intellectual kinds, are an endeavour to see the connections of the hierarchies, to connect beauty to history, to connect history to man's psychology, man's psychology to the working of the brain, the brain to the neural impulse, the neural impulse to the chemistry, and so forth, up and down, both ways. And today we cannot, and it is no use making believe that we can, draw carefully a line all the way from one end of this thing to the other, because we have only just begun to see that there is this relative hierarchy.
And I do not think either end is nearer to God. To stand at either end, and to walk off that end of the pier only, hoping that out in that direction is the complete understanding, is a mistake. And to stand with evil and beauty and hope, or to stand with the fundamental laws, hoping that way to get a deep understanding of the whole world, with that aspect alone, is a mistake. It is not sensible for the ones who specialize at one end, and the ones who specialize at the other end, to have such disregard for each other. (They don't actually, but people say they do.) The great mass of workers in between, connecting one step to another, are improving all the time our understanding of the world, both from working at the ends and working in the middle, and in that way we are gradually understanding this tremendous world of interconnecting hierarchies.
See also Probability and Uncertainty - the Quantum Mechanical View of Nature For Teachers
For Scholars
|