|
Philosophers
Mortimer Adler Rogers Albritton Alexander of Aphrodisias Samuel Alexander William Alston Anaximander G.E.M.Anscombe Anselm Louise Antony Thomas Aquinas Aristotle David Armstrong Harald Atmanspacher Robert Audi Augustine J.L.Austin A.J.Ayer Alexander Bain Mark Balaguer Jeffrey Barrett William Barrett William Belsham Henri Bergson George Berkeley Isaiah Berlin Richard J. Bernstein Bernard Berofsky Robert Bishop Max Black Susanne Bobzien Emil du Bois-Reymond Hilary Bok Laurence BonJour George Boole Émile Boutroux Daniel Boyd F.H.Bradley C.D.Broad Michael Burke Jeremy Butterfield Lawrence Cahoone C.A.Campbell Joseph Keim Campbell Rudolf Carnap Carneades Nancy Cartwright Gregg Caruso Ernst Cassirer David Chalmers Roderick Chisholm Chrysippus Cicero Tom Clark Randolph Clarke Samuel Clarke Anthony Collins Antonella Corradini Diodorus Cronus Jonathan Dancy Donald Davidson Mario De Caro Democritus Daniel Dennett Jacques Derrida René Descartes Richard Double Fred Dretske John Earman Laura Waddell Ekstrom Epictetus Epicurus Austin Farrer Herbert Feigl Arthur Fine John Martin Fischer Frederic Fitch Owen Flanagan Luciano Floridi Philippa Foot Alfred Fouilleé Harry Frankfurt Richard L. Franklin Bas van Fraassen Michael Frede Gottlob Frege Peter Geach Edmund Gettier Carl Ginet Alvin Goldman Gorgias Nicholas St. John Green H.Paul Grice Ian Hacking Ishtiyaque Haji Stuart Hampshire W.F.R.Hardie Sam Harris William Hasker R.M.Hare Georg W.F. Hegel Martin Heidegger Heraclitus R.E.Hobart Thomas Hobbes David Hodgson Shadsworth Hodgson Baron d'Holbach Ted Honderich Pamela Huby David Hume Ferenc Huoranszki Frank Jackson William James Lord Kames Robert Kane Immanuel Kant Tomis Kapitan Walter Kaufmann Jaegwon Kim William King Hilary Kornblith Christine Korsgaard Saul Kripke Thomas Kuhn Andrea Lavazza James Ladyman Christoph Lehner Keith Lehrer Gottfried Leibniz Jules Lequyer Leucippus Michael Levin Joseph Levine George Henry Lewes C.I.Lewis David Lewis Peter Lipton C. Lloyd Morgan John Locke Michael Lockwood Arthur O. Lovejoy E. Jonathan Lowe John R. Lucas Lucretius Alasdair MacIntyre Ruth Barcan Marcus Tim Maudlin James Martineau Nicholas Maxwell Storrs McCall Hugh McCann Colin McGinn Michael McKenna Brian McLaughlin John McTaggart Paul E. Meehl Uwe Meixner Alfred Mele Trenton Merricks John Stuart Mill Dickinson Miller G.E.Moore Ernest Nagel Thomas Nagel Otto Neurath Friedrich Nietzsche John Norton P.H.Nowell-Smith Robert Nozick William of Ockham Timothy O'Connor Parmenides David F. Pears Charles Sanders Peirce Derk Pereboom Steven Pinker U.T.Place Plato Karl Popper Porphyry Huw Price H.A.Prichard Protagoras Hilary Putnam Willard van Orman Quine Frank Ramsey Ayn Rand Michael Rea Thomas Reid Charles Renouvier Nicholas Rescher C.W.Rietdijk Richard Rorty Josiah Royce Bertrand Russell Paul Russell Gilbert Ryle Jean-Paul Sartre Kenneth Sayre T.M.Scanlon Moritz Schlick John Duns Scotus Arthur Schopenhauer John Searle Wilfrid Sellars David Shiang Alan Sidelle Ted Sider Henry Sidgwick Walter Sinnott-Armstrong Peter Slezak J.J.C.Smart Saul Smilansky Michael Smith Baruch Spinoza L. Susan Stebbing Isabelle Stengers George F. Stout Galen Strawson Peter Strawson Eleonore Stump Francisco Suárez Richard Taylor Kevin Timpe Mark Twain Peter Unger Peter van Inwagen Manuel Vargas John Venn Kadri Vihvelin Voltaire G.H. von Wright David Foster Wallace R. Jay Wallace W.G.Ward Ted Warfield Roy Weatherford C.F. von Weizsäcker William Whewell Alfred North Whitehead David Widerker David Wiggins Bernard Williams Timothy Williamson Ludwig Wittgenstein Susan Wolf Scientists David Albert Michael Arbib Walter Baade Bernard Baars Jeffrey Bada Leslie Ballentine Marcello Barbieri Gregory Bateson Horace Barlow John S. Bell Mara Beller Charles Bennett Ludwig von Bertalanffy Susan Blackmore Margaret Boden David Bohm Niels Bohr Ludwig Boltzmann Emile Borel Max Born Satyendra Nath Bose Walther Bothe Jean Bricmont Hans Briegel Leon Brillouin Stephen Brush Henry Thomas Buckle S. H. Burbury Melvin Calvin Donald Campbell Sadi Carnot Anthony Cashmore Eric Chaisson Gregory Chaitin Jean-Pierre Changeux Rudolf Clausius Arthur Holly Compton John Conway Simon Conway-Morris Jerry Coyne John Cramer Francis Crick E. P. Culverwell Antonio Damasio Olivier Darrigol Charles Darwin Richard Dawkins Terrence Deacon Lüder Deecke Richard Dedekind Louis de Broglie Stanislas Dehaene Max Delbrück Abraham de Moivre Bernard d'Espagnat Paul Dirac Hans Driesch John Dupré John Eccles Arthur Stanley Eddington Gerald Edelman Paul Ehrenfest Manfred Eigen Albert Einstein George F. R. Ellis Hugh Everett, III Franz Exner Richard Feynman R. A. Fisher David Foster Joseph Fourier Philipp Frank Steven Frautschi Edward Fredkin Augustin-Jean Fresnel Benjamin Gal-Or Howard Gardner Lila Gatlin Michael Gazzaniga Nicholas Georgescu-Roegen GianCarlo Ghirardi J. Willard Gibbs James J. Gibson Nicolas Gisin Paul Glimcher Thomas Gold A. O. Gomes Brian Goodwin Joshua Greene Dirk ter Haar Jacques Hadamard Mark Hadley Patrick Haggard J. B. S. Haldane Stuart Hameroff Augustin Hamon Sam Harris Ralph Hartley Hyman Hartman Jeff Hawkins John-Dylan Haynes Donald Hebb Martin Heisenberg Werner Heisenberg Grete Hermann John Herschel Basil Hiley Art Hobson Jesper Hoffmeyer Don Howard John H. Jackson William Stanley Jevons Roman Jakobson E. T. Jaynes Pascual Jordan Eric Kandel Ruth E. Kastner Stuart Kauffman Martin J. Klein William R. Klemm Christof Koch Simon Kochen Hans Kornhuber Stephen Kosslyn Daniel Koshland Ladislav Kovàč Leopold Kronecker Rolf Landauer Alfred Landé Pierre-Simon Laplace Karl Lashley David Layzer Joseph LeDoux Gerald Lettvin Gilbert Lewis Benjamin Libet David Lindley Seth Lloyd Werner Loewenstein Hendrik Lorentz Josef Loschmidt Alfred Lotka Ernst Mach Donald MacKay Henry Margenau Owen Maroney David Marr Humberto Maturana James Clerk Maxwell Ernst Mayr John McCarthy Warren McCulloch N. David Mermin George Miller Stanley Miller Ulrich Mohrhoff Jacques Monod Vernon Mountcastle Emmy Noether Donald Norman Travis Norsen Alexander Oparin Abraham Pais Howard Pattee Wolfgang Pauli Massimo Pauri Wilder Penfield Roger Penrose Steven Pinker Colin Pittendrigh Walter Pitts Max Planck Susan Pockett Henri Poincaré Daniel Pollen Ilya Prigogine Hans Primas Zenon Pylyshyn Henry Quastler Adolphe Quételet Pasco Rakic Nicolas Rashevsky Lord Rayleigh Frederick Reif Jürgen Renn Giacomo Rizzolati A.A. Roback Emil Roduner Juan Roederer Jerome Rothstein David Ruelle David Rumelhart Robert Sapolsky Tilman Sauer Ferdinand de Saussure Jürgen Schmidhuber Erwin Schrödinger Aaron Schurger Sebastian Seung Thomas Sebeok Franco Selleri Claude Shannon Charles Sherrington Abner Shimony Herbert Simon Dean Keith Simonton Edmund Sinnott B. F. Skinner Lee Smolin Ray Solomonoff Roger Sperry John Stachel Henry Stapp Tom Stonier Antoine Suarez Leo Szilard Max Tegmark Teilhard de Chardin Libb Thims William Thomson (Kelvin) Richard Tolman Giulio Tononi Peter Tse Alan Turing C. S. Unnikrishnan Nico van Kampen Francisco Varela Vlatko Vedral Vladimir Vernadsky Mikhail Volkenstein Heinz von Foerster Richard von Mises John von Neumann Jakob von Uexküll C. H. Waddington James D. Watson John B. Watson Daniel Wegner Steven Weinberg Paul A. Weiss Herman Weyl John Wheeler Jeffrey Wicken Wilhelm Wien Norbert Wiener Eugene Wigner E. O. Wilson Günther Witzany Stephen Wolfram H. Dieter Zeh Semir Zeki Ernst Zermelo Wojciech Zurek Konrad Zuse Fritz Zwicky Presentations Biosemiotics Free Will Mental Causation James Symposium |
Jerome Rothstein
Jerome Rothstein was a physicist who wrote on the connection between information and "system organization." He imagined physical systems called "well-informed heat engines" that could (within limits) predict their future behaviors, and so answer some questions like the problem of free will, purposes, causes, origins, and ultimate destinies.
Some of these questions he found to be "undecidable," and he related the undecidability to the absolute limits set by the second law of thermodynamics. In a 1964 Philosophy of Science article "Thermodynamics and Some Undecidable Physical Questions," he wrote
By a well-informed heat engine we mean a machine and power source with measuring apparatus to determine, at least partially, the state of its environment and itself, effector apparatus to perform operations on its environment and on itself, and internal programming, computers, and control circuitry whereby it can carry out particular patterns of behavior in response to the information input through the measuring apparatus and the information and programs stored in its memory. A version of the problem of free will appropriate to a well-informed heat engine is that of determining whether the engine can predict its own future on the basis of measurements it can perform, where knowledge of the dynamical laws governing the engine and its environment is stored in the memory. We have shown that the machine cannot determine its future for all time within the accuracy permitted by the measurements it can perform, and that the impossibility of its doing so is equivalent to the second law of thermodynamics. We can interpret this result as meaning that the heat engine can never decide whether its fate is completely determined in advance, or not, the latter situation being what we may call "free will." From an operational point of view, relative to the universe of the heat engine, the question of free will versus determinism is incapable of being answered and thus, like the absolute space and time of pre-relativity days, poses a pseudo-problem no longer of physical importance.In 1951 Rothstein wrote a survey article for Science on "Information, Measurement, and Quantum Mechanics." It was a short history of the concepts of entropy and information, it discussed information in physics and the connection between physical and informational entropies, and it demonstrated a logical identity between the problem of measurement and the problem of communication. Rothstein described a profound analogy between communication and measurement that we can call Rothstein's Analogy. It is a version of Claude Shannon's communications diagram, where Shannon's labels are supplemented by the analogous steps in a physical measurement. 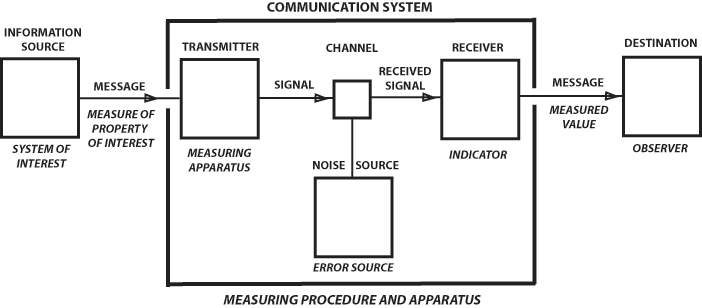
Information, Measurement, and Quantum Mechanics
RECENT DEVELOPMENTS IN COMMUNICATION THEORY use a function
called the entropy, which gives a measure of the quantity of information carried by a message. This name was chosen because of the similarity in mathematical form between informational entropy and the entropy of statistical mechanics. Increasing attention is being devoted to the connection between information and physical entropy (1-9), Maxwell's demon providing a typical opportunity for the concepts to interact.
It is the purpose of this paper to present a short history of the concepts of entropy and information, to discuss information in physics and the connection between physical and informational entropies, and to demonstrate the logical identity of the problem of measurement and the problem of communication. Various implications for statistical mechanics, thermodynamics, and quantum mechanics, as well as the possible relevance of generalized entropy for biology, will he briefly considered. Paradoxes and questions of interpretation in quantum mechanics, as well as reality, causality, and the completeness of quantum mechanics, will also be briefly examined from an informational viewpoint.
INFORMATION AND ENTROPY
Boltzmann's discovery of a statistical explanation for entropy will always rank as one of the great achievements in theoretical physics. By its use, he was able to show how classical mechanics, applied to billiard-ball molecules or to more complicated mechanical systems, could explain the laws of thermodynamics. After much controversy (arising from the reversibility of mechanics as opposed to the irreversibility of thermodynamics), during which the logical basis of the theory was recast, the main results were firmly based on the abstract theory of measurable sets. The function Boltzmann introduced depends on how molecular positions and momenta range over their possible values (for fixed total energy), becoming larger with increasing randomness or spread in these molecular parameters, and decreasing to zero for a perfectly sharp distribution. Entropy often came to be described in later years as a measure of disorder, randomness, or chaos. Boltzmann himself saw later that statistical entropy could be interpreted as a measure of missing information.
A number of different definitions of entropy have been given, the differences residing chiefly in the employment of different approximations or in choosing a classical or quantal approach. Boltzmann's classical and Planck's quantal definitions, for example, are, respectively,
S = —k ∫ f log f dτ,
Here k is Boltzmann's constant, f the molecular distribution function over coordinates and momenta, dτ an element of phase space, and P the number of independent wave functions consistent with the known energy of the system and other general information, like requirements of symmetry or accessibility.
Even before maturation of the entropy concept, Maxwell pointed out that a little demon who could "see" individual molecules would be able to let fast ones through a trap door and keep slow ones out. A specimen of gas at uniform temperature could thereby be divided into low and high temperature portions, separated by a partition. A heat engine working between them would then constitute a perpetuum mobile of the second kind. Szilard (1), in considering this problem, showed that the second law of thermodynamics could be saved only if the demon paid for the information on which he acted with entropy increase elsewhere. If, like physicists, the demon gets his information by means of measuring apparatus, then the price is paid in full. He was led to ascribe a thermodynamical equivalent to an item of information. If one knew in which of two equal volumes a molecule was to be found, he showed that the entropy could be reduced by k log 2.
Hartley (2), considering the problem of transmitting information by telegraph, concluded that an appropriate measure of the information in a message is the logarithm of the number of equivalent messages that might have been sent. For example, if a message consists of a sequence of n choices from k symbols, then the number of equivalent messages is 2n, and transmission of any one conveys an amount of information n log 2. In the hands of Wiener (3,4), Shannon (5). and others, Hartley's heuristic beginnings become a general, rigorous, elegant, and powerful theory related to statistical mechanics and promising to revolutionize communication theory. The ensemble of possible messages is characterized by a quantity completely analogous to entropy and called by that name, which measures the information conveyed by selection of one of the messages. In general, if a sub-ensemble is selected from a given ensemble, an amount of information equal to the difference of the entropies of the two ensembles is produced. A communication system is a means for transmitting information from a source to a destination and must be capable of transmitting any member of the ensemble from which the message is selected. Noise introduces uncertainty at the destination regarding the message actually sent. The difference between the a priori entropy of the ensemble of messages that might have been selected and the a posteriori entropy of the ensemble of messages that might have given rise to the received signal is reduced by noise so that less information is conveyed by the message.
It is clear that Hartley's definition of quantity of information agrees with Planck's definition of entropy if one correlates equivalent messages with independent wave functions. Wiener and Shannon generalize Hartley's definition to expressions of the same form as Boltzmann's definition (with the constant k suppressed) and call it entropy. It may seem confusing that a term connoting lack of information in physics is used as a measure of amount of information in communication, but the situation is easily clarified. If the message to be transmitted is known in advance to the recipient, no information is conveyed to him by it. There is no initial uncertainty or doubt to be resolved; the ensemble of a priori possibilities shrinks to a single case and hence has zero entropy. The greater the initial uncertainty, the greater the amount of information conveyed when a definite choice is made. In the physical case the message is not sent, so to speak, so that physical entropy measures how much physical information is missing. Planck's entropy measures how uncertain we are about what the actual wave function of the system is. Were we to determine it exactly, the system would have zero entropy (pure case), and our knowledge of the system would be maximal. The more information we lose, the greater the entropy, with statistical equilibrium corresponding to minimal information consistent with known energy and physical make-up of the system. We can thus equate physical information and negative entropy (or negentropy, a term proposed by Brillouin [9]). Szilard's result can be considered as giving thermodynamical support to the foregoing.
and S = k log P. MEASUREMENT AND COMMUNICATION
Let us now try to be more precise about what is meant by information in physics. Observation (measurement, experiment) is the only admissible means for obtaining valid information about the world. Measurement is a more quantitative variety of observation; e.g., we observe that a book is near the right side of a table, but we measure its position and orientation relative to two adjacent table edges. When we make a measurement, we use some kind of procedure and apparatus providing an ensemble of possible results. For measurement of length, for example, this ensemble of a priori possible results might consist of : (a) too small to measure, (b) an integer multiple of a smallest perceptible interval, (c) too large to measure. It is usually assumed that cases (a) and (c) have been excluded by selection of instruments having a suitable range (on the basis of preliminary observation or prior knowledge). One can define an entropy for this a priori ensemble, expressing how uncertain we are initially about what the outcome of the measurement will be. The measurement is made, but because of experimental errors there is a whole ensemble of values, each of which could have given rise to the one observed. An entropy can also be defined for this a posteriori ensemble, expressing how much uncertainty is still left unresolved after the measurement. We can define the quantity of physical information obtained from the measurement as the difference between initial (a priori) and final (a posteriori) entropies. We can speak of position entropy, angular entropy, etc., and note that we now have a quantitative measure of the information yield of an experiment. A given measuring procedure provides a set of alternatives. Interaction between the object of interest and the measuring apparatus results in selection of a subset thereof. When the results of this process of selection become known to the observer, the measurement has been completed.
It is now easy to see that there is an analogy between communication and measurement which actually amounts to an identity in logical structure.

PHYSICAL CONSEQUENCES OF THE INFORMATION
VIEWPOINT
Some implications of the informational viewpoint must be considered. First of all, the entropy of information theory is, except for a constant depending on choice of units, a straightforward generalization of the entropy concept of statistical mechanics. Information theory is abstract mathematics dealing with measurable sets, with choices from alternatives of an unspecified nature. Statistical mechanics deals with sets of alternatives provided by physics, be they wave functions, as Planck's quantal definition, or the complexions in phase space of classical quantum statistics. Distinguishing between identical particles (which leads to Gibbs' paradox and nonadditivity of entropy) is equivalent to claiming information that is not at hand, for there is no measurement yielding it. When this nonexistent information is discarded, the paradox vanishes. Symmetry numbers, accessibility conditions, and parity are additional items of (positive or negative) information entering into quantal entropy calculations.
Second, we can formulate the statistical expression of the second law of thermodynamics rather simply in terms of information : Our information about an isolated system can never increase (only by measurement can new information be obtained). Reversible processes conserve, irreversible ones lose information.
Third, all physical laws become relationships between types of information, or information functions collected or constructed according to various procedures. The difference between classical or quantum mechanics, on one hand, and classical or quantum statistics, on the other, is that the former is concerned with theoretically maximal information, the latter with less than the maximal. From the present viewpoint, therefore, classical and quantum mechanics are limiting cases of the corresponding statistics, rather than separate disciplines. The opposite limiting cases —namely, minimum information or maximum entropy —relate to the equilibrium distributions treated in texts on statistical mechanics. The vast, almost virgin field of nonequilibrium physics lies between these two extremes.
It is tempting to speculate that living matter is distinguished, at least in part, by having a large amount of information coded in its structure. This information would be in the form of "instructions" (constraints) restricting the manifold of possibilities for its physicochemical behavior. Perhaps instructions for developing an organism are "programmed" in the genes, just as the operation of a giant calculating machine, consisting of millions of parallel or consecutive operations, is programmed in a control unit. Schroedinger, in a fascinating little book, What Is Life? views living matter as characterized by its "disentropic" behavior, as maintaining its organization by feeding on "negative entropy," the thermodynamic price being a compensating increase in entropy of its waste products. Gene stability is viewed as a quantum effect, like the stability of atoms. In view of previous discussion, the reader should have no trouble fitting this into the informational picture above.
Returning to more prosaic things, we note, fourth, that progress either in theory of measurement or in theory of communication will help the other. Their logical equivalence permits immediate translation of results in one field to the other. Theory of errors and of noise, of resolving power and minimum detectable signal, of best channel utilization in communication and optimal experimental design are three examples of pairs where mutual cross-fertilization can be confidently expected.
Fifth, absolutely exact values of measured quantities are unattainable in general. For example, an infinite amount of information is required to specify a quantity capable of assuming a continuum of values. Only an ensemble of possibly "true" or "real" values is determined by measurement. In classical mechanics, where the state of a system is specified by giving simultaneous positions and momenta of all particles in the system, two assumptions are made at this point—namely, that the entropy of individual measurements can be made to approach zero, and furthermore that this can be done simultaneously for all quantities needed to determine the state of the system. In other words, the ensembles can he made arbitrarily sharp in principle, and these sharp values can be taken as "true" values. In current quantum mechanics the first assumption is retained, but the second is dropped. The ensembles of position and momenta values cannot be made sharp simultaneously by any measuring procedure. We are left with irreducible ensembles of possible "true" values of momentum, consistent with the position information on hand from previous measurements. It thus seems natural, if not unavoidable, to conclude that quantum mechanics describes the ensemble of systems consistent with the information specifying a state rather than a single system. The wave function is a kind of generating function for all the information deducible from operational specification of the mode of preparation of the system, and from it the probabilities of obtaining possible values of measurable quantities can be calculated. In communication terminology. the stochastic nature of the message source — i.e., the ensemble of possible messages and their probabilities — is specified, but not the individual message. The entropy of a given state for messages in x-language, p-language, or any other language, can he calculated in accordance with the usual rules. It vanishes in the language of a given observable if, and only if, the state is an eigenstate of that observable. For an eigenstate of an operator commuting with the Hamiltonian, all entropies are constant in time, analogous to equilibrium distributions in statistical mechanics. This results from the fact that change with time is expressed by a unitary transformation, leaving inner products in Hilbert space invariant. The corresponding classical case is one with maximal information where the entropy is zero and remains so. For a wave-packet representing the result of a position measurement, on the other hand, the distribution smears out more and more as time goes on, and its entropy of position increases. We conjecture, but have not proved, that this is a special case of a new kind of quantal H-theorem.
Sixth, the informational interpretation seems to resolve some well-known paradoxes (10). For example, if a system is in an eigenstate of some observable, and a measurement is made on an incompatible observable, the wave function changes instantaneously from the original eigenf unction to one of the second observable. Yet Schroedinger's equation demands that the wave function change continuously with time. In fact, the system of interest and the measuring equipment can be considered a single system that is unperturbed and thus varying continuously. This causal anomaly and action-at-a-distance paradox vanishes in the information picture. Continuous variation occurs so long as no new information is obtained incompatible with the old. New information results from measurement and requires a new representative ensemble. The system of interest could "really" change continuously even though our information about it did not. It does no harm to believe, as Einstein does, in a "real" state of an individual system, so long as one remembers that quantum mechanics does not permit an operational definition thereof. The Einstein-Podolsky-Rosen paradox (11), together with Schroedinger's (12) sharpening of it, seems to be similarly resolved. Here two systems interact for a short time and are then completely separated. Measurement of one system determines the state of the other. But the kind of measurement is under the control of the experimenter, who can, for example, choose either one of a pair of complementary observables. He obtains one of a pair of incompatible wave functions under conditions where an objective or "real" state of the system cannot be affected. If the wave function describes an individual system, one must renounce all belief in its objective or "real" state. If the wave function only bears information and describes ensembles consistent therewith, there is no paradox, for an individual system can be compatible with both of two inequivalent ensembles, as long as they have a nonempty intersection. The kind of information one gets simply varies with the kind of measurement one chooses to make.
REALITY, CAUSALITY, AND THE COMPLETENESS OF QUANTUM MECHANICS
We close with some general observations.
First, it is possible to believe in a "real" objective
state of a quantum-mechanical system without contradiction. As Bohr and Heisenberg have shown, states of simultaneous definite position and definite momentum in quantum mechanics are incompatible because they refer to simultaneous results of two mutually exclusive procedures. But, if a variable is not measured, its corresponding operation has not been I performed, and so unmeasured variables need not correspond to operators. Thus there need be no conflict with the quantum conditions. If one denies simultaneous reality to position and momentum then EPR forces the conclusion that one or the other assumes reality only when measured. In accepting this viewpoint, should one not assume, for consistency, that electrons in an atom have no reality, because any attempt to locate one by a photon will ionize the atom? The electron then becomes real (i.e., is "manufactured") only as a result of an attempt to measure its position. Similarly, one should also relinquish the continuum of space and time, for one can measure only a countable infinity of locations or instants, and even this is an idealization, whereas a continuum is uncountable. If one admits as simultaneously real all positions or times that might be measured, then for consistency simultaneous reality of position and momentum must be admitted, for either one might be measured.
Second, it is possible to believe in a strictly causal universe without contradiction. Quantum indeterminacy can be interpreted as reflecting the impossibility of getting enough information (by measurement) to permit prediction of unique values of all observables. A demon who can get physical information in other ways than by making measurements might then see a causal universe. Von Neumann's proof of the impossibility of making quantum mechanics causal by the introduction of hidden parameters assumes that these parameters are values that internal variables can take on, the variables themselves satisfying quantum conditions. Causality and reality (i.e., objectivity) have thus been rejected on similar grounds. Arguments for their rejection need not be considered conclusive for an individual system if quantum mechanics be viewed as a Gibbsian statistical mechanics of ensembles.
The third point is closely connected with this — namely, that quantum mechanics is both incomplete in Einstein's sense and complete in Bohr's sense (13). The former demands a place in the theory for the "real" or objective state of an individual system; the latter demands only that the theory correctly describe what will result from a specified operational procedure — i.e., an ensemble according to the present viewpoint. We believe there is no reason to exclude the possibility that a theory may exist which is complete in Einstein's sense and which would yield quantum mechanics in the form of logical inferences. In the communication analogy, Bohr's operational viewpoint corresponds to demanding that the ensemble of possible messages be correctly described by theory when the procedure determining the message source is given with maximum detail. This corresponds to the attitude the telephone engineer who is concerned with trans- itting the human voice but who is indifferent to the eaning of the messages. Einstein's attitude implies at the messages may have meaning, the particular eaning to be conveyed determining what message is selected. Just as no amount of telephonic circuitry can engender semantics, so does "reality" seem beyond experiment as we know it. It seems arbitrary, however, to conclude that the problem of reality is meaningless or forever irrelevant to science. It is conceivable, for example, that a long sequence of alternating measurements on two noncommuting variables carried out on a single system might suggest new kinds of regularity. These would, of course, have to yield the expectation values of quantum mechanics.
References
1. SZILARD, L. Z. Physik, 53, 840 (1929).2. HARTLEY, R. V. L. Bell System Tech. J., 27, 535 (1928). 3. WIENER, N. Cybernetics. New York : Wiley (1950). 4.______ The Extrapolation, Interpolation and Smoothing of Time Series. New York : Wiley (1950). 5. SHANNON, C. E. Bell System Tech. J., 27, 279, 623 (1948): Proc. I. R. E., 37, 10 (1949). 6. TULLER, W. G. Proc. I. R. E., 37, 468 (1949). 7. GABOR, D. J. Inst. Elec. Engrs. (London), Pt. III, 93, 429 (1946) ; Phil. Mag., 41, 1161 (1950). 8. MACKAY, D. M. Phil. Mag., 41, 289 (1950). 9. BRILLOUIN, L. J. Applied Phys., 22, 334, 338 (1951). 10. REICHENBACH, H. Philosophical Foundations of Quantum Mechanics. Berkeley : Univ. Calif. Press (1944). 11. EINSTEIN, A., PODOLSKY, B., and ROSEN, N. Phys. Rev., 47, 777 (1935). 12. SCHROEDINGER, E. Proc. Cambridge Phil. Soc., 31, 555 (1935) ; 32, 466 (1936). 13. BOHR, N. Phys. Rev., 48, 696 (1935). For Teachers
For Scholars
|