Leucippus (440 B.C.E.) stated the first dogma of determinism, an absolute necessity.

Nothing occurs by chance (maton), but there is a reason (logos) and necessity (ananke) for everything.

Chance is regarded as inconsistent with causal determinism and with physical or mechanical determinism.

The idea that Chance and Necessity are the only two logical options, and that neither is compatible with free will and moral responsibility, is the basis for the standard argument against free will.

The first thinker to suggest a physical explanation for chance in the universe was Epicurus. Epicurus was influenced strongly by Aristotle, who regarded chance as a fifth cause. Epicurus said there must be cases in which the normally straight paths of atoms in the universe occasionally bend a little and the atoms "swerve" to prevent the universe and ourselves from being completely determined by the mechanical laws of Democritus.

For Epicurus, the chance in his atomic swerve was simply a means to deny the fatalistic future implied by determinism (and necessity). As the Epicurean Roman Lucretius explained the idea,

...if all motion is always one long chain, and new motion arises out of the old in order invariable, and if the first-beginnings do not make by swerving a beginning of motion such as to break the decrees of fate, that cause may not follow cause from infinity, whence comes this freedom in living creatures all over the earth
(De Rerum Natura, Book 2, lines 251-256)

Epicurus did not say the swerve was directly involved in decisions so as to make them random. His critics, ancient and modern, have claimed mistakenly that Epicurus did assume "one swerve - one decision." Some recent philosophers call this the "traditional interpretation" of Epicurean free will.

On the contrary, following Aristotle, Epicurus thought human agents have an autonomous ability to transcend the necessity and chance of some events. He said that this special ability makes us morally responsible for our actions.

Epicurus, clearly following Aristotle, finds a tertium quid, beyond necessity (Democritus' physics) and chance
(Epicurus' swerve).
The tertium quid is agent autonomy

...some things happen of necessity (ἀνάγκη), others by chance (τύχη), others through our own agency (παρ’ ἡμᾶς).
...necessity destroys responsibility and chance is uncertain; whereas our own actions are autonomous, and it is to them that praise and blame naturally attach.

λέγει ἐν ἄλλοις γίνεσθαι ἃ μὲν κατ’ ἀνάγκην, ἃ δὲ ἀπὸ τύχης, ἃ δὲ παρ’ ἡμᾶς, διὰ τὸ τὴν μὲν ἀνάγκην ἀνυπεύθυνον εἶναι, τὴν δὲ τύχην ἄστατον ὁρᾶν, τὸ δὲ παρ’ ἡμᾶς ἀδέσποτον, ᾧ καὶ τὸ μεμπτὸν καὶ τὸ ἐναντίον παρακολουθεῖν πέφυκεν
(Letter to Menoeceus, §133)

Despite abundant evidence, many philosophers deny that real chance exists. If a single event is determined by chance, then indeterminism would be true, they say, and undermine the very possibility of certain knowledge. Some go to the extreme of saying that chance makes the state of the world totally independent of any earlier states, which is nonsense, but it shows how anxious they are about chance.

The Stoic Chrysippus (200 B.C.E.) said that a single uncaused cause could destroy the universe (cosmos), a concern shared by some modern philosophers, for whom reason itself would fail.

Everything that happens is followed by something else which depends on it by causal necessity. Likewise, everything that happens is preceded by something with which it is causally connected. For nothing exists or has come into being in the cosmos without a cause. The universe will be disrupted and disintegrate into pieces and cease to be a unity functioning as a single system, if any uncaused movement is introduced into it.

A major achievement of the Ages of Reason and Enlightenment was to banish absolute chance as unintelligible and atheistic. In the seventeenth century, Newton's Laws provided a powerful example of deterministic laws governing the motions of everything. Surely Leucippus' and Democritus' original insights into materialistic determinism had been confirmed by Newton.

In 1718, Abraham De Moivre wrote a book called The Doctrine of Chances. It was very popular among gamblers. In the second edition (1738), he derived the mathematical form of the normal distribution of probabilities, but he denied the reality of chance. Because it implied events that God could not know, he labeled it atheistic.

Chance, in atheistical writings or discourse, is a sound utterly insignificant: It imports no determination to any mode of existence; nor indeed to existence itself, more than to non existence; it can neither be defined nor understood.

De Moivre's book (in three editions between 1718 and 1756) was basically a handbook for gamblers. It enabled them to know how to bet in various games of chance.

It begins...

The Probability of an Event is greater or less, according to the number of Chances by which it may happen, compared with the whole number of Chances by which it may happen or fail.

This brief statement contains the assumption that all states are equally probable, assuming that we have no information that indicates otherwise.

While this describes our information epistemically, making it a matter of human knowledge, we can say ontologically that the world contains no information that would make any state more probable than the others. Such information simply does not exist. This is sometimes called the principle of insufficient reason or the principle of indifference.

If that information did exist, it could and would be revealed in large numbers of experimental trials, which provide the statistics on the different "states."

Probabilities are a priori theories.
Statistics are a posteriori, the results of experiments.

In the philosophical controversies between a priori or epistemic (e.g., "propensity") interpretations of probability and a posteriori or ontological interpretations, the latter are often said to be "frequency" interpretations of probability. We prefer to use the term statistics.

The frequencies of outcomes in experimental statistics confirm the correctness of probability theories based on the number of different ways independent and equiprobable events can combine, e.g, the number of white balls versus black balls in an urn, or the number of ways cards can combine to provide a royal straight flush.

The complex coefficients of different quantum states (vectors) in the expansion of an arbitrary state in terms of basis states, when squared, give us the probabilities of finding a system in one of those otherwise equally probable basis states.

De Moivre discovered the normal distribution (the bell curve) of outcomes for ideal random processes, like the throw of dice. Perfectly random processes produce a regular distribution pattern for many trials. The law of large numbers in probability theory ensures that the agreement between theoretical probabilities and experimental statistics approaches perfection as the number of trials approaches infinity.

Paradoxically, the discovery of regularities in various social phenomena led many mathematicians to conclude that the phenomena are determined, perhaps by unknown laws. They do not believe events are ontologically random. Most all the mathematicians of probability have denied the existence of real chance in the world.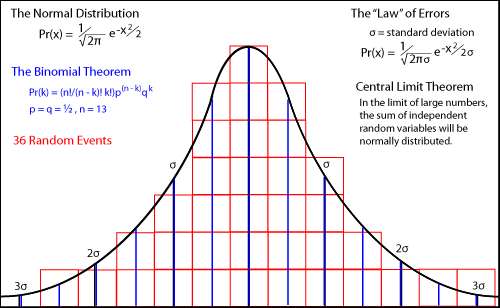

As early as 1784, the great Immanuel Kant argued in his Idea for a Universal History with a Cosmopolitan Intent that the regularities in social events from year to year show that they must be determined.

No matter what conception may form of the freedom of the will in metaphysics, the phenomenal appearances of the will, i.e., human actions, are determined by general laws of nature like any other event of nature. History is concerned with telling about these events. History allows one to hope that when history considers in the large the play of the freedom of human will, it will be possible to discover the regular progressions thereof. Thus (it is to be hoped) that what appears to be complicated and accidental in individuals, may yet be understood as a steady, progressive, though slow, evolution of the original endowments of the entire species. Thus, given that the free will of humans has such a great influence on marriages, on the births that result from these, and on dying, it would seem that there is no rule to which these events are subject and according to which one could calculate their number in advance. And yet the relevant statistics compiled annually in large countries demonstrate that these events occur just as much in accordance with constant natural laws as do inconstancies in the weather, which cannot be determined individually in advance, but which, taken together, do not fail to maintain a consistent and uninterrupted process in the growth of the plants, the flow of the rivers, and other natural arrangements.

(Kant, Idea for a Universal History, 1784)

Following de Moivre, mathematical theorists of games of chance found ways to argue that the chance they described was somehow necessary and that chance outcomes were actually determined. The most famous of these, Pierre-Simon Laplace, preferred to call his theory the "calculus of probabilities." With its connotation of approbation, probability is a more respectable term than chance, which had dark associations with gambling and lawlessness. For Laplace, random outcomes are not predictable only because we lack the detailed information to predict. As did the ancient Stoics, Laplace explained the appearance of chance as the result of human ignorance. It is epistemic, in modern terms. Laplace said,

"The word 'chance,' then expresses only our ignorance of the causes of the phenomena that we observe to occur and to succeed one another in no apparent order."

Laplace's several works on probability (Théorie des probabilités , Théorie analytique des probabilités , and Essai philosophique sur les probabilités) establish many of the techniques and results of modern probability and statistics, including the method of least squares for assessing observational data. His "central limit theorem" of 1811 was a mathematical expression for how the law of large numbers reduces the dispersion around mean values. Perhaps most importantly, Laplace defended the idea of a priori probabilities that can be used to reason about future events.

In the introduction to the Essai, he extended an idea of Gottfried Leibniz which became famous as Laplace's Demon, a key vision of strict physical determinism. He said

"We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes."

In the 1820's, perhaps following Kant, Adolphe Quetelet and Henry Thomas Buckle argued that regularities in social behavior prove that individual acts like marriage and suicide are determined by natural law.

Adolphe Quételet was a Belgian astronomer, mathematician, and sociologist. He interpreted the "statistical" information being gathered by modern states, especially the voluminous statistical data collected in Paris by the great French mathematician Joseph Fourier, as evidence that some phenomena like marriages and suicides were somehow being determined by an unknown law. Fourier noticed that statistics on the number of births, deaths, marriages, suicides, and various crimes in the city of Paris had remarkably stable averages from year to year.

Individuals might think marriage was their decision, but since the number of total marriages was relatively stable from year to year, Quételet claimed the individuals were determined to marry. Quételet used Auguste Comte's term "social physics, to describe his discovery of "laws of human nature." This forced Comte to rename his own work "sociologie."

Quételet's argument for determinism in human events is quite illogical. It appears to go something like this:

• Perfectly random, unpredictable individual events (like the throw of dice in games of chance) show statistical regularities that become more and more certain with more trials (the law of large numbers).
• Human events show statistical regularities.
• Therefore, human events are determined.

Quételet might more reasonably have concluded that individual human events are unpredictable and random. Were they determined, they might be expected to show a non-random pattern, perhaps a signature of the Determiner.

Buckle made a great contribution to the discussion of Free Will in the long Introduction to his three-volume History of Civilization in England in 1872. His work had fully digested the implications of Immanuel Kant's Critiques, which put human freedom in a realm beyond observation and ordinary understanding. Buckle's work should perhaps be seen as following the prescription of Kant in his Idea for a Universal History with a Cosmopolitan Intent.
Buckle mistakenly concluded that

In regard to nature, events apparently the most irregular and capricious have been explained, and have been shown to be in accordance with certain fixed and universal laws. This has been done because, men of ability, and, above all, men of patient, untiring thought, have studied natural events with the view of discovering their regularity: and if human events were subjected to a similar treatment, we have every right to expect similar results.

(History of Civilization in England, Introduction, 1856)

When he published his epochal Origin of Species in 1859, Charles Darwin had just a few words about the role of chance as the source of the genetic variations needed for his theory of natural selection. His use of the word "chance" is overwhelmingly to describe the chances of acquiring new characters and the chances of survival, and only rarely to the role of chance in the genetic variations that drive natural selection. He is reluctant to describe the details of genetic variation, perhaps because ascribing it simply to chance is scientifically unsatisfying. When he does come to connect chance to variation, he takes chance to be the result of human ignorance, leaving the door open to a better explanation in the future?

I HAVE hitherto sometimes spoken as if the variations so common and multiform in organic beings under domestication, and in a lesser degree in those in a state of nature had been due to chance. This, of course, is a wholly incorrect expression, but it serves to acknowledge plainly our ignorance of the cause of each particular variation. Some authors believe it to be as much the function of the reproductive system to produce individual differences, or very slight deviations of structure, as to make the child like its parents. But the much greater variability, as well as the greater frequency of monstrosities, under domestication or cultivation, than under nature, leads me to believe that deviations of structure are in some way due to the nature of the conditions of life, to which the parents and their more remote ancestors have been exposed during several generations.
(The Origin of Species, chapter V, Laws of Variation.)

But Darwin's Notebooks, especially his "transmutation notebooks," and the later M and N metaphysical notebooks, record some of Darwin's brief musings on the connection between "free will" and chance.

In his Notebooks on Man, Mind and Materialism, Darwin says...

Now it is not a little remarkable that the fixed laws of nature should be ^{/universally/} thought to be the will of a superior being, whose nature can only be rudely traced out. When one sees this, one suspects that our will may ^{/arise from/} fixed laws of organization. M. le Comte argues against all contrivance — it is what my views tend to.

Darwin thinks the fixed laws of nature are enough to explain the world in materialistic terms. No superior contriving being is required. Darwin connects free will with chance, but it is epistemic chance. It produces random new possibilities, but they are completely determined by natural laws.

the free will (if so called) makes change in bodily organization of oyster, so may free will make change in man. — the real argument fixes on hereditary disposition & instincts. — Put it so. — Probably some error in argument, should be grateful if it were pointed out. My wish to improve my temper, what does it arise from, but organization, that organization may have been affected by circumstances & education & by the choice which at that time organization gave me to will — Verily the faults of the fathers, corporeal & bodily, are visited upon the children.—

Darwin sees a multiplicity of causes - hereditary, education, circumstances - that appear random and may not be known exactly. They show up as new organization (information structures?) in the individual.

The above views would make a man a predestinarian of a new kind, because he would tend to be an atheist... It may be doubted whether a man intentionally can wag his finger from real caprice. it is chance which way it will be, but yet it is settled by reason.

Darwin's new kind of predestination is purely material - the result of physical laws - and not the "contrivances" or "designs" of a deity. He appears to combine chance and reason in a two-stage view - "chance it will be, yet settled by reason" - that sounds like evolution?

what they teach by the same means & therefore properly no free will. — we may easily fancy there is, as we fancy there is such a thing as chance. — chance governs the descent of a farthing, free will determines our throwing it up, — equally true the two statements...

I verily believe free will & chance are synonymous. — Shake ten thousand grains of sand together & one will be uppermost, — so in thoughts, one will rise according to law.

Darwin drew a bracket of emphasis alongside the sentence above in his notebook. The preliminary random shaking stage, followed by a lawful rise, strongly suggests a combination of indeterministic chance and some level of determinism as in the Cogito two-stage model. The etymology of cogito is to shake together (co-agitare).

The work of Quételet and Buckle on social statistics, and their mathematical expression in the form of a "bell curve" or "normal" distribution (also called Gaussian), may have led James Clerk Maxwell to derive his famous distribution of molecule velocities in a gas that has reached thermal equilibrium. But in 1860 Maxwell found a significant departure from the symmetric Gaussian in the distribution of molecular velocities.

Where "normal" errors are distributed symmetrically around the mean value, falling away from the mean as e ^{- x2} , the Maxwell-Boltzmann distribution of velocities increases as v² for low velocity particles. It reaches a peak value, then declines according to the Gaussian exponential e ^{- v2} for high velocities.

Maxwell's criticism of his countryman Buckle was clear.

We thus meet with a new kind of regularity — the regularity of averages — a regularity which when we are dealing with millions of millions of individuals is so unvarying that we are almost in danger of confounding it with absolute uniformity.

Maxwell comes close to asserting ontological chance, but he may only be saying one cannot derive determinism from statistical regularities

Laplace in his theory of Probability has given many examples of this kind of statistical regularity and has shown how this regularity is consistent with the utmost irregularity among the individual instances which are enumerated in making up the results. In the hands of Mr Buckle facts of the same kind were brought forward as instances of the unalterable character of natural laws. But the stability of the averages of large numbers of variable events must be carefully distinguished from that absolute uniformity of sequence according to which we suppose that every individual event is determined by its antecedents.²

(Draft Lecture on Molecules, 1784)

In 1866, Ludwig Boltzmann rederived Maxwell's velocity distribution of gas particles. He did it assuming that the physical motion of each particle (or atom) was determined exactly by Newton's laws. And in 1872, when he first showed how his kinetic theory of gases could explain the increase in entropy, Boltzmann again used strictly deterministic physics. But his former teacher Josef Loschmidt objected to Boltzmann's derivation of the second law. Loschmidt said that if time were reversed, the deterministic laws of classical mechanics would require that the entropy would go down, not up.

So in 1877 Boltzmann reformulated his H-Theorem, his proof of entropy increase. assuming that each collision of gas particles was not determined, but random. He assumed that the directions and velocities of particles after a collision depended on chance, as long as energy and momentum were conserved. He could then argue that the particles would be distributed randomly in "phase space" based on the statistical assumption that individual cells of phase space were equally probable. His H-Theorem produced a quantity which (statistically) would go only up, independent of the time direction.

Where Maxwell had used math from social statistics, Boltzmann declared that the fundamental interactions of microscopic particles was in fact statistical. Much later he came to call it "molecular disorder." A law of nature, the second law of thermodynamics, had become statistical. Did Boltzmann believe that ontological chance existed? Or was this just the use of probability because the number of variables is too great to know the microscopic details?

Boltzmann explained that probabilities can give definite macroscopic results because of the large number of particles in a gas, but that the use of probabilities and lack of microscopic predictability does not imply significant macroscopic uncertainty in the theory of heat.

The mechanical theory of heat assumes that the molecules of a gas are not at rest, but rather are in the liveliest motion. Hence, even though the body does not change its state, its individual molecules are always changing their states of motion, and the various molecules take up many different positions with respect to each other. The fact that we nevertheless observe completely definite laws of behaviour of warm bodies is to be attributed to the circumstance that the most random events, when they occur in the same proportions, give the same average value. For the molecules of the body are indeed so numerous, and their motion is so rapid, that we can perceive nothing more than average values.

Boltzmann refers to the social statistics of Adolphe Quételet and Henry Thomas Buckle

One might compare the regularity of these average values with the amazing constancy of the average numbers provided by statistics, which are also derived from processes each of which is determined by a completely unpredictable interaction with many other factors. The molecules are likewise just so many individuals having the most varied states of motion, and it is only because the number of them that have, on the average, a particular state of motion is constant, that the properties of the gas remain unchanged. The determination of average values is the task of probability theory. Hence, the problems of the mechanical theory of heat are also problems of probability theory.

In the 1870's, Boltzmann clearly sees probability as a deterministic theory.

It would, however, be erroneous to believe that the mechanical theory of heat is therefore afflicted with some uncertainty because the principles of probability theory are used. One must not confuse an incompletely known law, whose validity is therefore in doubt, with a completely known law of the calculus of probabilities; the latter, like the result of any other calculus, is a necessary consequence of definite premises, and is confirmed, insofar as these are correct, by experiment, provided sufficiently many observations have been made, which is always the case in the mechanical theory of heat because of the enormous number of molecules involved.

("Further Studies on the Thermal Equilibrium of Gas Molecules," Vienna Academy of Sciences, 1872)

One of Boltzmann's students, Franz S. Exner, defended the idea of absolute chance and indeterminism as a hypothesis that could not be ruled out on the basis of observational evidence. Exner did this in his 1908 inaugural lecture at Vienna University as rector (two years after Boltzmann's death), and ten years later in a book written during World War I. But Exner's view was not the standard view. Ever since the eighteenth-century development of the calculus of probabilities, scientists and philosophers assumed that probabilities and statistical phenomena, including social statistics, were completely determined. They thought that our inability to predict individual events was due simply to our ignorance of the details.

In his 1922 inaugural address at the University of Zurich, What Is a Law of Nature?, Erwin Schrödinger said about Exner, who had been his teacher,

"It was the experimental physicist, Franz Exner, who for the first time, in 1919, launched a very acute philosophical criticism against the taken-for-granted manner in which the absolute determinism of molecular processes was accepted by everybody. He came to the conclusion that the assertion of determinism was certainly possible, yet by no means necessary, and when more closely examined not at all very probable.

"Exner's assertion amounts to this: It is quite possible that Nature's laws are of thoroughly statistical character. The demand for an absolute law in the background of the statistical law — a demand which at the present day almost everybody considers imperative — goes beyond the reach of experience."

Ironically, just four years later, after developing his continuous and deterministic wave theory of quantum mechanics, Schrödinger would himself "go beyond the reach of experience" searching for deterministic laws underlying the discontinuous, discrete, statistical and probabilistic indeterminism of the Bohr-Heisenberg school, to avoid the implications of absolute chance in quantum mechanics. Max Planck and Albert Einstein too were repulsed by randomness and chance. "God does not play dice," was Einstein's famous remark. But we shall show that in 1916 Einstein was the first person to see the ontological chance that is fundamental to quantum theory.

Franz Exner was not alone in defending chance before quantum uncertainty. In the nineteenth century in America, Charles Sanders Peirce coined the term "tychism" for his idea that absolute chance was the first step in three steps to "synechism" or continuity.

Peirce was influenced by the social statisticians Buckle and Quetelet, and by French philosophers Charles Renouvier and Alfred Fouillee, who also argued for some absolute chance, by physicists Maxwell and Boltzmann, but most importantly by Kant and Hegel, who saw things arranged in the triads that Peirce so loved.

Renouvier and Fouillee introduced chance or indeterminism simply to contrast it with determinism, and to discover some way, usually a dialectical argument like that of Hegel, to reconcile opposites. Renouvier argues for human freedom, but nowhere explains exactly how chance might contribute to that freedom, other than negating determinism.

Peirce does not explain much with his Tychism, and with his view that continuity and evolutionary love is supreme, may have had doubts about the importance of chance. Peirce did not propose chance as directly or indirectly providing free will. He never mentions the ancient criticisms that we cannot accept responsibility for chance decisions. He does not really care for chance as the origin of species, preferring a more deterministic and continuous lawful development, under the guidance of evolutionary love. But Peirce does say clearly, well before Exner, that the observational evidence simply does not establish determinism.

It remained for William James, Peirce's close friend, to assert that chance can provide random unpredictable alternative possibilities from which the will can choose or determine one alternative. James was the first thinker to enunciate clearly a two-stage decision process, with chance in a present time of random alternatives, leading to a choice which selects one alternative and transforms an equivocal ambiguous future into an unalterable determined past. There are undetermined alternatives followed by adequately determined choices.

"The stronghold of the determinist argument is the antipathy to the idea of chance...This notion of alternative possibility, this admission that any one of several things may come to pass is, after all, only a roundabout name for chance...

What is meant by saying that my choice of which way to walk home after the lecture is ambiguous and matter of chance?...It means that both Divinity Avenue and Oxford Street are called but only one, and that one either one, shall be chosen." (James, The Dilemma of Determinism, in The Will to Believe, 1897, p.155)

Chance is critically important for the question of free will because strict necessity implies just one possible future. Absolute chance means that the future is fundamentally unpredictable at the levels where chance is dominant. Chance allows alternative futures and the question becomes how the one actual present is realized from these potential alternative futures.

The amount of chance and the departure from strict causality required for free will is very slight compared to the miraculous ideas often associated with the "causa sui" (self-caused cause) of the ancients. For medieval philosophers, only God could produce a causa sui, a miracle. Modern quantal randomness, unless amplified to the macroscopic world, is generally insignificant, not a miracle at all.

Despite David Hume's critical attack on causality, many philosophers embrace causality strongly, including Hume himself in his other writings, where he dogmatically asserts "'tis impossible to admit of any medium betwixt chance and an absolute necessity." Since Chrysippus twenty-two centuries ago, philosophers still connect causality to the very possibility of logic and reason.

Bertrand Russell wrote in 1914:

"The law of causation, according to which later events can theoretically be predicted by means of earlier events, has often been held to be a priori, a necessity of thought, a category without which science would not be possible."

(Our Knowledge of the External World, 1914, p.179)

Although he felt some claims for causality might be excessive, Russell was unwilling to give up strict determinism, saying "Where determinism fails, science fails," and "What science cannot discover, mankind cannot know." (Determinism and Physics, p.18)

Also in 1914, the great polymath Henri Poincaré wrote

"How can we venture to speak of the laws of chance? Is not chance the antithesis of all law?" It is thus that Bertrand expresses himself at the beginning of his "Calculus of Probabilities." Probability is the opposite of certainty; it is thus what we are ignorant of, and consequently it would seem to be what we cannot calculate. There is here at least an apparent contradiction, and one on which much has already been written

To begin with, what is chance? The ancients distinguished between the phenomena which seemed to obey harmonious laws, established once for all, and those that they attributed to chance, which were those that could not be predicted because they were not subject to any law. In each domain the precise laws did not decide everything, they only marked the limits within which chance was allowed to move. In this conception, the word chance had a precise, objective meaning ; what was chance for one was also chance for the other and even for the gods.

But this conception is not ours. We have become complete determinists, and even those who wish to reserve the right of human free will at least allow determinism to reign undisputed in the inorganic world. Every phenomenon, however trifling it be, has a cause, and a mind infinitely powerful and infinitely well-informed concerning the laws of nature could have foreseen it from the beginning of the ages. If a being with such a mind existed, we could play no game of chance with him, we should always lose.

For him, in fact, the word chance would have no meaning, or rather there would be no such thing as chance. That there is for us is only on account of our frailty and our ignorance. And even without going beyond our frail humanity, what is chance for the ignorant is no longer chance for the learned. Chance is only the measure of our ignorance. Fortuitous phenomena are, by definition, those whose laws we are ignorant of...

(Science and Method, chapter 4, Chance, 1914, p.64)

It is certain that the combinations which present themselves to the mind in a kind of sudden illumination after a somewhat prolonged period of unconscious work are generally useful and fruitful combinations, which appear to be the result of a preliminary sifting. Does it follow from this that the subliminal ego, having divined by a delicate intuition that these combinations could be useful, has formed none but these, or has it formed a great many others which were devoid of interest, and remained unconscious?

Under this second aspect, all the combinations are formed as a result of the automatic action of the subliminal ego, but those only which are interesting find their way into the field of consciousness. This, too, is most mysterious.

Poincaré knows that chance can not be the direct cause of our actions

How can we explain the fact that, of the thousand products of our unconscious activity, some are invited to cross the threshold, while others remain outside? Is it mere chance that gives them this privilege? Evidently not...

What follows, then? Of the very large number of combinations which the subliminal ego blindly forms almost all are without interest and without utility. But, for that very reason, they are without action on the aesthetic sensibility; the consciousness will never know them.

Focusing attention, as James pointed out, can make an adequately determined selection from random alternative possibilities which come to consciousness

A few only are harmonious, and consequently at once useful and beautiful, and they will be capable of affecting the geometrician's special sensibility I have been speaking of; which, once aroused, will direct our attention upon them, and will thus give them the opportunity of becoming conscious...

In the subliminal ego, on the contrary, there reigns what I would call liberty, if one could give this name to the mere absence of discipline and to disorder born of chance. Only, this very disorder permits of unexpected couplings.

(Science and Method, chapter 4, Mathematical Discovery, 1914, p.58)

Planck's radical assumption quickly led to the quantum theory we have today. Just five years after Planck, Albert Einstein took Planck's idea and found that light quanta - discrete discontinuous particles - must exist even as continuous light waves also exist. This would lead Einstein to show that ontological chance exists in the universe, a consequence he could never accept because of his deep beliefs in natural laws, as we shall see.

Planck said:

"Just as no physicist will in the last resort acknowledge the play of chance in human nature, so no physiologist will admit the play of chance in the absolute sense."

"the assumption of chance in inorganic nature is incompatible with the working principle of natural science."

(Where Is Science Going,p.147, p.154.)

We know that even in a world with microscopic chance, macroscopic objects are adequately determined to an extraordinary degree. Newton's laws of motion are deterministic enough to send men to the moon and back. In our Cogito model, the Macro Mind is macroscopic enough to ignore quantum uncertainty for the purpose of the reasoning will. The neural system is robust enough to insure that mental decisions are reliably transmitted to our limbs.

We call this kind of determinism "adequate determinism." Despite quantum uncertainty, the world is adequately determined to send men to the moon. Quantum uncertainty leads some philosophers to fear an undetermined world of chance, one where Chrysippus' imagined collapse into chaos would occur and reason itself would fail us. But the modest indeterminism required for free will is no chaotic irrational threat, since most physical and mental events are overwhelmingly "adequately determined," determined "for all practical purposes."

There is no problem imagining that the three traditional mental faculties of reason - perception, conception, and comprehension - are all carried on with "adequate determinism" in a physical brain where quantum events and thermal noise do not interfere with normal operations.

There is also no problem imagining a role for chance in the brain in the form of quantum level noise (as well as pre-quantal thermal noise). Noise can introduce random errors into stored memories. Noise could create random associations of ideas during memory recall. Many scientists have speculated that this randomness may be driven by microscopic fluctuations that are amplified to the macroscopic level. This would not happen in some specific location in the brain. It is most likely a general property of all neurons.

We distinguish seven increasingly sophisticated ideas about the role of chance and indeterminism in the question of free will. Many libertarians have accepted the first two. Determinist and compatibilist critics of free will make the third their central attack on chance, claiming that it denies moral responsibility. But very few thinkers appear to have considered all seven essential requirements for chance to contribute to libertarian free will.

1. Chance exists in the universe. Quantum mechanics is correct. Indeterminism is true, etc.

2. Chance is important for free will because it breaks the causal chain of determinism.

3. But chance cannot directly cause our actions. We cannot be responsible for random actions.

4. Chance can only generate random (unpredictable) alternative possibilities for action or thought. The choice or selection of one action must be adequately determined, so that we can take responsibility. And once we choose, the connection between mind/brain and motor control must be adequately determined to see that "our will be done."

5. Chance, in the form of noise, both quantum and thermal noise, must always be present. The naive model of a single random microscopic event, amplified to affect the macroscopic brain, never made sense. Under what ad hoc circumstances, at what time, at what place in the brain, would it occur to affect a decision?

6. Chance must be overcome or suppressed by the adequately determined will when it decides to act, de-liberating the prior free options that "one could have done."

7. To the extent that chance is not completely suppressed by the will, the resulting choice can be considered to have an element of randomness. The agent can still take responsibility for allowing the choice to be partially or completely random, the equivalent of flipping a mental coin.