Putnam, famous for his various theories about "realism," claims that future events are already "real." This is a "tenseless" view of the future, like that of J. J. C. Smart's block universe of special relativity.

Putnam discusses the related problems of the truth of "future contingents" and Aristotle's famous "sea-battle." Also see Diodorus Cronus's Master Argument.

Putnam's argument depends on paradoxes (the most famous being the twin paradox) that are the results of moving observers having different ideas about what events in their view correspond to "now." They have different "planes of simultaneity." "Now" means they have synchronized their clocks according to Einstein's famous procedure.

A moving observer B thinks some event in his plane of simultaneous events is in B's future. At the same (cosmic time) moment, an observer A thinks that B is in his (A's) plane of simultaneity.

But this is not a transitive relation. Just because A sees B as his "now" and B sees an event in A's future as B's "now" does not make the event in A's future "now" for A.

Putnam says

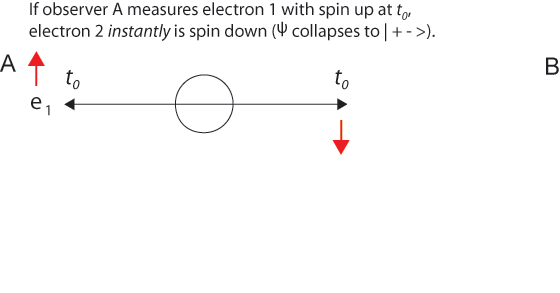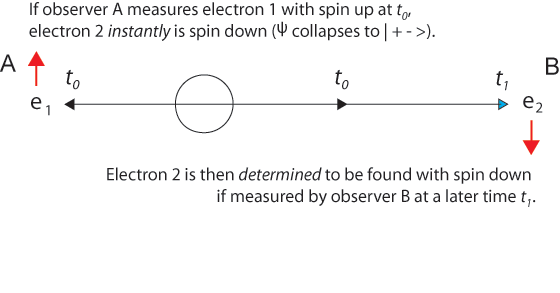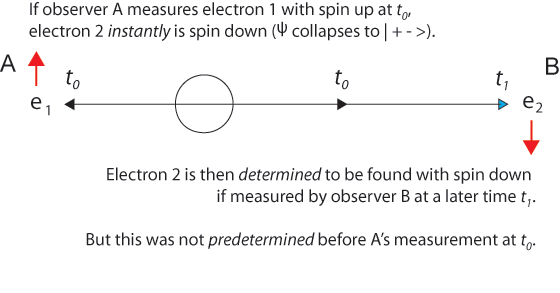
(1) All (and only) things that exist now are real.

Future things (which do not already exist) are not real (on this view); although, of course they will be real when the appropriate time has come to be the present time. Similarly, past things (which have ceased to exist) are not real, although they were real in the past.

If we assume classical physics and take the relation R to be the relation of simultaneity, then, on the view (1), it is true that all and only the things that stand in the relation R to me-now are real.

We now discover something really remarkable. Namely, on every natural choice of the relation R, it turns out that future things (or events) are already real!"

you-now and I-now are at the same place now, but moving with relative velocities which are very large (relative to the speed of light, which I take to be = 1). Thus, our world-lines look as shown in figure 1 (I have also drawn our "lightcone" for the purpose of the later discussion):

It is well known that, as a consequence of Special Relativity, there are events which lie in "the future" according to my coordinate system and which lie in the "present" of you-now according to your coordinate system. Since these things stand in the relation R to you-now, and you-now are real, and it was assumed that all and only the things that stand in the relation R to me-now are real, the principle III requires that I call these future things and events real! (But, actually, I now have a contradiction: for these future things do not stand in the relation R to me-now, and so my assumption that all and only the things that stand in this relation R to me-now are real was already inconsistent with the principle that There Are No Privileged Observers.)

The difficulty is obvious: what the principle that There Are No Privileged Observers requires is simply that the relation R be transitive; i.e., that it have the property that from xRy and yRz it follow that xRz. Simultaneity-in-my-coordinate-system has this property, since if x is simultaneous with y in my coordinate system, and y is simultaneous with z in my coordinate system, then x is also simultaneous with z in my coordinate system; but simultaneity-in-my-coordinate system is not admissible as a choice of R, because it depends on the coordinate system. And the relation "x is simultaneous with y in the coordinate system of x" (which is essentially the relation we just considered), while admissible, is not transitive, since, if I-now am simultaneous with you-now in the coordinate system of me-now, and you-now are simultaneous with event X in the coordinate system of you-now, it does not follow that I-now am simultaneous with event X in the coordinate system of me-now.

Now then, if we combine the fact that the relation R is required by iii to be transitive with our desire to preserve the following principle, which is one-half of (1):

(2) All things that exist now are real.

-then we quickly see that future things must be real.

For, if the relation R satisfies (2)-and I take (2) to mean (at least when I assert it) that all things that exist now according to my coordinate system are real-and you-now are as in figure 1, then you-now must stand in the relation R to me-now, since you exist both now and here. But, if the relation R always holds between all the events that are on some one "simultaneity line" in my coordinate system and meat- the-appropriate-time, then (since the laws of nature are invariant under Lorentz transformation, by the principle of Special Relativity), the relation R must also hold between all the events on some one "simultaneity-line" in any observer's coordinate system and that-observer- at-the-appropriate-time. Hence, all the events that are simultaneous with you-now in your coordinate system must also bear the relation R to you-now. Let event X be one such event which is "in the future" according to my coordinate system (if our velocities are as shown in figure 1, then such an event X must always exist). Then, since the event X bears the relation R to you-now, and you-now bear the relation R to me-now, the event X bears the relation R to me-now. But we chose R to be such that all and only those events which bear R to me-now are real. So the event X, which is a future event according to my coordinate system, is already real!

I conclude that the problem of the reality and the determinateness of future events is now solved. Moreover, it is solved by physics and not by philosophy. We have learned that we live in a four-dimensional and not a three-dimensional world, and that space and time or, better, space-like separations and time-like separations - are just two aspects of a single four-dimensional continuum with a peculiar metric which sometimes permits distance (y, x) = 0 even when x ≠ y. Indeed, I do not believe that there are any longer any philosophical problems about Time; there is only the physical problem of determining the exact physical geometry of the four-dimensional continuum that we inhabit.

In this paper I have talked only about the relativistic aspects of the problem of physical time: there is, of course, also the problem of thermodynamics, and whether the Second Law does or does not explain the existence of "irreversible" processes (the so-called "problem of the direction of time"), and the problem of the existence or nonexistence of true irreversibilities in quantum mechanics, which, I gather, is currently under hot discussion. I have not talked about these problems.

("Time and Physical Geometry," Journal of Philosophy, 64, (1967) pp.240-247)

Although Putnam's principle that There Are No Privileged Observers is correct, there may exist preferred frames of reference that suggest solutions to some important problems, for example, the EPR Paradox.

Entanglement is a mysterious quantum phenomenon that seems capable of transmitting information over vast distances faster than the speed of light, a property called non-locality, first seen by Albert Einstein in 1905. Information physics shows that although information about probability (actually, about possibilities) comes into existence simultaneously at space-like separated points, no faster-than-light signaling is possible, since neither matter nor energy is transmitted.

The mysterious "collapse" of the wave function is a question about possibilities, probabilities, and actuality.

The collapse of the two-particle wave function in the EPR experiment is the same mystery as the one in the two-slit experiment, except that now there are two particles and they appear instantly and simultansously, despite their space-like separation. This can be seen by reformulating the EPR paradox using a preferred frame of reference in which the source of the entangled particles and the observers are at rest.

Almost every presentation of the EPR paradox begins with something like "Alice observes one particle..." and concludes with the question "How does the second particle get the information needed so that Bob's measurements correlate perfectly with Alice?"

There is a fundamental asymmetry in this framing of the EPR experiment. It is a surprise that Einstein, who was so good at seeing deep symmetries, did not consider how to remove the asymmetry.

Consider this reframing: Alice's measurement collapses the two-particle wave function. The two indistinguishable particles simultaneously appear at locations in a space-like separation. The frame of reference in which the source of the two entangled particles and the two experimenters are at rest is a preferred frame in the following sense.

As Einstein and Putnam knew very well, there are frames of reference moving with respect to the laboratory frame of the two observers in which the time order of the events can be reversed. In some moving frames Alice measures first, but in others Bob measures first.

If there is a preferred frame of reference, surely it is the one in which the origin of the two entangled particles is at rest. Assuming that Alice and Bob are also at rest in this preferred frame and equidistant from the origin, we arrive at the simple picture in which any measurement that causes the two-particle wave function to collapse makes both particles appear simultaneously at determinate places (just what is needed to conserve energy, momentum, angular momentum, and spin).

In the two-particle case (instead of just one particle making an appearance), when either particle is measured, we know instantly those properties of the other particle that satisfy the conservation laws, including its location equidistant from, but on the opposite side of, the source, and its other properties such as spin.

Let's look at an animation of the two-particle wave function expanding from the origin and what happens when, say, Alice makes a measurement.

We can also ask what happens if Bob is not at the same distance from the origin as Alice. This introduces a positional asymmetry. But there is still no time asymmetry from the point of view of the two-particle wave function collapse.

When Alice detects the particle (with say spin up), at that instant the other particle also becomes determinate (with spin down) at the same distance on the other side of the origin. It now continues, in that determinate state, to Bob's measuring apparatus.

Einstein asked whether the particle has a determinate position just before it is measured. Probably not, but we can say that before Bob's measurement the electron spin was determined from the moment the two-particle wave function collapsed. Recall that the two-particle wave function describing the indistinguishable particles cannot be separated into a product of two single-particle wave functions. When either particle is measured, they both become determinate.