Now though, experts in industry, academia, and government laboratories anticipate that semiconductor miniaturization won’t continue much longer—maybe 5 or 10 years. Making transistors smaller no longer yields the improvements it used to. The physical characteristics of small transistors caused clock speeds to stagnate more than a decade ago, which drove the industry to start building chips with multiple cores. But even multicore architectures must contend with increasing amounts of “dark silicon,” areas of the chip that must be powered off to avoid overheating.

Heroic efforts are being made within the semiconductor industry to try to keep miniaturization going. But no amount of investment can change the laws of physics. At some point—now not very far away—a new computer that simply has smaller transistors will no longer be any cheaper, faster, or more energy efficient than its predecessors. At that point, the progress of conventional semiconductor technology will stop.

What about unconventional semiconductor technology, such as carbon-nanotube transistors, tunneling transistors, or spintronic devices? Unfortunately, many of the same fundamental physical barriers that prevent today’s complementary metal-oxide-semiconductor (CMOS) technology from advancing very much further will still apply, in a modified form, to those devices. We might be able to eke out a few more years of progress, but if we want to keep moving forward decades down the line, new devices are not enough: We’ll also have to rethink our most fundamental notions of computation.

Let me explain. For the entire history of computing, our calculating machines have operated in a way that causes the intentional loss of some information (it’s destructively overwritten) in the process of performing computations. But for several decades now, we have known that it’s possible in principle to carry out any desired computation without losing information—that is, in such a way that the computation could always be reversed to recover its earlier state. This idea of reversible computing goes to the very heart of thermo­dynamics and information theory, and indeed it is the only possible way within the laws of physics that we might be able to keep improving the cost and energy efficiency of general-purpose computing far into the future.

In the past, reversible computing never received much attention. That’s because it’s very hard to implement, and there was little reason to pursue this great challenge so long as conventional technology kept advancing. But with the end now in sight, it’s time for the world’s best physics and engineering minds to commence an all-out effort to bring reversible computing to practical fruition.

The history of reversible computing begins with physicist Rolf Landauer of IBM, who published a paper in 1961 titled “Irreversibility and Heat Generation in the Computing Process.” In it, Landauer argued that the logically irreversible character of conventional computational operations has direct implications for the thermodynamic behavior of a device that is carrying out those operations.

Landauer’s reasoning can be understood by observing that the most fundamental laws of physics are reversible, meaning that if you had complete knowledge of the state of a closed system at some time, you could always—at least in principle—run the laws of physics in reverse and determine the system’s exact state at any previous time.

To better see that, consider a game of billiards—an ideal one with no friction. If you were to make a movie of the balls bouncing off one another and the bumpers, the movie would look normal whether you ran it backward or forward: The collision physics would be the same, and you could work out the future configuration of the balls from their past configuration or vice versa equally easily.

The same fundamental reversibility holds for quantum-scale physics. As a consequence, you can’t have a situation in which two different detailed states of any physical system evolve into the exact same state at some later time, because that would make it impossible to determine the earlier state from the later one. In other words, at the lowest level in physics, information cannot be destroyed.

The reversibility of physics means that we can never truly erase information in a computer. Whenever we overwrite a bit of information with a new value, the previous information may be lost for all practical purposes, but it hasn’t really been physically destroyed. Instead it has been pushed out into the machine’s thermal environment, where it becomes entropy—in essence, randomized information—and manifests as heat.

Returning to our billiards-game example, suppose that the balls, bumpers, and felt were not frictionless. Then, sure, two different initial configurations might end up in the same state—say, with the balls resting on one side. The frictional loss of information would then generate heat, albeit a tiny amount.

Today’s computers rely on erasing information all the time—so much so that every single active logic gate in conventional designs destructively overwrites its previous output on every clock cycle, wasting the associated energy. A conventional computer is, essentially, an expensive electric heater that happens to perform a small amount of computation as a side effect.

Back to the Future
Reversible computing is based on reversible physics, where no energy is lost to friction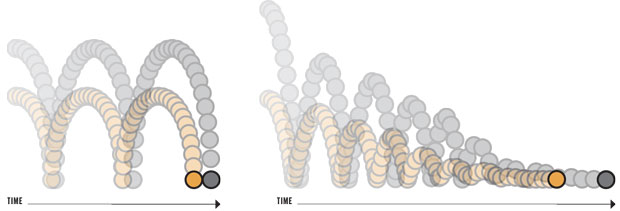

Illustration: James Provost
TWO IDEAL BALLS, perfectly elastic and free of internal friction, are dropped from different heights. They will then bounce back repeatedly to their original heights. At any point, the future or past velocity and position of a ball can be calculated based on its current velocity and position [left]. But if there is internal friction, the situation is no longer reversible: Both balls ultimately end up on the ground, and you cannot determine their past velocities and positions from their current ones [right]. Here, energy is wasted through the frictional generation of heat.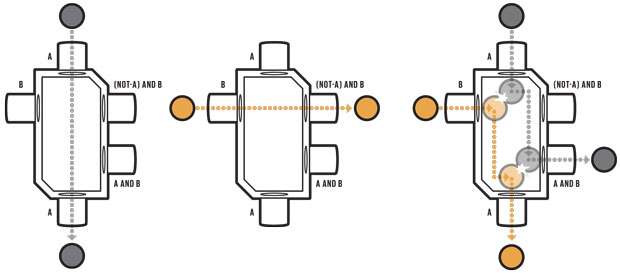

Illustration: James Provost
A LOGIC GATE could, in principle, be constructed from idealized balls and barriers. This billiard-ball AND gate has two inputs and three outputs. If a “true” is applied only to the “A” input (a ball entering from the top), then a “true” will appear on the “A” output (ball exiting from the bottom) [left]. If “true” is applied only to the “B” input (a ball entering from the left), then a “true” will appear only on the “(NOT-A) AND B” output (ball exiting to the right) [middle]. If “true” is applied to both inputs, then a “true” will appear on both the “A” and “A AND B” outputs [right].
How much heat is produced? Landauer’s conclusion, which has since been experimentally confirmed, was that each bit erasure must dissipate at least 17-⁠thousandths of an electron volt at room temperature. This is a very small amount of energy, but given all the operations that take place in a computer, it adds up. Present-day CMOS technology actually does much worse than Landauer calculated, dissipating something in the neighborhood of 5,000 electron volts per bit erased. Standard CMOS designs could be improved in this regard, but they won’t ever be able to get much below about 500 eV of energy lost per bit erased, still far from Landauer’s lower limit.

Can we do better? Landauer began to consider this question in his 1961 paper where he gave examples of logically reversible operations, meaning ones that transform computational states in such a way that each possible initial state yields some unique final state. Such operations could, in principle, be carried out in a thermodynamically reversible way, in which case any energy associated with the ­information-bearing signals in the system would not necessarily have to be dissipated as heat but could instead potentially be reused for subsequent operations.

To prove this approach could still do everything a conventional computer could do, Landauer also noted that any desired logically irreversible computational operation could be embedded in a reversible one, by simply setting aside any information that was no longer needed, rather than erasing it. But Landauer originally thought that doing this was only delaying the inevitable, because the information would still need to be erased eventually, when the available memory filled up.

It was left to Landauer’s younger colleague, Charles Bennett, to show in 1973 that it is possible to construct fully reversible computers capable of performing any computation without quickly filling up memory with temporary data. The trick is to undo the operations that produced the intermediate results. This would allow any temporary memory to be reused for subsequent computations without ever having to erase or overwrite it. In this way, reversible computations, if implemented on the right hardware, could, in principle, circumvent Landauer’s limit.

Unfortunately, Bennett’s idea of using reversible computing to make computation far more energy efficient languished in academic backwaters for many years. The problem was that it’s really hard to engineer a system that does something computationally interesting without inadvertently incurring a significant amount of entropy increase with each operation. But technology has improved, and the need to minimize energy use is now acute. So some researchers are once again looking to reversible computing to save energy.

What would a reversible computer look like? The first detailed attempts to describe an efficient physical mechanism for reversible computing were carried out in the late 1970s and early 1980s by Edward Fredkin and his colleague Tommaso Toffoli in their Information Mechanics research group at MIT.

As a proof of concept, Fredkin and Toffoli proposed that reversible operations could, in principle, be carried out by idealized electronic circuits that used inductors to shuttle charge packets back and forth between capacitors. With no resistors damping the flow of energy, these circuits were theoretically lossless. In the mechanical domain, Fredkin and Toffoli imagined rigid spheres bouncing off of each other and fixed barriers in narrowly constrained trajectories, not unlike the frictionless billiards game I described earlier.

Unfortunately, these idealized systems couldn’t be built in practice. But these investigations led to the development of two abstract computational primitives, now known as the Fredkin gate and the Toffoli gate, which became the foundation of much of the subsequent theoretical work in reversible computing. Any computation can be performed using these gates, which operate on three input bits, transforming them into unique final configurations of three output bits.

Meanwhile, other researchers at such places as Caltech, Rutgers, the University of Southern California, and Xerox PARC continued to explore possible electronic implementations. They called their circuits “adiabatic” after the ­idealized thermodynamic regime in which energy is barred from leaving the system as heat.

These ideas later found fertile ground back at MIT, where in 1993 a graduate student named Saed Younis in Tom Knight’s group showed for the first time that adiabatic circuits could be used to implement fully reversible logic. Later students in the group, including Carlin Vieri and I, built on that foundation to design and construct fully reversible processors of various types in CMOS as simple proofs of concept. This work established that there were no fundamental barriers preventing the entire discipline of computer architecture from being translated to the reversible realm.

Meanwhile, other researchers had been exploring alternative approaches to implementing reversible computing that were not based on semiconductor electronics at all. In the early 1990s, nanotechnology visionary K. Eric Drexler produced detailed designs for reversible nanomechanical logic devices made from diamond-like materials. Over the decades, Russian and Japanese researchers had been developing reversible superconducting electronic devices, such as the similarly named (but distinct) parametric ­quantron and quantum flux parametron. And a group at the ­University of Notre Dame was studying how to use interacting single electrons in arrays of quantum dots. To those of us who were working on reversible computing in the 1990s, it seemed that, based on the wide range of possible hardware that had already been proposed, some kind of practical reversible computing technology might not be very far away.

Alas, the idea was still ahead of its time. Conventional semiconductor technology improved rapidly through the 1990s and early 2000s, and so the field of reversible computing mostly languished. Nevertheless, some progress was made. For example, in 2004 Krishna Natarajan (a student I was advising at the University of Florida) and I showed in detailed simulations that a new and simplified family of circuits for reversible computing called two-level adiabatic logic, or 2LAL, could dissipate as little as 1 eV of energy per transistor per cycle—about 0.001 percent of the energy normally used by logic signals in that generation of CMOS. Still, a practical reversible computer has yet to be built using this or other approaches.

There’s not much time left to develop reversible machines, because progress in conventional semiconductor technology could grind to a halt soon. And if it does, the industry could stagnate, making forward progress that much more difficult. So the time is indeed ripe now to pursue this technology, as it will probably take at least a decade for reversible computers to become practical.

The most crucial need is for new reversible device technologies. Conventional CMOS transistors—especially the smallest, state-of-the-art ones—leak too much current to make very efficient adiabatic circuits. Larger transistors based on older manufacturing technology leak less, but they’d have to be operated quite slowly, which means many devices would need to be used to speed up computation through parallel operation. Stacking them in layers could yield compact and energy-efficient adiabatic circuits, but at the moment such 3D fabrication is still quite costly. And CMOS may be a dead end in any case.

Computing With Tiny Link Logic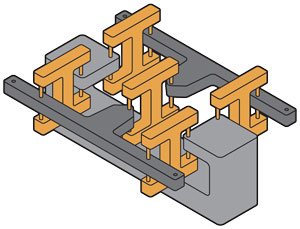

Illustration: James Provost
Ralph Merkle and his colleagues envision doing computations using nanomechanical “link logic,” a building block for which is shown here. That device contains two movable bars [dark gray], connected in such a way that only one bar at a time can be shifted from its central position. These bars would measure a few hundred atoms across, and their pivot points would be nearly frictionless. So great numbers of them connected together in the proper fashion could perform calculations, just as transistors do today. The difference is that a tiny link-logic system would be reversible.

Fortunately, there are some promising alternatives. One is to use fast superconducting electronics to build reversi­ble circuits, which have already been shown to dissipate less energy per device than the Landauer limit when operated reversibly. Advances in this realm have been made by researchers at Yokohama National University, Stony Brook University, and Northrop Grumman. Meanwhile, a team led by Ralph Merkle at the Institute for Molecular Manufacturing in Palo Alto, Calif., has designed reversible nanometer-scale molecular machines, which in theory could consume one-hundred-billionth the energy of today’s computing technology while still switching on nanosecond timescales. The rub is that the technology to manufacture such atomically precise devices still needs to be invented.

Whether or not these particular approaches pan out, physi­cists who are working on developing new device concepts need to keep the goal of reversible operation in mind. After all, that is the only way that any new computing substrate can possibly surpass the practical capabilities of end-of-line CMOS technology by many orders of magnitude, as opposed to only a few at most.

To be clear, reversible computing is by no means easy. Indeed, the engineering hurdles are enormous. Achieving efficient reversible computing with any kind of technology will likely require a thorough overhaul of our entire chip-design infrastructure. We’ll also have to retrain a large part of the digital-engineering workforce to use the new design methodologies. I would guess that the total cost of all of the new investments in education, research, and development that will be required in the coming decades will most likely run well up into the billions of dollars. It’s a future-computing moon shot.

But in my opinion, the difficulty of these challenges would be a very poor excuse for not facing up to them. At this moment, we’ve arrived at a historic juncture in the evolution of computing technology, and we must choose a path soon.

If we continue on our present course, this would amount to giving up on the future of computing and accepting that the energy efficiency of our hardware will soon plateau. Even such unconventional concepts as analog or spike-based neural computing will eventually reach a limit if they are not designed to also be reversible. And even a quantum-computing breakthrough would only help to significantly speed up a few highly specialized classes of computations, not computing in general.

But if we decide to blaze this new trail of reversible computing, we may continue to find ways to keep improving computation far into the future. Physics knows no upper limit on the amount of reversible computation that can be performed using a fixed amount of energy. So as far as we know, an unbounded future for computing awaits us, if we are bold enough to seize it.

This article appears in the September 2017 print issue as “Throwing Computing Into Reverse.”

About the Author
Michael P. Frank is a senior member of the technical staff at Sandia National Laboratories, in Albuquerque, where he studies advanced technologies for computation.