MacKay contributed to the London Symposia on Information Theory and attended the eighth Macy Conference on Cybernetics in New York in 1951 where he met Gregory Bateson, Warren McCulloch, I. A. Richards, and Claude Shannon.

Roman Jakobson, who attended the eighth Macy Conference, and attended some London Symposia, encouraged MacKay to publish a collection of his several essays on Information and Meaning that had been published between 1950 and 1960.

They contain the first, and in many ways, the clearest account of how to add "meaning" to information theory, in light of Shannon's warning that his work was a theory of "communication" only, completely independent of the meaning in a message. Here is Shannon's famous sender-receiver diagram.

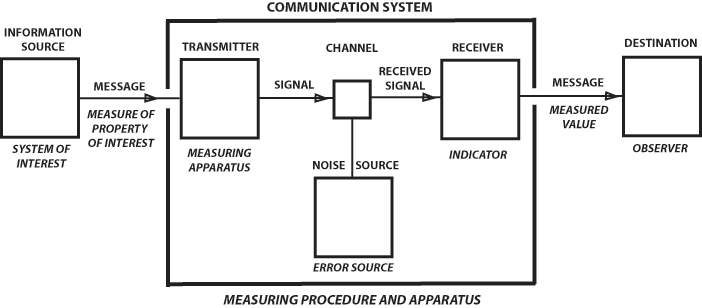
Jakobson added the "context" of a message to Shannon's diagram, so was in an excellent position to appreciate MacKay's work. Here is Jakobson's addition of context.

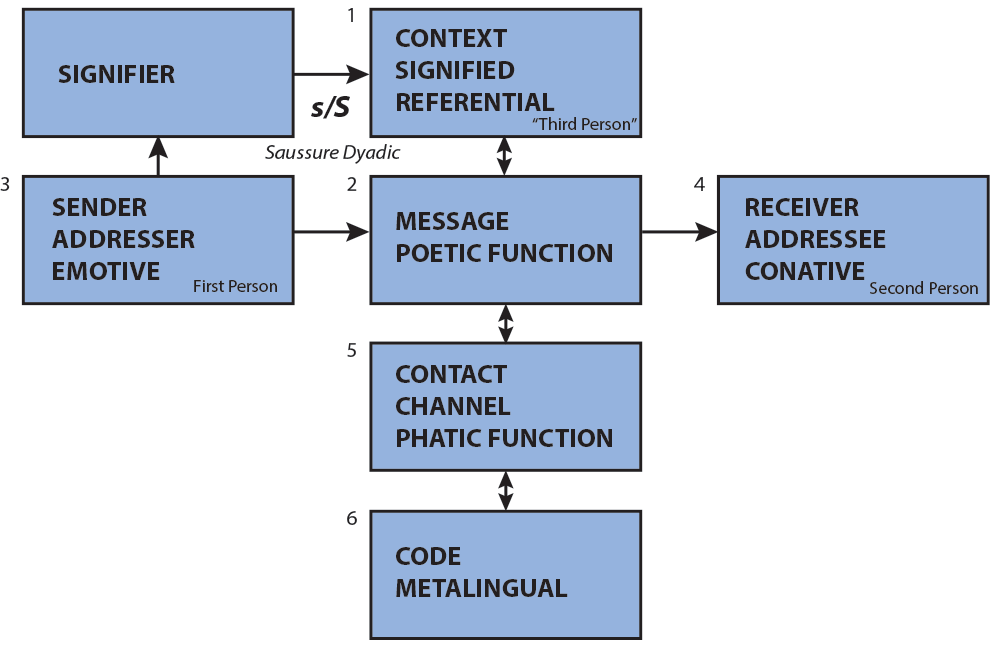
Context was perhaps Jakobson's most important addition to semiotics. Adding context gives us the difference between semantics (the standard dictionary meaning of a word according to the normal "rules" of the language) versus pragmatics, the meaning that may be intended by the sender, or should be inferred by the receiver/interpreter because of the current situation. Jakobson calls this contextual information "denotative," "cognitive," "referential," the "leading task" of a message. Context-dependence alters the "meaning" to suit the purpose of a communication.

MacKay's earliest work, at the end of World War II, behaviour of electrical pulses over extremely short intervals of time. He wrote

Inevitably, one came up against fundamental physical limits to the accuracy of measurement. Typically, these limits seemed to be related in a complementary way, so that one of them could be widened only at the expense of a narrowing of another. An increase in time-resolving power, for example, seemed always to be bought at the expense of a reduction in frequency-resolving power; an improvement in signal-to-noise ratio was often inseparable from a reduction in time-resolving power, and so on. The art of physical measurement seemed to be ultimately a matter of compromise, of choosing between reciprocally related uncertainties.

I was struck by a possible analogy between this situation and the one in atomic physics expressed by Heisenberg's well-known 'Principle of Uncertainty'. This states that the momentum (p) and position (q ) of a particle can never be exactly determined at the same instant. The smaller the imprecision (Δp) in p, the larger must be the imprecision (Δq ) in q and vice versa. In fact, the product ΔpΔq can never be less than Planck's Constant h, the 'quantum of action'. Action (energy x time) is thus the fundamental physical quantity whose 'atomicity' underlies the compromise- relation expressed in Heisenberg's Principle.

(Information, Mechanism, and Meaning, 1969, p.1)

MacKay learned a few years later that Dennis Gabor derived a similar relation in 1946. He published a classic paper entitled 'Theory of Communication', in which the Fourier transform theory used in wave mechanics was applied to the frequency-time (f-t) domain of the communication engineer, with the suggestion that a signal occupying an elementary area of Δf Δt = 1/2 could be regarded as a "unit of information", which he called a "logon".

Much earlier, in 1935, the statistician R. A. Fisher had proposed a measure of the "information' in a statistical sample, which in the simplest case amounted to the reciprocal of the variance.

MacKay was not sure how Gabor's and Fisher's concepts fitted into the theory of information, but

on reflection it became apparent that they were in fact examples of ' structural' and ' metrical' measures, respectively. Gabor's logons, each occupying an area Δf Δt = 1/2 in the f - t plane, represented the logical dimensions of his communication signals. They belonged to the same family as the ' structural units' that occupy an analogous elementary area (the Airy disc) in the focal plane of a microscope, or of a radar aerial. It thus seemed appropriate, with Gabor's blessing, to give the term 'logon-content' a more general definition, as the measure of the logical dimensionality of representations of any form, whether spatial or temporal.

Fisher's measure, which is additive for averaged samples, invited an equally straightforward interpretation as an index of 'weight of evidence'. If we define (arbitrarily but reasonably) a unit or quantum of metrical information (termed a 'metron') as the weight of evidence that gives a probability of \ to the corresponding proposition, Fisher's 'amount of information' becomes simply proportional to the number of such units supplied by the evidence in question

(Information, Mechanism, and Meaning, 1969, p.4)