|
Topics
Introduction
Problems Freedom Knowledge Mind Life Chance Quantum Entanglement Scandals Philosophers Mortimer Adler Rogers Albritton Alexander of Aphrodisias Samuel Alexander William Alston Anaximander G.E.M.Anscombe Anselm Louise Antony Thomas Aquinas Aristotle David Armstrong Harald Atmanspacher Robert Audi Augustine J.L.Austin A.J.Ayer Alexander Bain Mark Balaguer Jeffrey Barrett William Barrett William Belsham Henri Bergson George Berkeley Isaiah Berlin Richard J. Bernstein Bernard Berofsky Robert Bishop Max Black Susan Blackmore Susanne Bobzien Emil du Bois-Reymond Hilary Bok Laurence BonJour George Boole Émile Boutroux Daniel Boyd F.H.Bradley C.D.Broad Michael Burke Jeremy Butterfield Lawrence Cahoone C.A.Campbell Joseph Keim Campbell Rudolf Carnap Carneades Nancy Cartwright Gregg Caruso Ernst Cassirer David Chalmers Roderick Chisholm Chrysippus Cicero Tom Clark Randolph Clarke Samuel Clarke Anthony Collins August Compte Antonella Corradini Diodorus Cronus Jonathan Dancy Donald Davidson Mario De Caro Democritus William Dembski Brendan Dempsey Daniel Dennett Jacques Derrida René Descartes Richard Double Fred Dretske Curt Ducasse John Earman Laura Waddell Ekstrom Epictetus Epicurus Austin Farrer Herbert Feigl Arthur Fine John Martin Fischer Frederic Fitch Owen Flanagan Luciano Floridi Philippa Foot Alfred Fouilleé Harry Frankfurt Richard L. Franklin Bas van Fraassen Michael Frede Gottlob Frege Peter Geach Edmund Gettier Carl Ginet Alvin Goldman Gorgias Nicholas St. John Green Niels Henrik Gregersen H.Paul Grice Ian Hacking Ishtiyaque Haji Stuart Hampshire W.F.R.Hardie Sam Harris William Hasker R.M.Hare Georg W.F. Hegel Martin Heidegger Heraclitus R.E.Hobart Thomas Hobbes David Hodgson Shadsworth Hodgson Baron d'Holbach Ted Honderich Pamela Huby David Hume Ferenc Huoranszki Frank Jackson William James Lord Kames Robert Kane Immanuel Kant Tomis Kapitan Walter Kaufmann Jaegwon Kim William King Hilary Kornblith Christine Korsgaard Saul Kripke Thomas Kuhn Andrea Lavazza James Ladyman Christoph Lehner Keith Lehrer Gottfried Leibniz Jules Lequyer Leucippus Michael Levin Joseph Levine George Henry Lewes C.I.Lewis David Lewis Peter Lipton C. Lloyd Morgan John Locke Michael Lockwood Arthur O. Lovejoy E. Jonathan Lowe John R. Lucas Lucretius Alasdair MacIntyre Ruth Barcan Marcus Tim Maudlin James Martineau Nicholas Maxwell Storrs McCall Hugh McCann Colin McGinn Michael McKenna Brian McLaughlin John McTaggart Paul E. Meehl Uwe Meixner Alfred Mele Trenton Merricks John Stuart Mill Dickinson Miller G.E.Moore Ernest Nagel Thomas Nagel Otto Neurath Friedrich Nietzsche John Norton P.H.Nowell-Smith Robert Nozick William of Ockham Timothy O'Connor Parmenides David F. Pears Charles Sanders Peirce Derk Pereboom Steven Pinker U.T.Place Plato Karl Popper Porphyry Huw Price H.A.Prichard Protagoras Hilary Putnam Willard van Orman Quine Frank Ramsey Ayn Rand Michael Rea Thomas Reid Charles Renouvier Nicholas Rescher C.W.Rietdijk Richard Rorty Josiah Royce Bertrand Russell Paul Russell Gilbert Ryle Jean-Paul Sartre Kenneth Sayre T.M.Scanlon Moritz Schlick John Duns Scotus Albert Schweitzer Arthur Schopenhauer John Searle Wilfrid Sellars David Shiang Alan Sidelle Ted Sider Henry Sidgwick Walter Sinnott-Armstrong Peter Slezak J.J.C.Smart Saul Smilansky Michael Smith Baruch Spinoza L. Susan Stebbing Isabelle Stengers George F. Stout Galen Strawson Peter Strawson Eleonore Stump Francisco Suárez Richard Taylor Kevin Timpe Mark Twain Peter Unger Peter van Inwagen Manuel Vargas John Venn Kadri Vihvelin Voltaire G.H. von Wright David Foster Wallace R. Jay Wallace W.G.Ward Ted Warfield Roy Weatherford C.F. von Weizsäcker William Whewell Alfred North Whitehead David Widerker David Wiggins Bernard Williams Timothy Williamson Ludwig Wittgenstein Susan Wolf Xenophon Scientists David Albert Philip W. Anderson Michael Arbib Bobby Azarian Walter Baade Bernard Baars Jeffrey Bada Leslie Ballentine Marcello Barbieri Jacob Barandes Julian Barbour Horace Barlow Gregory Bateson Jakob Bekenstein John S. Bell Mara Beller Charles Bennett Ludwig von Bertalanffy Susan Blackmore Margaret Boden David Bohm Niels Bohr Ludwig Boltzmann John Tyler Bonner Emile Borel Max Born Satyendra Nath Bose Walther Bothe Jean Bricmont Hans Briegel Leon Brillouin Daniel Brooks Stephen Brush Henry Thomas Buckle S. H. Burbury Melvin Calvin William Calvin Donald Campbell John O. Campbell Sadi Carnot Sean B. Carroll Anthony Cashmore Eric Chaisson Gregory Chaitin Jean-Pierre Changeux Rudolf Clausius Arthur Holly Compton John Conway Simon Conway-Morris Peter Corning George Cowan Jerry Coyne John Cramer Francis Crick E. P. Culverwell Antonio Damasio Olivier Darrigol Charles Darwin Paul Davies Richard Dawkins Terrence Deacon Lüder Deecke Richard Dedekind Louis de Broglie Stanislas Dehaene Max Delbrück Abraham de Moivre David Depew Bernard d'Espagnat Paul Dirac Theodosius Dobzhansky Hans Driesch John Dupré John Eccles Arthur Stanley Eddington Gerald Edelman Paul Ehrenfest Manfred Eigen Albert Einstein George F. R. Ellis Walter Elsasser Hugh Everett, III Franz Exner Richard Feynman R. A. Fisher David Foster Joseph Fourier George Fox Philipp Frank Steven Frautschi Edward Fredkin Augustin-Jean Fresnel Karl Friston Benjamin Gal-Or Howard Gardner Lila Gatlin Michael Gazzaniga Nicholas Georgescu-Roegen GianCarlo Ghirardi J. Willard Gibbs James J. Gibson Nicolas Gisin Paul Glimcher Thomas Gold A. O. Gomes Brian Goodwin Julian Gough Joshua Greene Dirk ter Haar Jacques Hadamard Mark Hadley Ernst Haeckel Patrick Haggard J. B. S. Haldane Stuart Hameroff Augustin Hamon Sam Harris Ralph Hartley Hyman Hartman Jeff Hawkins John-Dylan Haynes Donald Hebb Martin Heisenberg Werner Heisenberg Hermann von Helmholtz Grete Hermann John Herschel Francis Heylighen Basil Hiley Art Hobson Jesper Hoffmeyer John Holland Don Howard John H. Jackson Ray Jackendoff Roman Jakobson E. T. Jaynes William Stanley Jevons Pascual Jordan Eric Kandel Ruth E. Kastner Stuart Kauffman Martin J. Klein William R. Klemm Christof Koch Simon Kochen Hans Kornhuber Stephen Kosslyn Daniel Koshland Ladislav Kovàč Leopold Kronecker Bernd-Olaf Küppers Rolf Landauer Alfred Landé Pierre-Simon Laplace Karl Lashley David Layzer Joseph LeDoux Gerald Lettvin Michael Levin Gilbert Lewis Benjamin Libet David Lindley Seth Lloyd Werner Loewenstein Hendrik Lorentz Josef Loschmidt Alfred Lotka Ernst Mach Donald MacKay Henry Margenau Lynn Margulis Owen Maroney David Marr Humberto Maturana James Clerk Maxwell John Maynard Smith Ernst Mayr John McCarthy Barbara McClintock Warren McCulloch N. David Mermin George Miller Stanley Miller Ulrich Mohrhoff Jacques Monod Vernon Mountcastle Gerd B. Müller Emmy Noether Denis Noble Donald Norman Travis Norsen Howard T. Odum Alexander Oparin Abraham Pais Howard Pattee Wolfgang Pauli Massimo Pauri Wilder Penfield Roger Penrose Massimo Pigliucci Steven Pinker Colin Pittendrigh Walter Pitts Max Planck Susan Pockett Henri Poincaré Michael Polanyi Daniel Pollen Ilya Prigogine Hans Primas Giulio Prisco Zenon Pylyshyn Henry Quastler Adolphe Quételet Pasco Rakic Nicolas Rashevsky Lord Rayleigh Frederick Reif Jürgen Renn Giacomo Rizzolati A.A. Roback Emil Roduner Juan Roederer Robert Rosen Frank Rosenblatt Jerome Rothstein David Ruelle David Rumelhart Michael Ruse Stanley Salthe Robert Sapolsky Tilman Sauer Ferdinand de Saussure Jürgen Schmidhuber Erwin Schrödinger Aaron Schurger Sebastian Seung Thomas Sebeok Franco Selleri Claude Shannon James A. Shapiro Charles Sherrington Abner Shimony Herbert Simon Dean Keith Simonton Edmund Sinnott B. F. Skinner Lee Smolin Ray Solomonoff Herbert Spencer Roger Sperry John Stachel Kenneth Stanley Henry Stapp Ian Stewart Tom Stonier Antoine Suarez Leonard Susskind Leo Szilard Max Tegmark Teilhard de Chardin Libb Thims William Thomson (Kelvin) Richard Tolman Giulio Tononi Peter Tse Alan Turing Robert Ulanowicz C. S. Unnikrishnan Nico van Kampen Francisco Varela Vlatko Vedral Vladimir Vernadsky Clément Vidal Mikhail Volkenstein Heinz von Foerster Richard von Mises John von Neumann Jakob von Uexküll C. H. Waddington Sara Imari Walker James D. Watson John B. Watson Daniel Wegner Steven Weinberg August Weismann Paul A. Weiss Herman Weyl John Wheeler Jeffrey Wicken Wilhelm Wien Norbert Wiener Eugene Wigner E. O. Wiley E. O. Wilson Günther Witzany Carl Woese Stephen Wolfram H. Dieter Zeh Semir Zeki Ernst Zermelo Wojciech Zurek Konrad Zuse Fritz Zwicky Presentations ABCD Harvard (ppt) Biosemiotics Free Will Mental Causation James Symposium CCS25 Talk Evo Devo September 12 Evo Devo October 2 Evo Devo Goodness Evo Devo Davies Nov12 |
Probability and Uncertainty
Chapter 6 of The Character of Physical Law (annotated)
- the Quantum Mechanical View of Nature
In 1925 quantum mechanics discovered the equations that let us calculate physical properties to extraordinary accuracy, but the founders did not provide us with an intuitive picture of what is going on at the quantum level
This growing confusion was resolved in 1925 or 1926 with the advent of the correct equations for quantum mechanics. Now we know how the electrons and light behave. But what can I call it? If I say they behave like particles I give the wrong impression; also if I say they behave like waves. They behave in their own inimitable way, which technically could be called a quantum mechanical way. They behave in a way that is like nothing that you have ever seen before. Your experience with things that you have seen before is incomplete. The behaviour of things on a very tiny scale is simply different. An atom does not behave like a weight hanging on a spring and oscillating. Nor does it behave like a miniature representation of the solar system with little planets going around in orbits. Nor does it appear to be somewhat like a cloud or fog of some sort surrounding the nucleus. It behaves like nothing you have ever seen before.
There is one simplification at least. Electrons behave in this respect in exactly the same way as photons; they are both screwy, but in exactly the same way.
How they behave, therefore, takes a great deal of imagination to appreciate, because we are going to describe something which is different from anything you know about. In that respect at least this is perhaps the most difficult lecture of the series, in the sense that it is abstract, in the sense that it is not close to experience. I cannot avoid that. Were I to give a series of lectures on the character of physical law, and to leave out from this series the description of the actual behaviour of particles on a small scale, I would certainly not be doing the job. This thing is completely characteristic of all of the particles of nature, and of a universal character, so if you want to hear about the character of physical law it is essential to talk about this particular aspect.
It will be difficult. But the difficulty really is psychological and exists in the perpetual torment that results from your saying to yourself, 'But how can it be like that?' which is a reflection of uncontrolled but utterly vain desire to see it in terms of something familiar. I will not describe it in terms of an analogy with something familiar; I will simply describe it. There was a time when the newspapers said that only twelve men understood the theory of relativity. I do not believe there ever was such a time. There might have been a time when only one man did, because he was the only guy who caught on, before he wrote his paper. But after people read the paper a lot of people understood the theory of relativity in some way or other, certainly more than twelve.
"nobody understands quantum mechanics"
On the other hand, I think I can safely say that nobody understands quantum mechanics. So do not take the lecture too seriously, feeling that you really have to understand in terms of some model what I am going to describe, but just relax and enjoy it. I am going to tell you what nature behaves like. If you will simply admit that maybe she does behave like this, you will find her a delightful, entrancing thing. Do not keep saying to yourself, if you can possibly avoid it, 'But how can it be like that?' because you will get 'down the drain', into a blind alley from which nobody has yet escaped. Nobody knows how it can be like that.
So then, let me describe to you the behaviour of electrons or of photons in their typical quantum mechanical way. I am going to do this by a mixture of analogy and contrast.
If I made it pure analogy we would fail; it must be by analogy and contrast with things which are familiar to you. So I make it by analogy and contrast, first to the behaviour of particles, for which I will use bullets, and second to the behaviour of waves, for which I will use water waves. What I am going to do is to invent a particular experiment and first tell you what the situation would be in that experiment using particles, then what you would expect to happen if waves were involved, and finally what happens when there are actually electrons or photons in the system.
Watch this famous Feynman quote We will show that the (one) mystery of quantum mechanics is how mere "probabilities" (immaterial information) can causally control (statistically) the positions of material particles
I will take just this one experiment, which has been designed to contain all of the mystery of quantum mechanics, to put you up against the paradoxes and mysteries and peculiarities of nature one hundred per cent. Any other situation in quantum mechanics, it turns out, can always be explained by saying, 'You remember the case of the experiment with the two holes ? It's the same thing'. I am going to tell you about the experiment with the two holes. It does contain the general mystery; I am avoiding nothing; I am baring nature in her most elegant and difficult form.
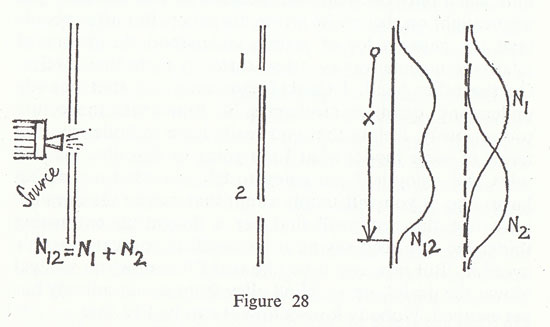 We start with bullets (fig. 28). Suppose that we have some source of bullets, a machine gun, and in front of it a plate with a hole for the bullets to come through, and this plate
is armour plate. A long distance away we have a second plate which has two holes in it — that is the famous two-hole business. I am going to talk a lot about these holes, so I will call them hole No. 1 and hole No. 2. You can imagine round holes in three dimensions — the drawing is just a cross section. A long distance away again we have another screen which is just a backstop of some sort on which we can put in various places a detector, which in the case of bullets is a box of sand into which the bullets will be caught so that we can count them. I am going to do experiments in which I count how many bullets come into this detector or box of sand when the box is in different positions, and to describe that I will measure the distance of the box from somewhere, and call that distance 'x', and I will talk about what happens when you change 'x', which means only that you move the detector box up and down. First I would like to make a few modifications from real bullets, in three idealizations. The first is that the machine gun is very shaky and wobbly and the bullets go in various directions, not just exactly straight on; they can ricochet off the edges of the holes in the armour plate. Secondly, we should say, although this is not very important, that the bullets have all the same speed or energy. The most important idealization in which this situation differs from real bullets is that I want these bullets to be absolutely indestructible, so that what we find in the box is not pieces of lead, of some bullet that broke in half, but we get the whole bullet. Imagine indestructible bullets, or hard bullets and soft armour plate.
The first thing that we shall notice about bullets is that the things that arrive come in lumps. When the energy comes it is all in one bulletful, one bang. If you count the bullets, there are one, two, three, four bullets; the things come in lumps. They are of equal size, you suppose, in this case, and when a thing comes into the box it is either all in the box or it is not in the box. Moreover, if I put up two boxes I never get two bullets in the boxes at the same time, presuming that the gun is not going off too fast and I have enough time between them to see. Slow down the gun so it goes off very slowly, then look very quickly in the two boxes, and you will never get two bullets at the same time in the two boxes, because a bullet is a single identifiable lump.
Now what I am going to measure is how many bullets arrive on the average over a period of time. Say we wait an hour, and we count how many bullets are in the sand and average that. We take the number of bullets that arrive per hour, and we can call that the probability of arrival, because it just gives the chance that a bullet going through a slit arrives in the particular box. The number of bullets that arrive in the box will vary of course as I vary 'x'. On the diagram I have plotted horizontally the number of bullets that I get if I hold the box in each position for an hour. I shall get a curve that will look more or less like curve N12 because when the box is behind one of the holes it gets a lot of bullets, and if it is a little out of line it does not get as many, they have to bounce off the edges of the holes, and eventually the curve disappears. The curve looks like curve N12, and the number that we get in an hour when both holes are open I will call N12 which merely means the number which arrive through hole No. 1 and hole No. 2.
I must remind you that the number that I have plotted does not come in lumps. It can have any size it wants. It can be two and a half bullets in an hour, in spite of the fact that bullets come in lumps. All I mean by two and a half bullets per hour is that if you run for ten hours you will get twenty-five bullets, so on the average it is two and a half bullets. I am sure you are all familiar with the joke about the average family in the United States seeming to have two and a half children. It does not mean that there is a half child in any family — children come in lumps. Nevertheless, when you take the average number per family it can be any number whatsoever, and in the same way this number N12, which is the number of bullets that arrive in the container per hour, on the average, need not be an integer. What we measure is the probability of arrival, which is a technical term for the average number that arrive in a given length of time.
Finally, if we analyse the curve N12 we can interpret it very nicely as the sum of two curves, one which will represent what I will call N1, the number which will come if hole No. 2 is closed by another piece of armour plate in front, and N2, the number which will come through hole No. 2 alone, if hole No. 1 is closed. We discover now a very important law, which is that the number that arrive with both holes open is the number that arrive by coming through hole No. 1, plus the number that come through hole No. 2. This proposition, the fact that all you have to do is to add these together, I call `no interference'.
We start with bullets (fig. 28). Suppose that we have some source of bullets, a machine gun, and in front of it a plate with a hole for the bullets to come through, and this plate
is armour plate. A long distance away we have a second plate which has two holes in it — that is the famous two-hole business. I am going to talk a lot about these holes, so I will call them hole No. 1 and hole No. 2. You can imagine round holes in three dimensions — the drawing is just a cross section. A long distance away again we have another screen which is just a backstop of some sort on which we can put in various places a detector, which in the case of bullets is a box of sand into which the bullets will be caught so that we can count them. I am going to do experiments in which I count how many bullets come into this detector or box of sand when the box is in different positions, and to describe that I will measure the distance of the box from somewhere, and call that distance 'x', and I will talk about what happens when you change 'x', which means only that you move the detector box up and down. First I would like to make a few modifications from real bullets, in three idealizations. The first is that the machine gun is very shaky and wobbly and the bullets go in various directions, not just exactly straight on; they can ricochet off the edges of the holes in the armour plate. Secondly, we should say, although this is not very important, that the bullets have all the same speed or energy. The most important idealization in which this situation differs from real bullets is that I want these bullets to be absolutely indestructible, so that what we find in the box is not pieces of lead, of some bullet that broke in half, but we get the whole bullet. Imagine indestructible bullets, or hard bullets and soft armour plate.
The first thing that we shall notice about bullets is that the things that arrive come in lumps. When the energy comes it is all in one bulletful, one bang. If you count the bullets, there are one, two, three, four bullets; the things come in lumps. They are of equal size, you suppose, in this case, and when a thing comes into the box it is either all in the box or it is not in the box. Moreover, if I put up two boxes I never get two bullets in the boxes at the same time, presuming that the gun is not going off too fast and I have enough time between them to see. Slow down the gun so it goes off very slowly, then look very quickly in the two boxes, and you will never get two bullets at the same time in the two boxes, because a bullet is a single identifiable lump.
Now what I am going to measure is how many bullets arrive on the average over a period of time. Say we wait an hour, and we count how many bullets are in the sand and average that. We take the number of bullets that arrive per hour, and we can call that the probability of arrival, because it just gives the chance that a bullet going through a slit arrives in the particular box. The number of bullets that arrive in the box will vary of course as I vary 'x'. On the diagram I have plotted horizontally the number of bullets that I get if I hold the box in each position for an hour. I shall get a curve that will look more or less like curve N12 because when the box is behind one of the holes it gets a lot of bullets, and if it is a little out of line it does not get as many, they have to bounce off the edges of the holes, and eventually the curve disappears. The curve looks like curve N12, and the number that we get in an hour when both holes are open I will call N12 which merely means the number which arrive through hole No. 1 and hole No. 2.
I must remind you that the number that I have plotted does not come in lumps. It can have any size it wants. It can be two and a half bullets in an hour, in spite of the fact that bullets come in lumps. All I mean by two and a half bullets per hour is that if you run for ten hours you will get twenty-five bullets, so on the average it is two and a half bullets. I am sure you are all familiar with the joke about the average family in the United States seeming to have two and a half children. It does not mean that there is a half child in any family — children come in lumps. Nevertheless, when you take the average number per family it can be any number whatsoever, and in the same way this number N12, which is the number of bullets that arrive in the container per hour, on the average, need not be an integer. What we measure is the probability of arrival, which is a technical term for the average number that arrive in a given length of time.
Finally, if we analyse the curve N12 we can interpret it very nicely as the sum of two curves, one which will represent what I will call N1, the number which will come if hole No. 2 is closed by another piece of armour plate in front, and N2, the number which will come through hole No. 2 alone, if hole No. 1 is closed. We discover now a very important law, which is that the number that arrive with both holes open is the number that arrive by coming through hole No. 1, plus the number that come through hole No. 2. This proposition, the fact that all you have to do is to add these together, I call `no interference'.
N12 = N1 + N2 (no interference).
That is for bullets, and now we have done with bullets we begin again, this time with water waves (fig. 29).
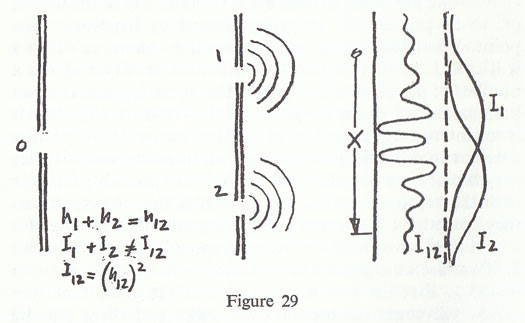 The source is now a big mass of stuff which is being shaken up and down in the water. The armour plate becomes a long line of barges or jetties with a gap in the water in between. Perhaps it would be better to do it with ripples than with big ocean waves; it sounds more sensible. I wiggle my finger up and down to make waves, and I have a little piece of wood as a barrier with a hole for the ripples to come through. Then I have a second barrier with two holes, and finally a detector. What do I do with the detector? What the detector detects is how much the water is jiggling. For instance, I put a cork in the water and measure how it moves up and down, and what I am going to measure in fact is the energy of the agitation of the cork, which is exactly proportional to the energy carried by the waves. One other thing: the jiggling is made very regular and perfect so that the waves are all the same space from one another. One thing that is important for water waves is that the thing we are measuring can have any size at all. We are measuring the intensity of the waves, or the energy in the cork, and if the waves are very quiet, if my finger is only jiggling a little, then there will be very little motion of the cork. No matter how much it is, it is proportional. It can have any size; it does not come in lumps; it is not all there or nothing.
What we are going to measure is the intensity of the waves, or, to be precise, the energy generated by the waves at a point. What happens if we measure this intensity, which I will call 'I' to remind you that it is an intensity and not a number of particles of any kind? The curve I12, that is when both holes are open, is shown in the diagram (fig. 29). It is an interesting, complicated looking curve. If we put the detector in different places we get an intensity which varies very rapidly in a peculiar manner. You are probably familiar with the reason for that. The reason is that the ripples as they come have crests and troughs spreading from hole No. 1, and they have crests and troughs spreading from hole No. 2. If we are at a place which is exactly in between the two holes, so that the two waves arrive at the same time, the crests will come on top of each other and there will be plenty of jiggling. We have a lot of jiggling right in dead centre. On the other hand if I move the detector to some point further from hole No. 2 than hole No. 1, it takes a little longer for the waves to come from 2 than from 1, and when a crest is arriving from 1 the crest has not quite reached there yet from hole 2, in fact it is a trough from 2, so that the water tries to move up and it tries to move down, from the influences of the waves coming from the two holes, and the net result is that it does not move at all, or practically not at all. So we have a low bump at that place. Then if it moves still further over we get enough delay so that crests come together from both holes, although one crest is in fact a whole wave behind, and so you get a big one again, then a small one, a big one, a small one... depending upon the way the crests and troughs 'interfere'. The word interference again is used in science in a funny way. We can have what we call constructive interference, as when both waves interfere to make the intensity stronger. The important thing is that I12 is not the same as I1 plus I2, and we say it shows constructive and destructive interference. We can find out what I1 and I2 look like by closing hole No. 2 to find I1, and closing hole No. 1 to find I2. The intensity that we get if one hole is closed is simply the waves from one hole, with no interference, and the curves are shown in fig. 2. You will notice that I1 is the same as N1, and I2 the same as N2 and yet I12 is quite different from N12.
As a matter of fact, the mathematics of the curve I12 is rather interesting. What is true is that the height of the water, which we will call h, when both holes are open is equal to the height that you would get from No. 1 open, plus the height that you would get from No. 2 open. Thus, if it is a trough the height from No. 2 is negative and cancels out the height from No. 1. You can represent it by talking about the height of the water, but it turns out that the intensity in any case, for instance when both holes are open, is not the same as the height but is proportional to the square of the height. It is because of the fact that we are dealing with squares that we get these very interesting curves.
The source is now a big mass of stuff which is being shaken up and down in the water. The armour plate becomes a long line of barges or jetties with a gap in the water in between. Perhaps it would be better to do it with ripples than with big ocean waves; it sounds more sensible. I wiggle my finger up and down to make waves, and I have a little piece of wood as a barrier with a hole for the ripples to come through. Then I have a second barrier with two holes, and finally a detector. What do I do with the detector? What the detector detects is how much the water is jiggling. For instance, I put a cork in the water and measure how it moves up and down, and what I am going to measure in fact is the energy of the agitation of the cork, which is exactly proportional to the energy carried by the waves. One other thing: the jiggling is made very regular and perfect so that the waves are all the same space from one another. One thing that is important for water waves is that the thing we are measuring can have any size at all. We are measuring the intensity of the waves, or the energy in the cork, and if the waves are very quiet, if my finger is only jiggling a little, then there will be very little motion of the cork. No matter how much it is, it is proportional. It can have any size; it does not come in lumps; it is not all there or nothing.
What we are going to measure is the intensity of the waves, or, to be precise, the energy generated by the waves at a point. What happens if we measure this intensity, which I will call 'I' to remind you that it is an intensity and not a number of particles of any kind? The curve I12, that is when both holes are open, is shown in the diagram (fig. 29). It is an interesting, complicated looking curve. If we put the detector in different places we get an intensity which varies very rapidly in a peculiar manner. You are probably familiar with the reason for that. The reason is that the ripples as they come have crests and troughs spreading from hole No. 1, and they have crests and troughs spreading from hole No. 2. If we are at a place which is exactly in between the two holes, so that the two waves arrive at the same time, the crests will come on top of each other and there will be plenty of jiggling. We have a lot of jiggling right in dead centre. On the other hand if I move the detector to some point further from hole No. 2 than hole No. 1, it takes a little longer for the waves to come from 2 than from 1, and when a crest is arriving from 1 the crest has not quite reached there yet from hole 2, in fact it is a trough from 2, so that the water tries to move up and it tries to move down, from the influences of the waves coming from the two holes, and the net result is that it does not move at all, or practically not at all. So we have a low bump at that place. Then if it moves still further over we get enough delay so that crests come together from both holes, although one crest is in fact a whole wave behind, and so you get a big one again, then a small one, a big one, a small one... depending upon the way the crests and troughs 'interfere'. The word interference again is used in science in a funny way. We can have what we call constructive interference, as when both waves interfere to make the intensity stronger. The important thing is that I12 is not the same as I1 plus I2, and we say it shows constructive and destructive interference. We can find out what I1 and I2 look like by closing hole No. 2 to find I1, and closing hole No. 1 to find I2. The intensity that we get if one hole is closed is simply the waves from one hole, with no interference, and the curves are shown in fig. 2. You will notice that I1 is the same as N1, and I2 the same as N2 and yet I12 is quite different from N12.
As a matter of fact, the mathematics of the curve I12 is rather interesting. What is true is that the height of the water, which we will call h, when both holes are open is equal to the height that you would get from No. 1 open, plus the height that you would get from No. 2 open. Thus, if it is a trough the height from No. 2 is negative and cancels out the height from No. 1. You can represent it by talking about the height of the water, but it turns out that the intensity in any case, for instance when both holes are open, is not the same as the height but is proportional to the square of the height. It is because of the fact that we are dealing with squares that we get these very interesting curves.
h12 = h1 + h2
That was water. Now we start again, this time with electrons (fig. 30).
The source is a filament, the barriers tungsten plates, these are holes in the tungsten plate, and for a detector we have any electrical system which is sufficiently sensitive to pick up the charge of an electron arriving with whatever energy the source has. If you would prefer it, we could use photons with black paper instead of the tungsten plate — in fact black paper is not very good because the fibres do not make sharp holes, so we would have to have something better — and for a detector a photo-multiplier capable of detecting the individual photons arriving. What happens with either case? I will discuss only the electron case, since the case with photons is exactly the same.
First, what we receive in the electrical detector, with a sufficiently powerful amplifier behind it, are clicks, lumps, absolute lumps. When the click comes it is a certain size, and the size is always the same. If you turn the source weaker the clicks come further apart, but it is the same sized click. If you turn it up they come so fast that they jam the amplifier. You have to turn it down enough so, that there are not too many clicks for the machinery that you are using for the detector. Next, if you put another detector in a different place and listen to both of them you will never get two clicks at the same time, at least if the source is weak enough and the precision with which you measure the time is good enough. If you cut down the intensity of the source so that the electrons come few and far between, they never give a click in both detectors at once. That means that the thing which is coming comes in lumps — it has a definite size, and it only comes to one place at a time. Right, so electrons, or photons, come in lumps. Therefore what we can do is the same thing as we did for bullets: we can measure the probability of arrival. What we do is hold the detector in various places — actually if we wanted to although it is expensive, we could put detectors all over at the same time and make the whole curve simultaneously — but we hold the detector in each place, say for an hour, and we measure at the end of the hour how many electrons came, and we average it. What do we get for the number of electrons that arrive? The same kind of N12 as with bullets? Figure 30 shows what we get for N12, that is what we get with both holes open. That is the phenomenon of nature, that she produces the curve which is the same as you would get for the interference of waves. She produces this curve for what? Not for the energy in a wave but for the probability of arrival of one of these lumps.
The mathematics is simple. You change I to N, so you have to change h to something else, which is new — it is not the height of anything — so we invent an 'a', which we call a probability amplitude, because we do not know what it means. In this case a1 is the probability amplitude to arrive from hole No. 1, and a2 the probability amplitude to arrive from hole No. 2. To get the total probability amplitude to arrive you add the two together and square it. This is a direct imitation of what happens with the waves, because we have to get the same curve out so we use the same mathematics.
I should check on one point though, about the interference. I did not say what happens if we close one of the holes. Let us try to analyse this interesting curve by presuming that the electrons came through one hole or through the other. We close one hole, and measure how many come through hole No. 1, and we get the simple curve N1. Or we can close the other hole and measure how many come through hole No. 2, and we get the N2 curve. But these two added together do not give the same as N1 + N2; it does show interference. In fact the mathematics is given by this funny formula that the probability of arrival is the square of an amplitude which itself is the sum of two pieces, N12 = (a1+ a2)2. The question is how it can come about that when the electrons go through hole No. 1 they will be distributed one way, when they go through hole No. 2 they will be distributed another way, and yet when both holes are open you do not get the sum of the two. For instance, if I hold the detector at the point q with both holes open I get practically nothing, yet if I close one of the holes I get plenty, and if I close the other hole I get something. I leave both holes open and I get nothing; I let them come through both holes and they do not come any more. Or take the point at the centre; you can show that that is higher than the sum of the two single hole curves. You might think that if you were clever enough you could argue that they have some way of going around through the holes back and forth, or they do something complicated, or one splits in half and goes through the two holes, or something similar, in order to explain this phenomenon. Nobody, however, has succeeded in producing an explanation that is satisfactory, because the mathematics in the end are so very simple, the curve is so very simple (fig. 30).
I12 ≠ I1 + I2 (Interference) I12 = (h12)2 I1 = (h1)2 I2 = (h2)2 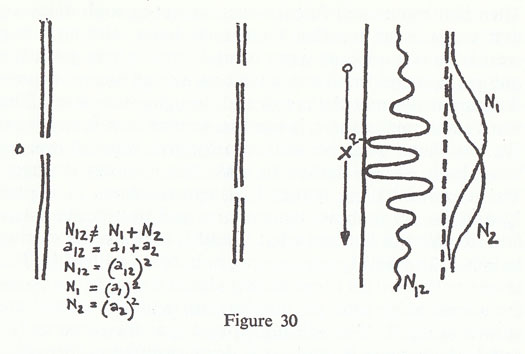
Feynman only adds to the mystery by saying a particle is both a wave and a particle. The wave is just abstract information (a theoretical and statistical prediction) about the distribution of paths and positions of particles over large numbers of experiments.
I will summarize, then, by saying that electrons arrive in lumps, like particles, but the probability of arrival of these lumps is determined as the intensity of waves would be. It is in this sense that the electron behaves sometimes like a particle and sometimes like a wave. It behaves in two different ways at the same time (fig. 31).
There is no "it" in the wave. 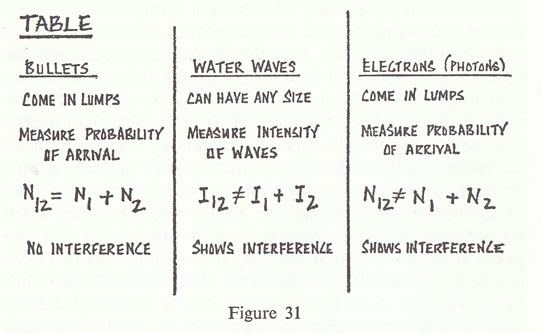 That is all there is to say. I could give a mathematical description to figure out the probability of arrival of electrons under any circumstances, and that would in principle be the end of the lecture — except that there are a number of subtleties involved in the fact that nature works this way. There are a number of peculiar things, and I would like to discuss those peculiarities because they may not be self-evident at this point.
To discuss the subtleties, we begin by discussing a proposition which we would have thought reasonable, since these things are lumps. Since what comes is always one complete lump, in this case an electron, it is obviously reasonable to assume that either an electron goes through hole No. 1 or it goes through hole No. 2. It seems very obvious that it cannot do anything else if it is a lump. I am going to discuss this proposition, so I have to give it a name; I will call it `proposition A'.
That is all there is to say. I could give a mathematical description to figure out the probability of arrival of electrons under any circumstances, and that would in principle be the end of the lecture — except that there are a number of subtleties involved in the fact that nature works this way. There are a number of peculiar things, and I would like to discuss those peculiarities because they may not be self-evident at this point.
To discuss the subtleties, we begin by discussing a proposition which we would have thought reasonable, since these things are lumps. Since what comes is always one complete lump, in this case an electron, it is obviously reasonable to assume that either an electron goes through hole No. 1 or it goes through hole No. 2. It seems very obvious that it cannot do anything else if it is a lump. I am going to discuss this proposition, so I have to give it a name; I will call it `proposition A'.
 Now we have already discussed a little what happens with proposition A. If it were true that an electron either goes through hole No. 1 or through hole No. 2, then the total number to arrive would have to be analysable as the sum of two contributions. The total number which arrive will be the number that come via hole 1, plus the number that come via hole 2. Since the resulting curve cannot be easily analysed as the sum of two pieces in such a nice manner, and since the experiments which determine how many would arrive if only one hole or the other were open do not give the result that the total is the sum of the two parts, it is obvious that we should conclude that this proposition is false.
Now we have already discussed a little what happens with proposition A. If it were true that an electron either goes through hole No. 1 or through hole No. 2, then the total number to arrive would have to be analysable as the sum of two contributions. The total number which arrive will be the number that come via hole 1, plus the number that come via hole 2. Since the resulting curve cannot be easily analysed as the sum of two pieces in such a nice manner, and since the experiments which determine how many would arrive if only one hole or the other were open do not give the result that the total is the sum of the two parts, it is obvious that we should conclude that this proposition is false.
We can show that the electron can go through just one hole and yet proposition A is not false, because Feynman has ignored something very important - the wave function that determines the probabilities of finding particles is different when both holes are open. The information that generates interference comes from the surrounding environment.
If it is not true that the electron either comes through hole No. 1 or hole No. 2, maybe it divides itself in half temporarily or something. So proposition A is false. That is logic.
Unfortunately, or otherwise, we can test logic by experiment. We have to find out whether it is true or not that the electrons come through either hole 1 or hole 2, or maybe they go round through both holes and get temporarily split up, or something.
Why interference patterns show up when both holes are open, even when particles go through just one hole, though we cannot know which hole or we lose the interference
All we have to do is watch them. And to watch them we need light. So we put behind the holes a source of very intense light. Light is scattered by electrons, bounced off them, so if the light is strong enough you can see electrons as they go by. We stand back, then, and we look to see whether when an electron is counted we see, or have seen the moment before the electron is counted, a flash behind hole 1 or a flash behind hole 2, or maybe a sort of half flash in each place at the same time. We are going to find out now how it goes, by looking. We turn on the light and look, and lo, we discover that every time there is a count at the detector we see either a flash behind No. 1 or a flash behind No. 2. What we find is that the electron comes one hundred per cent, complete, through hole 1 or through hole 2 — when we look. A paradox!
Let us squeeze nature into some kind of a difficulty here. I will show you what we are going to do. We are going to keep the light on and we are going to watch and count how
many electrons come through. We will make two columns, one for hole No. 1 and one for hole No. 2, and as each electron arrives at the detector we will note in the appropriate column which hole it came through. What does the column for hole No. 1 look like when we add it all together for different positions of the detector? If I watch behind hole No. 1 what do I see? I see the curve N1 (fig. 30). That column is distributed just as we thought when we closed hole 2, much the same way whether we are looking or not. If we close hole 2 we get the same distribution in those that arrive as if we were watching hole No. 1; likewise the number that have arrived via hole No. 2 is also a simple curve N2. Now look, the total number which arrive has to be the total number. It has to be the sum of the number N1 plus the number N2; because each one that comes through has been checked off in either column 1 or column 2. The total number which arrive absolutely has to be the sum of these two. It has to be distributed as N1 + N2. But I said it was distributed as the curve N12. No, it is distributed as N1 + N2. It really is, of course; it has to be and it is. If we mark with a prime the results when a light is lit, then we find that N1', is practically the same as N1, without the light, and N2' is almost the same as N2. But the number N12', that we see when the light is on and both holes are open is equal to the number that we see through hole 1 plus the number that we see through hole 2. This is the result that we get when the light is on. We get a different answer whether I turn on the light or not. If I have the light turned on, the distribution is the curve N1 + N2. If I turn off the light, the distribution is N12. Turn on the light and it is N1 + N2 again. So you see, nature has squeezed out! We could say, then, that the light affects the result. If the light is on you get a different answer from that when the light is off. You can say too that light affects the behaviour of electrons. If you talk about the motion of the electrons through the experiment, which is a little inaccurate, you can say that the light affects the motion, so that those which might have arrived at the maximum have somehow been deviated or kicked by the light and arrive at the minimum instead, thus smoothing the curve to produce the simple N1 + N2 curve.
Electrons are very delicate. When you are looking at a baseball and you shine a light on it, it does not make any difference, the baseball still goes the same way. But when you shine a light on an electron it knocks him about a bit, and instead of doing one thing he does another, because you have turned the light on and it is so strong. Suppose we try turning it weaker and weaker, until it is very dim, then use very careful detectors that can see very dim lights, and look with a dim light. As the light gets dimmer and dimmer you cannot expect the very very weak light to affect the electron so completely as to change the pattern a hundred per cent from N12 to N1 + N2. As the light gets weaker and weaker, somehow it should get more and more like no light at all. How then does one curve turn into another? But of course light is not like a wave of water. Light also comes in particle-like character, called photons, and as you turn down the intensity of the light you are not turning down the effect, you are turning down the number of photons that are coming out of the source. As I turn down the light I am getting fewer and fewer photons. The least I can scatter from an electron is one photon, and if I have too few photons sometimes the electron will get through when there is no photon coming by, in which case I will not see it. A very weak light, therefore, does not mean a small disturbance, it just means a few photons. The result is that with a very weak light I have to invent a third column under the title 'didn't see'. When the light is very strong there are few in there, and when the light is very weak most of them end in there. So there are three columns, hole 1, hole 2, and didn't see. You can guess what happens. The ones I do see are distributed according to the curve N1 + N2. The ones I do not see are distributed as the curve N12. As I turn the light weaker and weaker I see less and less and a greater and greater fraction are not seen. The actual curve in any case is a mixture of the two curves, so as the light gets weaker it gets more and more like N12 in a continuous fashion.
I am not able here to discuss a large number of different ways which you might suggest to find out which hole the electron went through. It always turns out, however, that it is impossible to arrange the light in any way so that you can tell through which hole the thing is going without disturbing the pattern of arrival of the electrons, without destroying the interference. Not only light, but anything else — whatever you use, in principle it is impossible to do it. You can, if you want, invent many ways to tell which hole the electron is going through, and then it turns out that it is going through one or the other. But if you try to make that instrument so that at the same time it does not disturb the motion of the electron, then what happens is that you can no longer tell which hole it goes through and you get the complicated result again.
Heisenberg noticed, when he discovered the laws of quantum mechanics, that the new laws of nature that he had discovered could only be consistent if there were some basic limitation to our experimental abilities that had not been previously recognized. In other words, you cannot experimentally be as delicate as you wish. Heisenberg proposed his uncertainty principle which, stated in terms of our own experiment, is the following. (He stated it in another way, but they are exactly equivalent, and you can get from one to the other.) 'It is impossible to design any apparatus whatsoever to determine through which hole the electron passes that will not at the same time disturb the electron enough to destroy the interference pattern'. No one has found a way around this. I am sure you are itching with inventions of methods of detecting which hole the electron went through; but if each one of them is analysed carefully you will find out that there is something the matter with it. You may think you could do it without disturbing the electron, but it turns out there is always something the matter, and you can always account for the difference in the patterns by the disturbance of the instruments used to determine through which hole the electron comes.
This is a basic characteristic of nature, and tells us something about everything. If a new particle is found tomorrow, the kaon — actually the kaon has already been found, but to give it a name let us call it that — and I use kaons to interact with electrons to determine which hole the electron is going through, I already know, ahead of time — I hope — enough about the behaviour of a new particle to say that it cannot be of such a type that I could tell through which hole the electron would go without at the same time producing a disturbance on the electron and changing the pattern from interference to no interference. The uncertainty principle can therefore be used as a general principle to guess ahead at many of the characteristics of unknown objects. They are limited in their likely character.
The Copenhagen interpretation insists we know nothing about a path when not looking (measuring). Our measurements create the path, they said. But Einstein said that goes too far. We can say, and know, things like the particle is conserving its mass, momentum, energy, spin, etc. along its path. It cannot divide in two and go through both holes!
Let us return to our proposition A — 'Electrons must go either through one hole or another'. Is it true or not? Physicists have a way of avoiding the pitfalls which exist. They make their rules of thinking as follows. If you have an apparatus which is capable of telling which hole the electron goes through (and you can have such an apparatus), then you can say that it either goes through one hole or the other. It does; it always is going through one hole or the other — when you look. But when you have no apparatus to determine through which hole the thing goes, then you cannot say that it either goes through one hole or the other. (You can always say it — provided you stop thinking immediately and make no deductions from it. Physicists prefer not to say it, rather than to stop thinking at the moment.) To conclude that it goes either through one hole or the other when you are not looking is to produce an error in prediction. That is the logical tight-rope on which we have to walk if we wish to interpret nature.
This proposition that I am talking about is general. It is not just for two holes, but is a general proposition which can be stated this way. The probability of any event in an ideal experiment — that is just an experiment in which everything is specified as well as it can be — is the square of something, which in this case I have called 'a', the probability amplitude. When an event can occur in several alternative ways, the probability amplitude, this 'a' number, is the sum of the 'a's for each of the various alternatives. If an experiment is performed which is capable of determining which alternative is taken, the probability of the event is changed; it is then the sum of the probabilities for each alternative. That is, you lose the interference.
The question now is, how does it really work ? What machinery is actually producing this thing? Nobody knows any machinery. Nobody can give you a deeper explanation of this phenomenon than I have given; that is, a description of it. They can give you a wider explanation, in the sense that they can do more examples to show how it is impossible to tell which hole the electron goes through and not at the same time destroy the interference pattern. They can give a wider class of experiments than just the two slit interference experiment. But that is just repeating the same thing to drive it in. It is not any deeper; it is only wider. The mathematics can be made more precise; you can mention that they are complex numbers instead of real numbers, and a couple of other minor points which have nothing to do with the main idea. But the deep mystery is what I have described, and no one can go any deeper today.
We can not know the path or the position of an individual particle. If we do measure it to learn its path, the experimental results change. There is no longer interference.
What we have calculated so far is the probability of arrival of an electron. The question is whether there is any way to determine where an individual electron really arrives? Of course we are not averse to using the theory of probability, that is calculating odds, when a situation is very complicated. We throw up a dice into the air, and with the various resistances, and atoms, and all the complicated business, we are perfectly willing to allow that we do not know enough details to make a definite prediction; so we calculate the odds that the thing will come this way or that way. But here what we are proposing, is it not, is that there is probability all the way back: that in the fundamental laws of physics there are odds.
Suppose that I have an experiment so set up that with the light out I get the interference situation. Then I say that even with the light on I cannot predict through which hole an electron will go. I only know that each time I look it will be one hole or the other; there is no way to predict ahead of time which hole it will be. The future, in other words, is unpredictable. It is impossible to predict in any way, from any information ahead of time, through which hole the thing will go, or which hole it will be seen behind. That means that physics has, in a way, given up, if the original purpose was — and everybody thought it was — to know enough so that given the circumstances we can predict what will happen next. Here are the circumstances: electron source, strong light source, tungsten plate with two holes: tell me, behind which hole shall I see the electron? One theory is that the reason you cannot tell through which hole you are going to see the electron is that it is determined by some very complicated things back at the source: it has internal wheels, internal gears, and so forth, to determine which hole it goes through; it is fifty-fifty probability, because, like a die, it is set at random; physics is incomplete, and if we get a complete enough physics then we shall be able to predict through which hole it goes. That is called the hidden variable theory. That theory cannot be true; it is not due to lack of detailed knowledge that we cannot make a prediction.
Feynman is wrong. We can say it went through either hole 1 or hole 2. We just cannot say which hole without destroying the interference pattern!
I said that if I did not turn on the light I should get the interference pattern. If I have a circumstance in which I get that interference pattern, then it is impossible to analyse it in terms of saying it goes through hole 1 or hole 2, because that interference curve is so simple, mathematically a completely different thing from the contribution of the two other curves as probabilities. If it had been possible for us to determine through which hole the electron was going to go if we had the light on, then whether we have the light on or off is nothing to do with it. Whatever gears there are at the source, which we observed, and which permitted us to tell whether the thing was going to go through 1 or 2, we could have observed with the light off, and therefore we could have told with the light off through which hole each electron was going to go. But if we could do this, the resulting curve would have to be represented as the sum of those that go through hole 1 and those that go through hole 2, and it is not. It must then be impossible to have any information ahead of time about which hole the electron is going to go through, whether the light is on or off, in any circumstance when the experiment is set up so that it can produce the interference with the light off. It is not our ignorance of the internal gears, of the internal complications, that makes nature appear to have probability in it. It seems to be somehow intrinsic. Someone has said it this way — 'Nature herself does not even know which way the electron is going to go'.
The same conditions do not always produce the same results. It is this quantum indeterminism that breaks the causal chain of physical determinism.
A philosopher once said 'It is necessary for the very existence of science that the same conditions always produce the same results'. Well, they do not. You set up the circumstances, with the same conditions every time, and you cannot predict behind which hole you will see the electron. Yet science goes on in spite of it — although the same conditions do not always produce the same results. That makes us unhappy, that we cannot predict exactly what will happen. Incidentally, you could think up a circumstance in which it is very dangerous and serious, and man must know, and still you cannot predict.
Sad these tragic examples scientists imagine, like Schrödinger's Cat
For instance we could cook up — we'd better not, but we could — a scheme by which we set up a photo cell, and one electron to go through, and if we see it behind hole No. 1 we set off the atomic bomb and start World War III, whereas if we see it behind hole No. 2 we make peace feelers and delay the war a little longer.
The future is unpredictable
Then the future of man would be dependent on something which no amount of science can predict. The future is unpredictable.
What is necessary 'for the very existence of science', and what the characteristics of nature are, are not to be determined by pompous preconditions, they are determined always by the material with which we work, by nature herself. We look, and we see what we find, and we cannot say ahead of time successfully what it is going to look like. The most reasonable possibilities often turn out not to be the situation. If science is to progress, what we need is the ability to experiment, honesty in reporting results — the results must be reported without somebody saying what they would like the results to have been — and finally — an important thing — the intelligence to interpret the results. An important point about this intelligence is that it should not be sure ahead of time what must be. It can be prejudiced and say 'That is very unlikely; I don't like that'. Prejudice is different from absolute certainty. I do not mean absolute prejudice — just bias. As long as you are only biased it does not make any difference, because if your bias is wrong a perpetual accumulation of experiments will perpetually annoy you until they cannot be disregarded any longer. They can only be disregarded if you are absolutely sure ahead of
time of some precondition that science has to have. In fact it is necessary for the very existence of science that minds exist which do not allow that nature must satisfy some preconceived conditions, like those of our philosopher.
See also The Distinction of Past and Future For Teachers
For Scholars
|
||||||||||