James Clerk Maxwell

(1831-1879)

Many scientists before Maxwell supported the existence of atoms and molecules, from the ancient determinists Leucippus and Democritus, to Epicurus with his atomic "swerves" that enable free will and the creation of structures in an otherwise chaotic universe, to moderns like Daniel Bernoulli in the 18th century, who argued that the pressure of a gas was the result of atoms bombarding the vessel wall, to John Waterston and John Herapath in the early 19th, whose contributions were largely forgotten, and finally to the great Rudolf Clausius, who stated the Second Law of Thermodynamics in 1850 and introduced the concept of Entropy in 1865, based on the disorderly random motions of gas particles. Clausius introduced the idea of the "mean free path" traveled by a gas particle - in a straight line - between collisions with other particles.

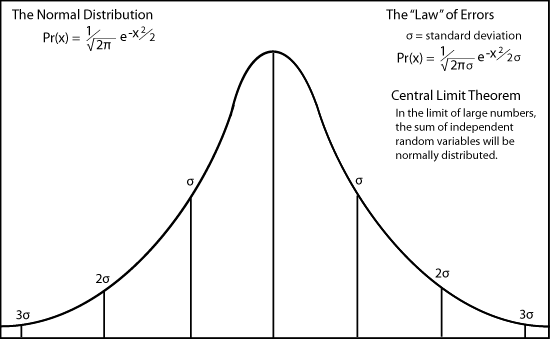
Maxwell's great contribution to the Kinetic Theory of Gases was to find the velocity distribution of the gas particles. Clausius, for simplicity, had assumed that they all move at the same speed. From simple considerations of symmetry and the assumption that motions in the y and z directions were not dependent on motions in the x direction, Maxwell showed that velocities were distributed according to the same normal distribution as the "law of errors" found in astronomical observations.

Where "normal" errors are distributed symmetrically around the mean value, the Maxwell-Boltzmann distribution of velocities decreases from the peak value as v² for low energy particles, then declines according to the exponential e^{- v²} for high energies.

The social physicist Adolphe Quételet and scientific historian Henry Thomas Buckle argued that this distribution applied to social statistics, and scholars have shown that Maxwell's derivation of his velocities distribution followed the derivation the astronomer John Herschel used to explain Quételet's work. ¹

Inspired by the dogma of mechanical determinism that seemed to have been verified by Newtonian physics, Buckle declared that statistical regularities in random human events like marriages, crimes, and suicides, proved that these events were determined and there was no room for human free will.

Maxwell's criticism of his countryman Buckle was clear.

We thus meet with a new kind of regularity — the regularity of averages — a regularity which when we are dealing with millions of millions of individuals is so unvarying that we are almost in danger of confounding it with absolute uniformity.

Maxwell comes close to asserting ontological chance, but he may only be saying one cannot derive determinism from statistical regularities
Laplace in his theory of Probability has given many examples of this kind of statistical regularity and has shown how this regularity is consistent with the utmost irregularity among the individual instances which are enumerated in making up the results. In the hands of Mr Buckle facts of the same kind were brought forward as instances of the unalterable character of natural laws. But the stability of the averages of large numbers of variable events must be carefully distinguished from that absolute uniformity of sequence according to which we suppose that every individual event is determined by its antecedents.²

(Draft Lecture on Molecules, 1784)

Ironically, many scientists and mathematicians, including Laplace himself, were such convinced determinists that they believed the statistical regularities were proof of determinism! Their thinking appears to go something like this:

Perfectly random, unpredictable individual events (like the throw of dice in games of chance) show statistical regularities that become more and more certain with more trials (the law of large numbers).
Human events show statistical regularities.
Human events are determined.

They might more reasonably have concluded that individual human events are unpredictable and random. Were they determined, they might be expected to show a non-random pattern, perhaps a signature of the Determiner.

Maxwell would have none of the argument from statistical regularity to determinism. Perhaps because his Christian religion asserted free will, he objected strenuously to the false conclusion. He said he invented his famous demon expressly to show that the Second Law of Thermodynamics has only "statistical certainty." (Letter and Papers, III, Note to Tait 'Concerning Demons,' p.186)

Maxwell asked the question in 1873, "Does the progress of Physical Science tend to given any advantage to the opinion of Necessity (or Determinism) over that of the Contingency of Events and the Freedom of the Will?" (Life of James Clerk Maxwell, p.363)

Free Will

Maxwell looked for free will in physical conditions that were poised on a knife edge of going this way or that way and which the mind could push in either direction with minimal (ideally zero) energy required.

Note that Maxwell completely understands the sensitivity to initial conditions that is the basis for today's chaos theory
When the state of things is such that an infinitely small variation of the present state will alter only by an infinitely small quantity the state at some future time, the condition of the system, whether at rest or in motion, is said to be stable; but when an infinitely small variation in the present state may bring about a finite difference in the state of the system in a finite time, the condition of the system is said to be unstable.
It is manifest that the existence of unstable conditions renders impossible the prediction of future events, if our knowledge of the present state is only approximate, and not accurate.
It has been well pointed out by Professor Balfour Stewart that physical stability is the characteristic of those systems from the contemplation of which determinists draw their arguments, and physical instability that of those living bodies, and moral instability that of those developable souls, which furnish to consciousness the conviction of free will.
Having thus pointed out some of the relations of physical science to the question, we are the better prepared to inquire what is meant by determination and what by free will.
No one, I suppose, would assign to free will a more than infinitesimal range. No leopard can change his spots, nor can any one by merely wishing it, or, as some say, willing it, introduce discontinuity into his course of existence. Our free will at the best is like that of Lucretius's atoms — which at quite uncertain times and places deviate in an uncertain manner from their course. In the course of this our mortal life we more or less frequently find ourselves on a physical or moral watershed, where an imperceptible deviation is sufficient to determine into which of two valleys we shall descend. The doctrine of free will asserts that in some such cases the Ego alone is the determining cause. The doctrine of Determinism asserts that in every case. without exception, the result is determined by the previous conditions of the subject, whether bodily or mental, and that Ego is mistaken in supposing himself in any way the cause of the actual result, as both what he is pleased to call decisions and the resultant action are corresponding events due to the same fixed laws.
(Essay on Science and Free Will, 1873)

Six years later, Maxwell was intrigued by the work of three Frenchmen, Boussinesq, Cournot, and St Venant, on singular points in the solution of hydrodynamic equations which suggested complete unpredictability of future states. These resembled Lucretius' (really Epicurus') atomic swerves, and they anticipate modern non-linear, deterministic chaos. Although Maxwell did not find the idea really satisfactory, it did challenge the metaphysics of strict causal determinism.

Maxwell wrote in a letter to Francis Galton² (who never responded to the suggestion):

There are certain cases in which a material system, when it comes to a phase in which the particular path which it is describing coincides with the envelope of all such paths may either continue in the particular path or take to the envelope (which in these cases is also a possible path) and which course it takes is not determined by the forces of the system (which are the same for both cases) but when the bifurcation of path occurs, the system, ipso facto, invokes some determining principle which is extra physical (but not extra natural) to determine which of the two paths it is to follow.
When it is on the enveloping path it may at any instant, at its own sweet will, without exerting any force or spending any energy, go off along that one of the particular paths which happens to coincide with the actual condition of the system at that instant.
I think Boussinesq's method is a very powerful one against metaphysical arguments about cause and effect

Maxwell's Demon

In his 1871 book Theory of Heat, Maxwell speculated about a being that could manipulate individual molecules of a gas and sort out the faster-moving ones from the slower ones, to create a temperature difference in apparent violation of the second law of thermodynamics:

One of the best established facts in thermodynamics is that it is impossible in a system enclosed in an envelope which permits neither change of volume nor passage of heat, and in which both the temperature and the pressure are everywhere the same, to produce any inequality of temperature or of pressure without the expenditure of work. This is the second law of thermodynamics, and it is undoubtedly true as long as we can deal with bodies only in mass, and have no power of perceiving or handling the separate molecules of which they are made up. But if we conceive a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are still as essentially finite as our own, would be able to do what is at present impossible to us. For we have seen that the molecules in a vessel full of air at uniform temperature are moving with velocities by no means uniform, though the mean velocity of any great number of them, arbitrarily selected, is almost exactly uniform. Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower ones to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics.
This is only one of the instances in which conclusions which we have drawn from our experience of bodies consisting of an immense number of molecules may be found not to be applicable to the more delicate observations and experiments which we may suppose made by one who can perceive and handle the individual molecules which we deal with only in large masses.
In dealing with masses of matter, while we do not perceive the individual molecules, we are compelled to adopt what I have described as the statistical method of calculation, and to abandon the strict dynamical method, in which we follow every motion by the calculus. Let him first observe the molecules in A and when he sees one coming the square of whose velocity is less than the mean sq. vel. of the molecules in B let him open the hole and let it go into B. Next let him watch for a molecule of B, the square of whose velocity is greater than the mean sq. vel. in A, and when it comes to the hole let him draw the slide and let it go into A, keeping the slide shut for all other molecules.

Maxwell described the being's sorting strategy in more detail in a letter:

Let him first observe the molecules in A and when he sees one coming the square of whose velocity is less than the mean sq. vel. of the molecules in B let him open the hole and let it go into B. Next let him watch for a molecule of B, the square of whose velocity is greater than the mean sq. vel. in A, and when it comes to the hole let him draw the slide and let it go into A, keeping the slide shut for all other molecules.
Then the number of molecules in A and B are the same as at first, but the energy in A is increased and that in B diminished, that is, the hot system has got hotter and the cold colder and yet no work has been done, only the intelligence of a very observant and neat-fingered being has been employed.

Maxwell emphasized that it was the intelligence of his being that did the work. His friend William Thomson (later Lord Kelvin) named the being "Maxwell's intelligent demon." Thomson said:

The definition of a demon, according to the use of this word by Maxwell, is an intelligent being endowed with free-will and fine enough tactile and perceptive organization to give him the faculty of observing and influencing individual molecules of matter.
Clerk Maxwell's 'demon' is a creature of imagination having certain, perfectly well defined powers of action, purely mechanical in their character, invented to help us to understand the 'Dissipation of Energy' in nature.
He is a being with no preternatural qualities and differs from real living animals only in extreme smallness and agility. ... He cannot create or annul energy; but just as a living animal does, he can store up limited quantities of energy, and reproduce them at will. By operating selectively on individual atoms he can reverse the natural dissipation of energy, can cause one-half of a closed jar of air, or of a bar of iron, to become glowingly hot and the other ice cold; can direct the energy of the moving molecules of a basin of water to throw the water up to a height and leave it there proportionately cooled...; can 'sort' the molecules in a solution of salt or in a mixture of two gases, so as to reverse the natural process of diffusion, and produce concentration of the solution in one portion of the water, leaving pure water in the remainder of the space occupied; or, in the other case separate the gases into different parts of the containing vessel.

Maxwell confirmed Thomson as the source of the word demon, and explained the demon's purpose.

Concerning Demons.
1. Who gave them this name? Thomson.
2. What were they by nature? Very small BUT lively beings incapable of doing work but able to open and shut valves which move without friction or inertia.
3. What was their chief end? To show that the 2nd Law of Thermodynamics has only a statistical certainty.

Six papers and two letters by Maxwell

For Teachers

To hide this material, click on the Normal link.

Noesis
Stanford Encyclopedia of Philosophy
Wikipedia

For Scholars

To hide this material, click on the Teacher or Normal link.

1. That Quételet was the source of Maxwell's idea for a normal distribution is explained by Theodore Porter, The Rise of Statistical Thinking 1820-1900, Princeton 1986), p.118. The argument depends on Maxwell's use of a mathematical argument identical to one given by John Herschel as an explanation of Quételet. It seems as likely that Herschel himself is Maxwell's inspiration. And Maxwell is quite familiar with normal distributions, probably from reading Laplace, Calcul des Probabilities."

From Draft of Lecture on Molecules 1873, Letters and Papers of JCM, vol II, 478 (pp.932-933)

We thus meet with a new kind of regularity — the regularity of averages — a regularity which when we are dealing with millions of millions of individuals is so unvarying that we are almost in danger of confounding it with absolute uniformity.
Laplace in his theory of Probability has given many examples of this kind of statistical regularity and has shown how this regularity is consistent with the utmost irregularity among the individual instances which are enumerated in making up the results. In the hands of Mr Buckle facts of the same kind were brought forward as instances of the unalterable character of natural laws. But the stability of the averages of large numbers of variable events must be carefully distinguished from that absolute uniformity of sequence according to which we suppose that every individual event is determined by its antecedents.
For instance if a quantity of air is enclosed in a vessel and left to itself we may be morally (perfectly) certain that whenever we choose to examine it we shall find the pressure uniform in horizontal strata and greater below than above, that the temperature will be uniform throughout, and that there will be no sensible currents of air in the vessel.
But there is nothing inconsistent with the laws of motion in supposing that in a particular case a very different event might occur. For instance if at a given instant a certain number of the molecules should each of them encounter one of the remaining molecules and if in each case one of the molecules after the encounter should be moving vertically upwards and if in addition the molecules above then happened not to get into the way of these upward moving molecules, — the result would be a sort of explosion by which a mass of air would be projected upwards with the velocity of a cannon ball while a larger mass would be blown downwards with an equivalent momentum. We are morally certain that such an event will not take place within the air of the vessel however long we leave it. What are the grounds of this certainty.
The explosion will certainly happen if certain conditions are satisfied. Each of these conditions by itself is not only possible but is in the common course of events as often satisfied as not. But as the number of conditions which must be satisfied at once is to be counted by millions of millions the improbability of the occurrence of all these conditions amounts to what we are unable to distinguish from an impossibility.
Nevertheless it is no more improbable that at a given instant the molecules should be arranged in one definite manner than in any other definite manner. We are as certain that the exact arrangement which the molecules have at the present instant will never again be repeated as that the arrangement which would bring about the explosion will never occur.

LETTER TO FRANCIS GALTON

26 FEBRUARY 1879

From Letters and Papers of James Clerk Maxwell, vol III, 731, p.761-3

Do you take any interest in Fixt Fate, Free Will &c. If so Boussinesq [of hydrodynamic reputation] 'Conciliation du veritable determinisme mecanique avec 1'existence de la vie et de la liberte morale' (Paris 1878) does the whole business by the theory of the singular solutions of the differential equations of motion. Two other Frenchmen have been working on the same or a similar track. Cournot (now dead)(') and de St Venant [of elastic reputation Torsion of Prisms &c].

Another, also in the engineering line of research, Philippe Breton seems to me to be somewhat like minded with these.

There are certain cases in which a material system, when it comes to a phase in which the particular path which it is describing coincides with the envelope of all such paths may either continue in the particular path or take to the envelope (which in these cases is also a possible path) and which course it takes is not determined by the forces of the system (which are the same for both cases) but when the bifurcation of path occurs, the system, ipso facto, invokes some determining principle which is extra physical (but not extra natural) to determine which of the two paths it is to follow.

When it is on the enveloping path it may at any instant, at its own sweet will, without exerting any force or spending any energy, go off along that one of the particular paths which happens to coincide with the actual condition of the system at that instant.

In most of the former methods Dr Balfour Stewarts &c there was a certain small but finite amount of travail decrochant or trigger-work for the Will to do. Boussinesq has managed to reduce this to mathematical zero, but at the expense of having to restrict certain of the arbitrary constants of the motion to mathematically definite values, and this I think will be found in the long run, very expensive.

But I think Boussinesq's method is a very powerful one against metaphysical arguments about cause and effect and much better than the insinuation that there is something loose about the laws of nature, not of sensible magnitude but enough to bring her round in time.

Yours very truly
J. CLERK MAXWELL

Chapter 1.5 - The Philosophers	Chapter 2.1 - The Problem of Knowledge
Home	Part Two - Knowledge

Normal | Teacher | Scholar