---

(Uber einen Satz der Dynamik and die mechanische Warmetheorie, Annalen der Physik 57, pp. 485-94 (1896); English trans, Stephen Brush, Kinetic Theory, vol.2, p.208) Poincaré's recurrence theorem shows that irreversible processes are impossible in a mechanical system. A simple proof of this theorem is given.

The kinetic theory cannot provide an explanation of irreversible processes unless one makes the implausible assumption that only those initial states that evolve irreversibly are actually realized in nature, while the other states, which from a mathematical viewpoint are more probable, actually do not occur. It is concluded that it is necessary to formulate either the second law of thermodynamics or the mechanical theory of heat in an essentially different way, or else give up the latter theory altogether.

In the second chapter of Poincaré's prize essay on the three-body problem,¹ there is proved a theorem from which it follows that the usual description of the thermal motion of molecules, on which is based for example the kinetic theory of gases, requires an important modification in order that it be consistent with the thermodynamic law of increase of entropy. Poincaré's theorem says that in a system of mass points under the influence of forces that depend only on position in space, in general any state of motion (characterized by configurations and velocities) must recur arbitrarily often, at least to any arbitrary degree of approximation even if not exactly, provided that the coordinates and velocities cannot increase to infinity. Hence, in such a system irreversible processes are impossible since (aside from singular initial states) no single-valued continuous function of the state variables, such as entropy, can continually increase; if there is a finite increase, then there must be a corresponding decrease when the initial state recurs. Poincaré, in the essay cited, used his theorem for astronomical discussions on the stability of sun systems; he does not seem to have noticed its applicability to systems of molecules or atoms and thus to the mechanical theory of heat.

---

(Entgegnung auf die wärmetheoretischen Betrachtungen des Hrn. E. Zermelo, Annalen der Physik 57, pp. 773-84 (1896); English trans, Stephen Brush, Kinetic Theory, vol.2, p.218) Poincaré's theorem, on which Zermelo's remarks are based, is clearly correct, but Zermelo's application of it to the theory of heat is not. The nature of the H-curve (entropy vs. time) which can be deduced from the kinetic theory is such that if an initial state deviates considerably from the Maxwell distribution, it will tend toward that distribution with enormously large probability, and during an enormously long time will deviate from it by only vanishingly small amounts. Of course if one waits long enough, the initial state will eventually recur, but the recurrence time is so long that there is no possibility of ever observing it.

In contradiction to Zermelo's statement, the singular initial states which do not approach the Maxwell distribution are very small in number compared to those that do. Consequently there is no difficulty in explaining irreversible processes by means of the kinetic theory. According to the molecular-kinetic view, the second law of thermodynamics is merely a theorem of probability theory. The fact that we never observe exceptions does not prove that the statistical viewpoint is wrong, because the theory predicts that the probability of an exception is practically zero when the number of molecules is large.

Clausius, Maxwell and others have already repeatedly mentioned that the theorems of gas theory have the character of statistical truths. I have often emphasized as clearly as possible t that Maxwell's law of the distribution of velocities among gas molecules is by no means a theorem of ordinary mechanics which can be proved from the equations of motion alone; on the contrary, it can only be proved that it has very high probability, and that for a large number of molecules all other states have by comparison such a small probability that for practical purposes they can be ignored. At the same time I have also emphasized that the second law of thermodynamics is from the molecular viewpoint merely a statistical law. Zermelo's paper² shows that my writings have been misunderstood; nevertheless it pleases me for it seems to be the first indication that these writings have been paid any attention in Germany.

Poincaré's theorem, which Zermelo explains at the beginning of his paper, is clearly correct, but his application of it to the theory of heat is not.

I have based the proof of Maxwell's velocity distribution law on the theorem that according to the laws of probability a certain quantity H (which is some kind of measure of the deviation of the prevailing state from Maxwell's) can only decrease for a stationary gas in a stationary container. The nature of this decrease will become most clear when one draws a graph (as I have done §) with time as abscissa and the corresponding values of H as ordinates, thus giving the so-called H-curve. (One may subtract off the minimum value Hmin from all values of H.) If one first sets the number of molecules equal to infinity and allows the time of the motion to become very large, then in the overwhelming majority of cases one obtains a curve which asymptotically approaches the abscissa axis. The Poincaré theorem is not applicable in this case, as can easily be seen.

However, if one takes the time of the motion to be infinite, while the number of molecules is very large but not actually infinite, then the H-curve has a different appearance. As I have already shown, it almost always runs very close to the abscissa axis. Only very rarely does it rise up above this axis; we call this a peak, and indeed the probability of a peak decreases very rapidly as the height of the peak increases. At those times when the ordinate of the H-curve is very small, Maxwell's distribution holds almost exactly; but significant deviations occur at high peaks of the H-curve. Zermelo thinks that he can conclude from Poincaré's theorem that it is only for certain singular initial states, whose number is infinitesimal compared to all possible initial states, that the Maxwell distribution will be approached, while for most initial states this law is not obeyed. This seems to me to be incorrect. It is just for certain singular initial states that the Maxwell distribution is never reached, for example when all the molecules are initially moving in a line perpendicular to two sides of the container. For the overwhelming majority of initial conditions, on the other hand, the H-curve has the character mentioned above.

If the initial state lies on an enormously high peak, i.e. if it is completely different from the Maxwellian state, then the state will approach this velocity distribution with enormously large probability, and during an enormously long time it will deviate from it by only vanishingly small amounts. Of course if one waits an even longer time, he may observe an even higher peak, and indeed the initial state will eventually recur; in a mathematical sense one must have an infinite time duration infinitely often.

Zermelo is therefore completely correct when he asserts that the motion is periodic in a mathematical sense; but, far from contradicting my theorem, this periodicity is in complete harmony with it. One should not forget that the Maxwell distribution is not a state in which each molecule has a definite position and velocity, and which is thereby attained when the position and velocity of each molecule approach these definite values asymptotically. For a finite number of molecules the Maxwell distribution can never be true exactly, but only to a high degree of approximation. It is in no way a special singular distribution which is to be contrasted to infinitely many more non-Maxwellian distributions; rather it is characterized by the fact that by far the largest number of possible velocity distributions have the characteristic properties of the Maxwell distribution, and compared to these there are only a relatively small number of possible distributions that deviate significantly from Maxwell's. Whereas Zermelo says that the number of states that finally lead to the Maxwellian state is small compared to all possible states, I assert on the contrary that by far the largest number of possible states are " Maxwellian " and that the number that deviate from the Maxwellian state is vanishingly small.

For the first molecule, any position in space, and any values of its velocity components consistent with conservation of total energy, are equally probable.

If one combines all states of all molecules, then he obtains in almost every case the Maxwell distribution, to a high degree of approximation. Only a few combinations give a completely different distribution of states.

An analogy for this is provided by the theory of the method of least squares, where one assumes that each elementary error is equally likely to have a positive or equal negative value; it is then proved that if one combines all possible values of the elementary errors in all possible ways, the great majority of combinations will obey the Gaussian law of errors, and for relatively few combinations will there be significant deviations; the deviations are not impossible, but they are very unlikely.

An even simpler example is provided by the game of dice. In 6000 throws with the same dice one might obtain 1000 one's, 1000 two's, and so forth, not because any such random sequence of throws is more probable than a series of 6000 one's, but rather because there are many more possible combinations corresponding to an equal number of one's, two's, etc., than corresponding to all one's.

The theory of probability therefore leads to the result (as is well known) that a recurrence of an initial state is not mathematically impossible, and indeed is to be expected if the time of the motion is sufficiently long, since the probability of finding a state very close to the initial state is very small but not zero. The consequence of Poincaré's theorem — that, apart from a few singular initial states, a state very close to the initial state must eventually occur after a very long time —is therefore in complete agreement with my theory.

It is only the conclusion that the mechanical viewpoint must somehow be changed or even given up that is incorrect. This conclusion would be justified only if the mechanical viewpoint led to some consequence that was in contradiction to experience. This would only be the case, however, if Zermelo could prove that the duration of the period of time after which the previous state of the gas must recur according to Poincaré's theorem has an observable length. It should indeed be obvious that if a trillion tiny spheres, each with a high velocity, are initially collected together in one corner of a container with absolutely elastic walls, then in a very short time they will be uniformly distributed throughout the container; and that the time required for all their collisions to have compensated each other in such a way that they all come back to the same corner, must be so large that no one will be present to observe it. Though it seems unnecessary, I have estimated the magnitude of this time in the appendix, and the value obtained is comfortingly large. Though this calculation makes no pretense to accuracy, it still shows that it cannot be proved from Poincaré's theorem that the theoretical existence of a recurrence time involves any contradiction with experience, since the length of this time makes any attempt to observe it ridiculous. The states that we observe all fall in the intermediate time between the beginning and end of the cycle, so that Poincaré's theorem does not exclude states that approximate with arbitrary accuracy the Maxwellian state.

Zermelo's case is therefore only one of many cases (and indeed one that does exceptionally little harm to gas theory) where a state that is theoretically only very improbable must be considered as never occuring in practice. Thus for example in oxyhydrogen gas at ordinary temperatures there must be occasional collisions of two or three molecules with very high velocities; if these were not excluded, oxyhydrogen gas would turn into water at ordinary temperatures.

To give another example, the case that during one second no molecule of a gas collides with a piston is only very improbable but not impossible.

The time that one must wait for a measurable amount of water to be produced from oxyhydrogen gas at ordinary temperature, or for the pressure on a piston to decrease by a measurable amount from its average value, is not as long as a recurrence time, but it is still sufficiently long to preclude observation. An argument against the kinetic theory can be derived from such considerations only when such phenomena fail to appear in a period of time for which calculation indicates that they should appear.

This does not seem to be the case; on the contrary, for temperatures lower than the conversion temperature, actual traces of chemical conversion can be found; likewise, it is observed that very small particles in a gas execute motions which result from the fact that the pressure on the surface of the particles may fluctuate.

Thus when Zermelo concludes, from the theoretical fact that the initial states in a gas must recur — without having calculated how long a time this will take — that the hypotheses of gas theory must be rejected or else fundamentally changed, he is just like a dice player who has calculated that the probability of a sequence of 1000 one's is not zero, and then concludes that his dice must be loaded since he has not yet observed such a sequence!

The foregoing remarks are intimately connected with my interpretation of the second law of thermodynamics in the papers cited above. According to the molecular-kinetic view, this law is merely a theorem of probability theory. According to this view, it cannot be proved from the equations of motion that all phenomena must evolve in a certain direction in time. For all phenomena where only visible motion occurs, so that the body always moves as a whole, both directions must be equivalent. On the other hand, when the motion involves a very large number of very small molecules, then there must be (aside from a small number of exceptional cases) a progression from less probable to more probable states, and therefore a continual change in a definite direction, such as, in a gas, the evolution toward a Maxwellian distribution. On the other hand, when it is a question of the motions of individual molecules, this would no longer be expected.

The first and second cases are confirmed by experience; the third case has not yet been realized. Its possibility is hence neither proved nor disproved. Famous scientists, such as Helmholtz, ¹ have believed this, and as I have tried to indicate in my book on gas theory, ² the opinion that the second law is merely a statistical law is not only not contradicted by the facts but agrees rather well with them. Gibbs ³ also arrived, by considering purely empirical facts, at the following conclusion: "The impossibility of an incompensated decrease of entropy seems to be reduced to an improbability".

We therefore arrive at the following result: if one considers heat to be molecular motion which takes place according to the general equations of mechanics, and assumes that the complexes of bodies that we observe are at present in very improbable states, then he can obtain a theorem which agrees with the second law for phenomena observed up to now.

Of course as soon as one observes bodies of such small size that they contain only a few molecules, the theorem will no longer be valid. However, since no experiments have yet been done on such small bodies, the assumption does not contradict our present experience; indeed, the experiments that have been done on small particles in gases are favourable to the assumption, although we can hardly say that we have an experimental proof of it yet.

When the bodies in question contain many molecules, there must occur very small deviations from this theorem, since the number of molecules is not infinite. But these deviations could only add up to an observable value in a very long period of time, so that this consequence of atomistics cannot be tested by experiment. This is all the more true since gas theory claims to give only an approximate description of reality. Perturbations experienced by the molecules as a result of the aether or the electrical properties of the molecules, etc., must be left out of the theory because of our complete ignorance concerning such effects. There is no such thing as an absolutely smooth wall; on the contrary, every gas is really interacting with the entire universe, and hence the validity of the kinetic theory is not destroyed by small deviations from experience.

An answer to the question — how does it happen that at present the bodies surrounding us are in a very improbable state — cannot be given, any more than one can expect science to tell us why phenomena occur at all and take place according to certain laws.

Gas theory is not to be confused with the theory of central forces — i.e. with the hypothesis that all natural phenomena can be explained by means of central forces between mass points — since gas theory does not assume that either the properties of the aether or the internal constitution of molecules can be explained by centres of force, but only that for the interaction of two molecules during a collision the Lagrange equations of motion are valid with sufficient accuracy for the explanation of thermal phenomena.

A consequence of the Poincaré theorem may still be used against the theory of central forces with respect to the properties of the entire universe. One may say that according to Poincaré's theorem the entire universe must return to its initial state after a sufficiently long time, and hence there must be times when all processes take place in the opposite direction. How shall we decide, when we leave the domain of the observable, whether the age of the universe, or the number of centres of force which it contains is infinite? Moreover, in this case the assumption that the space available for the motion, and the total energy, are finite, is questionable. The assumption of the unlimited validity of the irreversibility principle, when applied to the universe for an infinitely long period of time, leads (as is well known) to the scarcely more attractive consequence that, when all irreversible processes have been played out, the universe will continue to exist without any events, or all events will gradually disappear. Just as it would be wrong to deduce from this the incorrectness of the irreversibility principle, so it would also be wrong to suppose that it proves anything against atomistics.

All the paradoxes raised against the mechanical viewpoint are therefore meaningless and based on errors. However, if the difficulties offered by the clear comprehension of gas-theoretic theorems cannot be overcome, then we should in fact follow the suggestion of Zermelo and decide to give up the theory entirely.

We assume a container of volume 1 cc. In this container there will be about a trillion ( = n) molecules of air at ordinary density. The velocity of each molecule will initially be 500 metres per second. The average distance between the centres of two neighbouring molecules is about 10^-6 cm.

We now construct around the midpoint of each molecule a cube of edge-length 10^-7 cm, which we call the initial space of the molecule in question. We also construct a velocity diagram by representing the velocity of each molecule by a line from the origin with the appropriate magnitude and direction. The end-point of this line is called the velocity point of the molecule. Here we divide the entire infinite space into cubes of 1 metre edge length, which we call the elementary cubes. The elementary cube in which the velocity point of a molecule is found initially will be called the initial space of its velocity point.

We now ask after how long a time, according to Poincaré's theorem, will the centres and velocity points of all the molecules return simultaneously to their initial spaces? Note that we do not require exact recurrence, since we accept the velocity state of a molecule as being the same as its initial state if its velocity components return to values that differ by no more than 1 metre from their original values.

We assume that each molecule experiences 4.10⁹ collisions per second. It then follows that there will be in all about b = 2.10²⁷ collisions per second in the gas. In such a collision, the velocity points of two molecules will generally be displaced to different elementary cubes. According to Poincaré's theorem the original state does not have to recur until the velocity points have gone through all possible combinations of the elementary cubes.

The first molecule can have all possible velocities from zero up to (500.10⁹ = a) m/sec. If it has velocity v₁ m/sec, then the second can have all possible velocities from zero up to √(a² + v₁²) m/sec, and so forth.

The number of possible combinations of all the velocity points in the different elementary cubes is therefore:

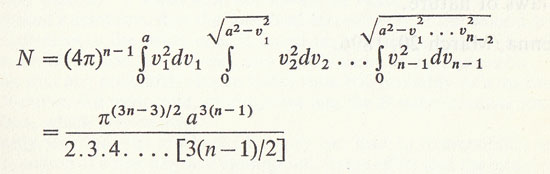or

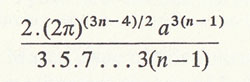according as n is odd or even.

Since each of these combinations lasts on the average 1/b seconds, all of them will be gone through in N/b seconds. After this time all molecules except one must have come back to their original velocity state. The velocity direction of this last molecule is not restricted, nor is the position of the centre of any of the molecules. In order to make the state the same as the original one, the midpoint of each molecule must also return to its initial space, so that the above number must again be multipled by another number of similar magnitude.

Though the number N/b is enormous, one can obtain some idea of its magnitude by noting that it has many trillions of digits. For comparison, suppose that every star visible with the best telescope has as many planets as does the sun, and on each planet live as many men as are on the earth, and each of these men lives a trillion years; then the total number of seconds that they all live will still have less than 50 digits.

If the gas molecules were initially distributed uniformly throughout the container, and all of them had the same velocity, then after only a hundred-millionth of a second they would already have nearly a Maxwellian velocity distribution. Comparison of these numbers shows, on the one hand, how small a fraction of the total number of possible state distributions is made up of those that deviate noticeably from the Maxwell distribution; and on the other hand, how certain are such theorems that theoretically are merely probability laws but in practice have the same significance as laws of nature.

Vienna, March 20, 1896.

---

(Ueber mechanische Erklärungen irreversibler Vorgänge, Annalen der Physik 59, 793-801 (1896).; English trans, Stephen Brush, Kinetic Theory, vol.2, p.229) Boltzmann has conceded that the commonly accepted version of the second law of thermodynamics is incompatible with the mechanical viewpoint. Whereas the author holds that the former, a principle that summarizes an abundance of established experimental facts, is more reliable than a mathematical theorem based on unverifiable hypotheses, Boltzmann wishes to preserve the mechanical viewpoint by changing the second law into a "mere probability theorem", which need not always be valid.

Boltzmann's assertion, that the statistical formulation of the second law is really equivalent to the usual one, is based on postulated properties of the H-curve which he has not proved, and which seem to be impossible. His argument that any arbitrarily chosen initial state will probably be a maximum on the H-curve, if it were valid, would prove that the H-curve consists entirely of maxima, which is nonsense.

The only way that the mechanical theory can lead to irreversibility is by the introduction of a new physical assumption, to the effect that the initial state always corresponds to a point at or just past the maximum on the H-curve; but this would be assuming what was supposed to be proved.

---

(Zu Hrn. Zermelo's Abhandlung Ober die mechanische Erklärung irreversibler Vorgange, Annalen der Physik 60, pp. 392-8 (1897); English trans, Stephen Brush, Kinetic Theory, vol.2, p.238) The second law of thermodynamics can be proved from the mechanical theory if one assumes that the present state of the universe, or at least that part which surrounds us, started to evolve from an improbable state and is still in a relatively improbable state. This is a reasonable assumption to make, since it enables us to explain the facts of experience, and one should not expect to be able to deduce it from anything more fundamental.

The applicability of probability theory to physical situations, which is disputed by Zermelo, cannot by rigorously proved, but the fact that one never observes those events that theoretically should be quite rare is certainly not a valid argument against the theory.

One may speculate that the universe as a whole is in thermal equilibrium and therefore dead, but there will be local deviations from equilibrium which may last for the relatively short time of a few eons. For the universe as a whole, there is no distinction between the "backwards" and "forwards" directions of time, but for the worlds on which living beings exist, and which are therefore in relatively improbable states, the direction of time will be determined by the direction of increasing entropy, proceeding from less to more probable states.

I will be as brief as possible without loss of clarity.

§1. The second law will be explained mechanically by means of assumption A (which is of course unprovable) that the universe, considered as a mechanical system — or at least a very large part of it which surrounds us — started from a very improbable state, and is still in an improbable state. Hence, if one takes a smaller system of bodies in the state in which he actually finds them, and suddenly isolates this system from the rest of the world, then the system will initially be in an improbable state, and as long as the system remains isolated it will always proceed toward more probable states. On the other hand, there is a very small probability that the enclosed system is initially in thermal equilibrium, and that while it remains enclosed it moves far enough away from equilibrium that its entropy decrease is noticeable.

The question is not what will be the behaviour of a completely arbitrary system, but rather what will happen to a system existing in the present state of the world. The initial state precedes the later states, so that Zermelo's conclusion that all points of the H-curve must be maxima is invalid. Hence, it turns out that entropy always increases, temperature and concentration differences are always equalized, that the initial value of H is such that during the time of observation it almost always decreases, and that initial and final states are not interchangeable, in contradiction to Zermelo's assertions. Assumption A is a comprehensible physical explanation of the peculiarity of the initial state, consistent with the laws of mechanics; or better, it is a unified viewpoint corresponding to these laws, which allows one to predict the type of peculiarity of the initial state in any special case; for one can never expect that the explanatory principle must itself be explained.

On the other hand, if we do not make any assumption about the present state of the universe, then of course we cannot expect to find that a system isolated from the universe, whose initial state is completely arbitrary, will be in an improbable state initially rather than later. On the contrary it is to be expected that at the moment of separation the system will be in thermal equilibrium. In the few cases where this does not happen, it will almost always be found that if the state of the isolated system is followed either backwards or forwards in time, it will almost immediately pass to a more probable state. Much rarer will be the cases in which the state becomes still more improbable as time goes on; but such cases will be just as frequent as those where the state becomes more improbable as one follows it backwards in time.

§2. The applicability of probability theory to a particular case cannot of course be proved rigorously. If, out of 100,000 objects of a certain kind, about 100 are annually destroyed by fire, then we cannot be sure that this will happen next year. On the contrary, if the same conditions could be maintained for 10¹⁰¹⁰ years, then during this time it would often happen that all 100,000 objects would burn up on the same day; and likewise there will be entire years during which not a single object is damaged. Despite this, every insurance company relies on probability theory.

It is even more valid, on account of the huge number of molecules in a cubic millimetre, to adopt the assumption (which cannot be proved mathematically for any particular case) that when two gases of different kinds or at different temperatures are brought in contact, each molecule will have all the possible different states corresponding to the laws of probability and determined by the average values at the place in question, during a long period of time. These probability arguments cannot replace a direct analysis of the motion of each molecule; yet if one starts with a variety of initial conditions, all corresponding to the same average values (and therefore equivalent from the viewpoint of observation), one is entitled to expect that the results of both methods will agree, aside from some individual exceptions which will be even rarer than in the above example of 100,000 objects all burning on the same day. The assumption that these rare cases are not observed in nature is not strictly provable (nor is the entire mechanical picture itself) but in view of what has been said it is so natural and obvious, and so much in agreement with all experience with probabilities, from the method of least squares to the dice game, that any doubt on this point certainly cannot put in question the validity of the theory when it is otherwise so useful.

It is completely incomprehensible to me how anyone can see a refutation of the applicability of probability theory in the fact that some other argument shows that exceptions must occur now and then over a period of eons of time; for probability theory itself teaches just the same thing.

§3. Let us imagine that a partition which separates two spaces filled with different kinds of gas is suddenly removed. One could hardly find another situation (at least one in which the method of least squares is applicable) where there are so many independent causes acting in such different ways, and in which the application of probability theory is so amply justified. The opinion that the laws of probability are not valid here, and that in most cases the molecules do not diffuse, but instead a large part of the container has significantly more nitrogen, and another part has significantly more oxygen, cannot be disproved, even if I were to calculate exactly the motions of trillions of molecules in millions of different special cases. Nevertheless this opinion certainly does not have enough justification to cast doubt on the usefulness of a theory that starts from the assumption of the applicability of probability theory and draws the logical consequence from this assumption.

Poincare's theorem does not contradict the applicability of probability theory but rather supports it, since it shows that in eons of time there will occur a relatively short period during which the state probability and the entropy of the gas will significantly decrease, and that a more ordered state similar to the initial state will occur. During the enormously long period of time before this happens, any noticeable deviation of the entropy from its maximum value is of course very improbable; however, a momentary increase or decrease of entropy is equally probable.

It is also clear from this example that the process goes on irreversibly during observable times, since one intentionally starts from a very improbable state. In the case of natural processes this is explained by the assumption that one isolates the system of bodies from the universe which is at that time in a very improbable state as a whole.

This example of two initially unmixed gases gives us incidentally a possible way of imagining the initial state of the world. For if in the example we isolate the gas found in a smaller space soon after the beginning of the diffusion from the rest of the gas, we will have the asymmetry with respect to forward and backward steps in time as in the isolated system of bodies mentioned in §1.

§4. I myself have repeatedly warned against placing too much confidence in the extension of our thought pictures beyond the domain of experience, and I am aware that one must consider the form of mechanics, and especially the representation of the smallest particles of bodies as mass-points, to be only provisionally established. With all these reservations, it is still possible for those who wish to give in to their natural impulses to make up a special picture of the universe.

One has the choice of two kinds of pictures. One can assume that the entire universe finds itself at present in a very improbable state. However, one may suppose that the eons during which this improbable state lasts, and the distance from here to Sirius, are minute compared to the age and size of the universe. There must then be in the universe, which is in thermal equilibrium as a whole and therefore dead, here and there relatively small regions of the size of our galaxy (which we call worlds), which during the relatively short time of eons deviate significantly from thermal equilibrium. Among these worlds the state probability increases as often as it decreases. For the universe as a whole the two directions of time are indistinguishable, just as in space there is no up or down. However, just as at a certain place on the earth's surface we can call "down" the direction toward the centre of the earth, so a living being that finds itself in such a world at a certain period of time can define the time direction as going from less probable to more probable states (the former will be the "past" and the latter the "future") and by virtue of this definition he will find that this small region, isolated from the rest of the universe, is "initially" always in an improbable state. This viewpoint seems to me to be the only way in which one can understand the validity of the second law and the heat death of each individual world without invoking an unidirectional change of the entire universe from a definite initial state to a final state. The objection that it is uneconomical and hence senseless to imagine such a large part of the universe as being dead in order to explain why a small part is living — this objection I consider invalid. I remember only too well a person who absolutely refused to believe that the sun could be 20 million miles from the earth, on the grounds that it is inconceivable that there could be so much space filled only with aether and so little with life.

§5. Whether one wishes to indulge in such speculations is of course a matter of taste. It is not a question of choosing as a matter of taste between the Carnot-Clausius principle and the mechanical theory. The importance of the former, as the simplest expression of the facts so far observed, is not in dispute. I assert only that the mechanical picture agrees with it in all actual observations. That it suggests the possibility of certain new observations—for example, of the motion of small particles in liquids and gases, and of viscosity and heat conduction in very rarefied gases, etc. — and that it does not agree with the Carnot-Clausius principle on some unobservable questions (for example the behaviour of the universe or a completely enclosed system during an infinite period of time), may be called a difference in principle, if you like. In any case it provides no basis for giving up the mechanical theory, as Herr Zermelo would like to do, if it cannot be changed in principle (which one should not expect). It is precisely this difference that seems to me to indicate that the universality of our thought-pictures will be improved by studying not only the consequences of the principle in the Carnot-Clausius version but also in the mechanical version.

§6. I have always measured the probability of a state, independently of its temporal duration, by the " extension γ" (as Zermelo calls it) of its corresponding region, and I used the Liouville theorem in this connection 30 years ago. ³ The Maxwellian state is simply the most probable because it can be realized in the largest number of ways. The total extension y of the region of all those states for which the velocity distribution is approximately given by the Maxwell distribution is therefore much greater than the total extension of the regions of all other states. It was only to illustrate the relation between the temporal course of the states and their probabilities that I represented the reciprocal value of this probability for the different successive states by the H-curve, in the case of a large finite number of hard gas molecules.

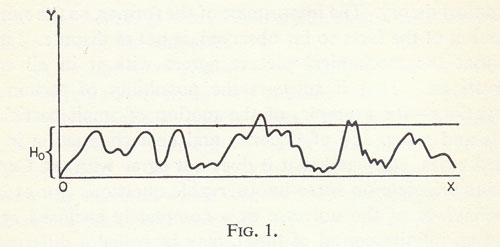Aside from a vanishingly small number of special initial states, the most probable states will also occur the most frequently (at least for a very large number of molecules). The ordinates of this curve are almost always very small, and these small ordinates are of course not usually maxima. It is only the ordinates with unusually large values that are mostly maxima, and indeed they are more likely to be maxima the greater they are. The fact that a very large ordinate H₀ is more often a maximum than the intersection of the line y = H₀ with a still higher peak is a consequence of the enormous increase in rarity of peaks with increasing height. See the above figure, which is of course to be taken with a pinch of salt. A correct figure could not be printed because the H-curve actually has a large number of maxima and minima within each finite segment, and cannot be represented by a line with continuously changing direction. It would be better to call it an aggregate of many points very close together, or small horizontal segments.⁴

The Poincaré theorem is of course inapplicable to a terrestrial body which we can observe, since such a body is not completely isolated; likewise, it is inapplicable to the completely isolated gas treated by the kinetic theory, if one first lets the number of molecules become infinite, and then the quotient of the time between successive collisions and the time of observation.

Vienna, 16 December 1896.

---

See also Response to Loschmidt.