There are presently several "interpretations" of quantum mechanics. Many, perhaps most, are attempts to eliminate the element of chance or indeterminism that is involved in the so-called collapse of the wave function.

The Information Interpretation is simply "standard quantum physics" plus information being recorded irreversibly. Unlike the Copenhagen Interpretation, we offer several visualizations of what is going on in quantum reality,

The Information Interpretation is based on three simple premises:

• Quantum systems evolve in two ways:
  • the first is the wave function deterministically exploring all the possibilities for interaction,

  • the second is the particle randomly choosing one of those possibilities to become actual.

• No knowledge can be gained by a "conscious observer" unless new information has already been irreversibly recorded in the universe. That information can be created and recorded in either the target quantum system or the measuring apparatus. Only then can it become knowledge in the observer's mind.

• In our two-stage model of free will, an agent first freely generates alternative possibilities, then evaluates them and chooses one, adequately determined by its motives, reasons, desires, etc. First come "free alternatives," then "willed actions." Just as with quantum processes - first possibilities, then actuality.
  The measuring apparatus is quantal, not deterministic or "classical." It need only be statistically determined and capable of recording the irreversible information about an interaction. The human mind is similarly only statistically determined.

Information physics claims there is only one world, the quantum world, and the "quantum to classical transition" occurs for any large macroscopic object that contains a large number of atoms. For large enough systems, independent quantum events are "averaged over." The uncertainty in position and momentum of the object becomes less than the observational uncertainty
Δv Δx ≥ h / m goes to zero as h / m goes to zero.

The classical laws of motion, with their implicit determinism and strict causality, emerge when objects are large enough so that microscopic events can be ignored, but this determinism is fundamentally statistical and causes are only probabilistic, however near to certainty.

Information philosophy interprets the wave function ψ as a "possibilities" function. With this simple change in terminology, the mysterious process of a wave function "collapsing" becomes more understandable. The wave function ψ evolves to explore all the possibilities (with mathematically calculable probabilities). When a single actuality is realized, the probability for all the non-actualized possibilities goes to zero ("collapses") instantaneously.

But they could never reconcile the macroscopic irreversibility needed for the second law

Information physics is standard quantum physics. It accepts the Schrödinger equation of motion, the principle of superposition, the axiom of measurement (now including the actual information "bits" measured), and - most important - the projection postulate of standard quantum mechanics (the "collapse" that so many interpretations deny).

The "conscious observer" of the Copenhagen Interpretation is not required for a projection, for the wave-function to "collapse", for one of the possibilities to become an actuality. What the collapse does require is an interaction between systems that creates information that is irreversible and observable, though not necessarily observed.

Among the founders of quantum mechanics, almost everyone agreed that irreversibility is a key requirement for a measurement. Irreversibility introduces thermodynamics into a proper formulation of quantum mechanics, and this is a key element of our information interpretation.

But this requirement was never reconciled with classical statistical mechanics, which says that collisions between material particles are reversible. Even quantum statistical mechanics claims collisions are reversible because the Schrödinger equation is time reversible. Note that Maxwell's equations of electromagnetic radiation are also time reversible.

We have shown that it is the interaction of light and matter, both on their own time reversible, that is the origin of irreversibility.

Classical interactions between large macroscopic bodies do not generate new information. Newton's laws of motion imply that the information in any configuration of bodies, motions, and force is enough to know all past and future configurations. Classical mechanics conserves information.

In the absence of interactions, an isolated quantum system evolves according to the unitary Schrödinger equation of motion. Just like classical systems, the deterministic Schrödinger equation conserves information. And just like classical systems, Schrödinger's unitary evolution is time reversible.

Unlike classical systems however, when there is an interaction between material quantum systems, the two systems become entangled and there may be a change of state in either or both systems. This change of state may create new information. Or if there is an interaction between light and matter the evolution is no longer unitary, there is an irreversible collapse of the wave function.

If that information is instantly destroyed, as in most interactions, it may never be observed macroscopically. If, on the other hand, the information is stabilized for some length of time, it may be seen by an observer and considered to be a "measurement." But it need not be seen by anyone to become new information in the universe. The universe is its own observer!
Compare Schrödinger's Cat as its own observer.

For the information (negative entropy) to be stabilized, the second law of thermodynamics requires that an amount of positive entropy greater than the negative entropy must be transferred away from the new information structure.

Exactly how the universe allows pockets of negative entropy to form as "information structures" we describe as the "cosmic creation process." This core two-step process has been going on since the origin of the universe. It continues today as we add information to the sum of human knowledge.

What then are the possibilities for new quantum states? The transformation theory of Dirac and Jordan lets us represent ψ in a set of basis functions for which the combination of quantum systems (one may be a measurement apparatus) has eigenvalues (the axiom of measurement). We represent ψ as in a linear combination (the principle of superposition) of those "possible" eigenfunctions. Quantum mechanics lets us calculate the probabilities of each of those "possibilities."

Interaction with the measurement apparatus (or indeed interaction with any other system) may select out (the projection postulate) one of those possibilities as an actuality. But for this event to be an "observable" (a John Bell "beable"), information must be created and positive entropy must be transferred away from the new information structure, in accordance with our two-stage information creation process.

All interpretations of quantum mechanics predict the same experimental results.
Information physics is no exception, because the experimental data from quantum experiments is the most accurate in the history of science.

Where interpretations differ is in the picture (the visualization) they provide of what is "really" going on in the microscopic world - the so-called "quantum reality." The "orthodox" Copenhagen interpretation of Neils Bohr and Werner Heisenberg discourages such attempts to understand the nature of the "quantum world," because they say that all our experience is derived from the "classical world" and should be described in ordinary language. This is why Bohr and Heisenberg insisted on the path and the "cut" between the quantum event and the mind of an observer.

The information interpretation encourages visualization. Schrödinger called it Anschaulichkeit. He and Einstein were right that we should be able to picture quantum reality. But that demands that we accept the reality of quantum possibilities and discontinuous random "quantum jumps," something many modern interpretations do not do. (See our visualization of the two-slit experiment, our EPR experiment visualizations, and Dirac's three polarizers to visualize the superposition of states and the projection or "collapse" of a wave function.)

Bohr was of course right that classical physics plays an essential role. His Correspondence Principle allowed him to recover some important physical constants by assuming that the discontinuous quantum jumps for low quantum numbers (low "orbits" in his old quantum theory model) converged in the limit of large quantum numbers to the continuous radiation emission and absorption of classical electromagnetic theory.

In addition, we know that in macroscopic bodies with enormous numbers of quantum particles, quantum effects are averaged over, so that the uncertainty in position and momentum of a large body still obeys Heisenberg's indeterminacy principle, but the uncertainty is for all practical purposes unmeasurable and the body can be treated classically. We can say that the quantum description of matter also converges to a classical description in the limit of large numbers of quantum particles. We call this "adequate" or statistical determinism. It is the apparent determinism we find behind Newton's laws of motion for macroscopic objects. The statistics of averaging over many independent quantum events then produces the "quantum to classical transition" for the same reason as the "law of large numbers" in probability theory.

Both Bohr and Heisenberg suggested that just as relativistic effects can be ignored when the velocity is small compared to the velocity of light (v / c → 0), so quantum effects might be ignorable when Planck's quantum of action h → 0. But this is quite wrong, because h is a constant that never goes to zero. In the information interpretation, it is always a quantum world. The conditions needed for ignoring quantum indeterminacy are when the mass of the macroscopic "classical" object is large.

Noting that the momentum p is the product of mass and velocity mv, Heisenberg's indeterminacy principle, Δp Δx > h, can be rewritten as Δv Δx > h / m. It is thus not when h is small, but when h / m is small enough, that errors in the position and momentum of macroscopic objects become smaller that can be measured.

The creation of irreversible new information also marks the transition between the quantum world and the "adequately deterministic" classical world, because the information structure itself must be large enough (and stable enough) to be seen. The typical measurement apparatus is macroscopic, so the quantum of action h becomes small compared to the mass m and h / m approaches zero.

The information interpretation thus explains why quantum superpositions like Schrödinger's Cat are not seen in the macroscopic world. Stable new information structures in the dying cat reduce the quantum possibilities (and their potential interference effects) to a classical actuality. Upon opening the box and finding a dead cat, an autopsy will reveal that the time of death was observed/recorded. The cat is its own observer.

The central element in quantum physics is the "wave function" ψ, with its mysterious wave-particle dual nature (sometimes a wave, sometimes a particle, etc.). We believe that teaching and understanding quantum mechanics would be much simpler if we called ψ the "possibilities function." It only looks like a wave in simple cases of low-dimensional coordinate space. But it always tells us the possibilities - the possible values of any observable, for example.

Given the "possibilities function" ψ, quantum mechanics allows us to calculate the "probabilities" for each of the "possibilities." The calculation depends on the free choice of the experimenter as to which "observables" to look for. If the measurement apparatus can register n discrete values, ψ can be expanded in terms of a set of basis functions (eigenfunctions) appropriate for the chosen observable, say φ_n. The expansion is

When the absolute squares of the coefficients c_n are appropriately normalized to add up to 1, the probability P_n of observing an eigenvalue n is

These probabilities are confirmed statistically by repeated identical experiments that collect large numbers of results. Quantum mechanics is the most accurate physical theory in science, with measurements accurate to thirteen decimal places.

In each individual experiment, generally just one of the possibilities becomes an actuality (some experiments leave the quantum system in a new superposition of multiple possibilities).

In our information interpretation, a possibility is realized or actualized at the moment when information is created about the new state of the system. This new information requires that positive entropy be carried away from the local increase in negative entropy.

Note that an "observer" would not be able to make a "measurement" unless there is new information to be "observed." Information must be (and is in all modern experimental systems) created and recorded before any observer looks at the results.

An information approach can help philosophers to think more clearly about quantum physics. Instead of getting trapped in talk about mysterious "collapses of the wave function," "reductions of the wave packet," or the "projection postulate" (all important issues), the information interpretation proposes we simply say that one of the "possibilities" has become "actual." It is intuitively obvious that when one possibility becomes actual, all the others are annihilated, consigned to "nothingness," as Jean-Paul Sartre put it. And because the other possibilities may have been extremely "distant" from the actuality, their instantanteous disappearances looked to Einstein to violate his principle of relativity, but they do not.

Quantum theory lets us put quantitative values on the "probabilities" for each of the "possibilities." But this means that quantum theory is fundamentally statistical, meaning indeterministic and "random." It is not a question of our being ignorant about what is going on (an epistemological problem). What's happening is ontological chance, as Einstein first showed, but as he forever disliked.

We can describe the "possibilities function" ψ as moving through space (at the speed of light, or even faster, as Einstein feared?), exploring all the possibilities for wherever the particle might be found. This too may be seen as a special kind of information. In the famous "two-slit experiment," the "possibilities function" travels everywhere, meaning that it passes through both slits, interfering with itself and thus changing the possibilities where the particle might be found. Metaphorically, it "knows" when both slits are open, even if our intuitive classical view imagines that the particle must go through only one. This changes the probabilities associated with each of the possibilities.

It is of the deepest philosophical significance that information theory is based on the mathematics of probability. If all outcomes were certain, there would be no "surprises" in the universe. Information would be conserved and a universal constant, as some mathematicians mistakenly believe. Information philosophy requires the ontological uncertainty and probabilistic outcomes of modern quantum physics to produce new information.

In Claude Shannon's theory of the communication of information, there must be multiple possible messages in order for information to be communicated. If there is but one possible message, there is no uncertainty, and no information can be communicated.

In a universe describable by the classical Newtonian laws of motion, all the information needed to produce the next moment is contained in the positions, motions, and forces on the material particles.

In a quantum world describable by the unitary evolution of the deterministic Schrödinger equation, nothing new ever happens, there is no new "outcome." Outcomes are added to standard quantum mechanics by the addition of the "projection postulate" or "collapse of the wave function" when the quantum system interacts with another system.

Information is constant in a deterministic universe. There is "nothing new under the sun." The creation of new information is not possible without the random chance and uncertainty of quantum mechanics, plus the extraordinary temporal stability of quantum mechanical structures needed to store information once it is created.

Without the extraordinary stability of quantized information structures over cosmological time scales, life and the universe we know would not be possible. That stability is the consequence of an underlying digital nature. Quantum mechanics reveals the architecture of the universe to be discrete rather than continuous, to be digital rather than analog. Digital information transfers are essentially perfect. All analog transfers are "lossy."

It is Bohr's "correspondence principle" of quantum mechanics for large quantum numbers and the "law of large numbers" of statistics which ensure that macroscopic objects can normally average out microscopic uncertainties and probabilities to provide the statistical or "adequate" determinism that shows up in all our "Laws of Nature."

We conclude, contrary to the views of Bohr and Heisenberg, that there is no need for a separate classical world. The classical laws of nature emerge statistically from quantum laws. Quantum laws, which are therefore universally applicable, converge in these two limits of large numbers to classical laws. There is no "transition" from the quantum world to a separate classical world. There is just one world, where quantum physics applies universally, but its mysterious properties, like interference, entanglement, and nonlocality, are normally invisible, averaged over, in the macroscopic world.

The problem for an informational interpretation of quantum mechanics is to explain exactly how these two convergences (large numbers of particles and large quantum numbers) allow continuous and apparently deterministic macroscopic information structures to emerge from the indeterministic and discontinuous microscopic quantum world.

We must show how the determinism in the macroscopic world is only a statistical determinism or adequate determinism that results from "averaging over" the large number of independent quantum events happening in a macroscopic object. And even more important, we must show how the occasional magnification or amplification of microscopic quantum events leads to new macroscopic information that makes human beings the "authors of their lives", that makes them "co-creators of our universe," and that guarantees a genuinely open future with alternative possibilities, not in inaccessible "parallel universes" but in the one universe that we have.

In Richard Feynman's "path integral" formulation of quantum mechanics, we may have a way to help visualize our "possibilities" function.

Feynman proposed to reformulate quantum mechanics based on just three postulates:

1. The probability for an event is given by the squared modulus of a complex number called the "probability amplitude," just as with the Heisenberg and Schrödinger pictures.

2. The probability amplitude is given by adding together the contributions of all paths in configuration space, where paths include not only the most direct from the initial state, but also paths with arbitrary curves that can go arbitrarily far away and then come back to the final state, paths so long that they imply traversal at supraluminal speeds!

3. The contribution of a path is proportional to e^{i S / ℏ}, where S is the action given by the time integral of the Lagrangian along the path.

The overall probability amplitude for a given process is the sum of the contributions over the space of all possible paths of the system in between the initial and final states. All probability amplitudes have equal weight but have varying phase of the complex action. Rapidly varying phase may significantly reduce the contribution along a path and paths may interfere with neighboring paths.

The path integrals are described as the "sum of histories" of all paths through an infinite space–time. Local quantum field theory might restrict paths to lie within a finite causally closed region, with time-like separations inside a light-cone.

A Feynman diagram is a graphical representation of one path's contribution to the probability amplitude.

Feynman's path integral method gives the same results as quantum mechanics for Hamiltonians quadratic in the momentum. Feynman's amplitudes also obey the Schrödinger equation for the Hamiltonian corresponding to the action S.

How do we interpret this as visualizing the "possibilities" in our information interpretation? We can compare the individual paths to the "virtual photons" that mediate the electromagnetic field in quantum field theory. The picture is then that an infinite number of virtual photons explore all the possibilities in the given situation. Large numbers of them go through both slits for example, and interfere with one another, preventing even a single real photon from landing on a null point in the interference pattern.

Information physics explores the quantum mechanical and thermodynamic properties of cosmic information structures, especially those that were created before the existence of human observers.

A key parameter is the amount of information per particle. When particles combine, the information per particle increases. Starting with quarks forming nucleons, nuclei combining with electrons to form atoms, atoms combining into molecules, macromolecules, crystal lattices, and other solid state structures, at every stage of growth two things are happening.

Binding energy is being transferred away from the new composite structure, carrying away positive entropy. This positive entropy more than balances the negative entropy (or information) in the new structure, thus satisfying the second law of thermodynamics. But the important thing is the increasing information per particle, which allows the new information structure to approach classical behavior.

Individual particles are no longer acting alone. Acting in concert allows them to average over quantum noise. They acquire new properties and capabilities that emerge from the component particles and are not reducible to the parts. Quantum noise destroys coherent actions of the lower-level parts of the new structure, preventing the lower level from exerting "botton-up" control. Information in the higher-level structure allows the composite system to generate new behaviors that can exercise downward causal control. Some of these behaviors depend for their successful operation on the disruptive noise in the lower level.

For example, a ribosome, assembling a polypeptide chain into a protein, depends on the chaotic and random motions of the transfer RNA molecules with amino acids attached to rapidly provide the next codon match.

To understand information creation, information physics provides new insights into the puzzling "problem of measurement" and the mysterious "collapse of the wave function" in quantum mechanics.

Information physics also probes deeply into the second law of thermodynamics to establish the irreversible increase of entropy on a quantum mechanical basis.

"Information physics" provides a new "interpretation" of quantum mechanics. But it is is not an attempt to alter the basic assumptions of standard quantum mechanics, extending them to include "hidden variables," for example. It does reject the unfortunate idea that nothing happens to quantum systems without the intervention of an "observer."

1) The Wave Function.

The central element in quantum physics is the "wave function" ψ, with its mysterious wave-particle dual nature (sometimes a wave, sometimes a particle, etc.). We believe that teaching and understanding quantum mechanics would be much simpler if we called ψ the "possibilities function." It only looks like a wave in simple cases of configuration space. But it always tells us the possibilities - the possible values of any observable, for example.

2. The Superposition Principle (and transformation theory).

Given the "possibilities function" ψ, quantum mechanics allows us to calculate the "probabilities" for each of the "possibilities." The calculation will depend on the free choice of the experimenter as to which "observables" to look for, by designing an appropriate measurement apparatus. For example, if the measurement apparatus can register n discrete values, ψ can be expanded in terms of a set of n basis functions appropriate for the chosen observable, say φ_n. The expansion is then

and we say the system is in a "superposition" of these n states.

When the absolute squares of the coefficients c_n are appropriately normalized to add up to 1, the probability P_n of observing value n is

These probabilities are confirmed statistically by repeated identical experiments that collect large numbers of results. Quantum mechanics is the most accurate physical theory in science, with measurements accurate to thirteen decimal places.

2. The Equation of Motion.

The "possibilities function" ψ evolves in time according to the unitary Schrödinger equation of motion.

where H is the Hamiltonian.

3. The Projection Postulate ("Collapse" of the Wave Function).

4. The Axiom of Measurement (impossible without information creation).

In each individual experiment, generally just one of the possibilities becomes an actuality (some experiments leave the quantum system in a new superposition of multiple possibilities).

In our information interpretation, a possibility is realized or actualized when information is created about the new state of the system. This new information requires that more positive entropy be carried away than the local increase in negative entropy.

Note that an "observer" would not be able to make a "measurement" unless there is new information to be "observed." Information can be (and usually is) created and recorded before any observer looks at the results.

An information approach can help philosophers to think more clearly about quantum physics. Instead of getting trapped in talk about mysterious "collapses of the wave function," "reductions of the wave packet," or the "projection postulate" (all important issues), the information interpretation proposes we simply say that one of the "possibilities" has become "actual." It is intuitively obvious that when one possibility becomes actual, all the others are annihilated, consigned to "nothingness," as Jean Paul-Sartre put it.

We can also say that quantum theory lets us put quantitative values on the "probabilities" for each of the "possibilities." But this means that quantum theory is statistical, meaning indeterministic and "random. It is not a question of our being ignorant about what is going on (an epistemological problem). What's happening is ontological chance.

We can also say that the "possibilities function" ψ moves through space (at the speed of light , or even faster?), exploring all the possibilities for where the particle might be found. This too may be seen as a special kind of (potential?) information. In the famous "two-slit experiment," the "possibilities function" travels everywhere, meaning that it passes through both slits, interfering with itself and thus changing the possibilities where the particle might be found. Metaphorically, it "knows" when both slits are open, even if our intuitive classical view imagines the particle to go through only one slit. This changes the probabilities associated with each of the possibilities.

Information physics accepts the principle of superposition (that arbitrary quantum states can be represented as linear combinations of system eigenstates) and the projection postulate (that interactions between quantum systems can project the two system states - or "collapse" them - into eigenstates of the separate systems or the combined entangled system).

But we replace the Copenhagen axiom of "measurement" (as involving a "measurer" or "observer") by considering instead the increased information that can sometimes occur when systems interact. If this increased information is recorded for long enough to be seen by an observer, then we can call it a measurement. The appearance of a particle at a particular spot on a photographic plate, the firing of a Geiger counter recording a particle event, or a ribosome adding an amino acid to a polypeptide chain may all be considered to be "measurements."

Just as the traditional axiom of measurement says that measurements of observables (quantities that commute with the Hamiltonian) can only yield eigenvalues, information physics accepts that the quantities of information added correspond to these eigenvalues.

What these measurements (or simply interactions without "measurements") have in common is the appearance of a microscopic particle in a particular "observable" state. But whether or not "observed," quantum particles are always interacting with other particles, and some of these interactions increase the per-particle information as the particles build up information structures.

In classical mechanics, the material universe is thought to be made up of tiny particles whose motions are completely determined by forces that act between the particles, forces such as gravitation, electromagnetic attractions and repulsions, nuclear and weak forces, etc.

The equations that describe those motions, Newton's laws of motion, were for many centuries thought to be perfect and sufficient to predict the future of any mechanical system. They provided support for many philosophical ideas about determinism.

In quantum mechanics, Newton's laws of motion, especially in the Hamiltonian formulation of those laws, are replaced by Erwin Schrodinger's wave equation, which describes the time evolution of a probability amplitude wave ψ_a,

where H is the Hamiltonian.

The probability amplitude looks like a wave and the Schrödinger equation is a wave equation. But the wave is an abstract quantity whose absolute square is interpreted as the probability of finding a quantum particle somewhere. It is distinctly not the particle itself, whose exact position is unknowable while the quantum system is evolving deterministically. It is the probability amplitude wave that interferes with itself. Particles, as such, never interfere (although they may collide). And while probabilities can be distributed throughout space, some here, some there, parts of a particle are never found. It is the whole quantum particle that is always found.

Information is conserved (a constant of the motion) during the unitary and deterministic time evolution of the wave function according to the Schrödinger equation. Information can only be created (or destroyed) during an interaction between quantum systems. It is because the system goes from a superposition of states to one of the possible states that the information changes. In what Wolfgang Pauli called a "measurement of the second kind," a system prepared in an eigenstate will, when measured again, be found with certainty, in the same state. There is no information gained in this case.

In the information interpretation of quantum mechanics, the time evolution of the wave function is not interpreted as a motion of the particle. What is evolving, what is moving, is the probability, more fundamentally, the possibilities, of finding the particle in different places, or the expectation value of various physical quantities as a function of the time.

There is no logical contradiction in the use of the deterministic Schrödinger wave equation to predict values of the (indeterministic) probability amplitude wave functions at future times. The Schrödinger equation is a universal equation (and quantum mechanics is universally true), but there is no universal wave function. Each wave function is particular to specific quantum systems, sometimes to just a single particle. And when a particle is actually found, the potential (probability) of finding it elsewhere simply vanishes instantaneously.

As Max Born put it, the equations of motion for the probability waves are deterministic and continuous, but the motion of a particle itself is indeterministic, discontinuous, and probabilistic.

John von Neumann was bothered by the fact that the projection postulate or wave-function collapse (his Process 1) was not a formal part of quantum mechanics. Dozens, if not hundreds, of physicists have attempted to produce a formal theory to describe the collapse process and make it predictable. But this is to misunderstand the irreducible chance nature of the wave-function collapse.

Long before Werner Heisenberg formulated his indeterminacy principle, it was Albert Einstein who discovered the fundamental acausal and discontinuous nature of quantum mechanics. He postulated "light quanta" in 1905, more than twenty years before quantum mechanics was developed. And in 1916, his explanation of light emission and absorption by atoms showed that the process is essentially a chance process. All attempts to predict a random process are denials of the indeterministic nature of the quantum world.

Such efforts often assume that probability itself can be understood as epistemic, the consequence of human ignorance about underlying, as yet undiscovered, deterministic laws. Historically, both scientists and philosophers have had what William James called an "antipathy to chance."

The information interpretation says that if deterministic underlying laws existed, there would be no new information creation. There would be only one possible future. But we know that the universe has been creating new information from the time of the Big Bang. Information physics adds this cosmological information creation to Einstein's discovery of microscopic quantum chance to give us a consistent picture of a quantum world that appears adequately determined at the macroscopic level. But why then did Einstein object all his life to the indeterminism ("God does not play dice," etc.) that was his own fundamental discovery?

In classical electrodynamics, electromagnetic radiation (light, radio) is known to have wave properties such as interference. When the crest of one wave in the electromagnetic field meets the trough of another, the two waves cancel one another. This field is a ponderable object. A disturbance of the field at one place is propagated to other parts of the field at the velocity of light. Einstein's gravitational field in general relativity is similar. Matter moving at one point produces changes in the field which propagate to other parts of space, again at the velocity of light, in order to be relativistically invariant.

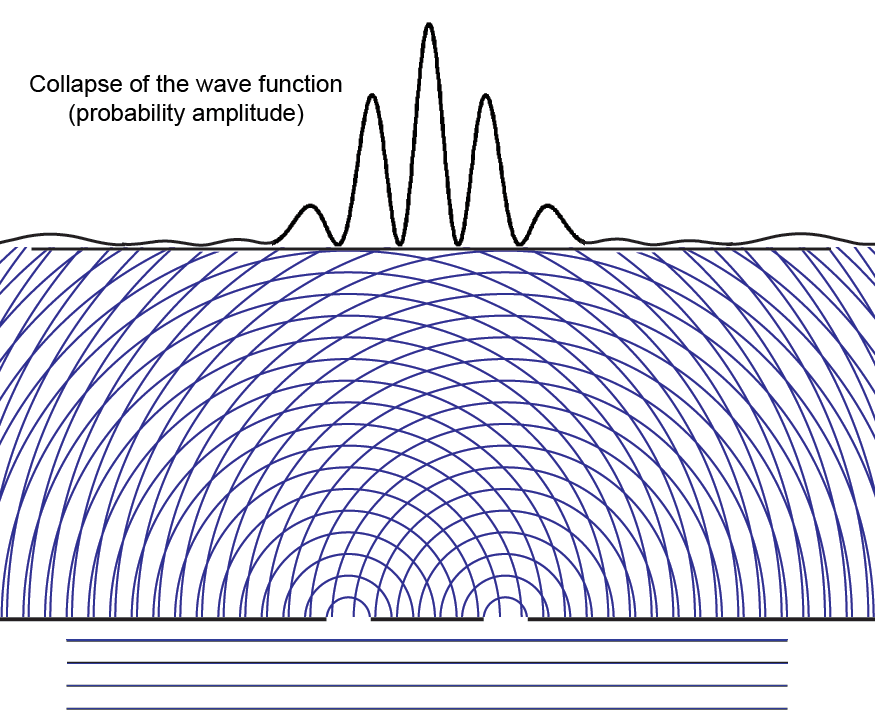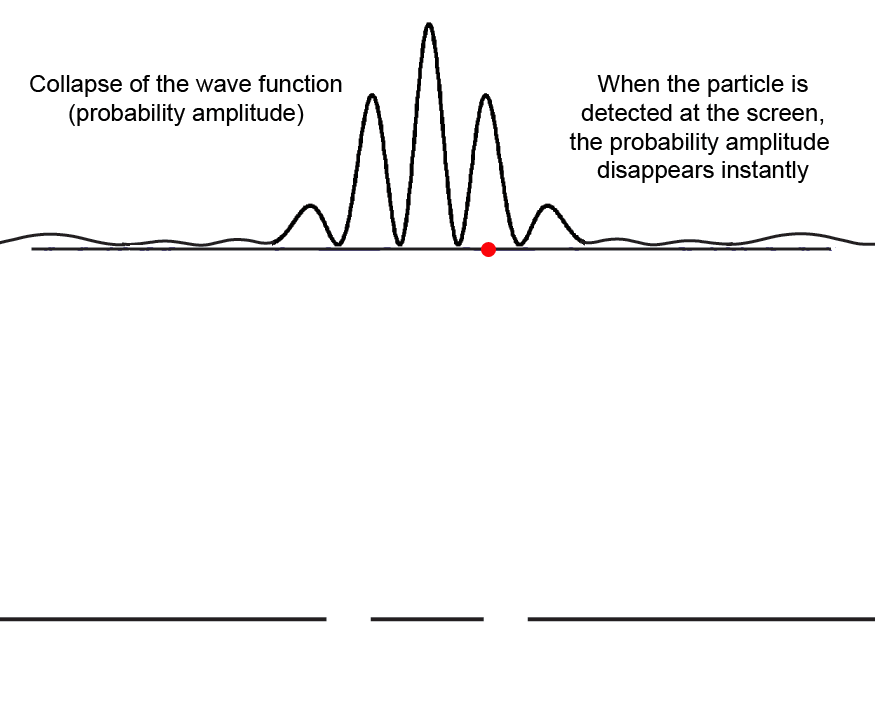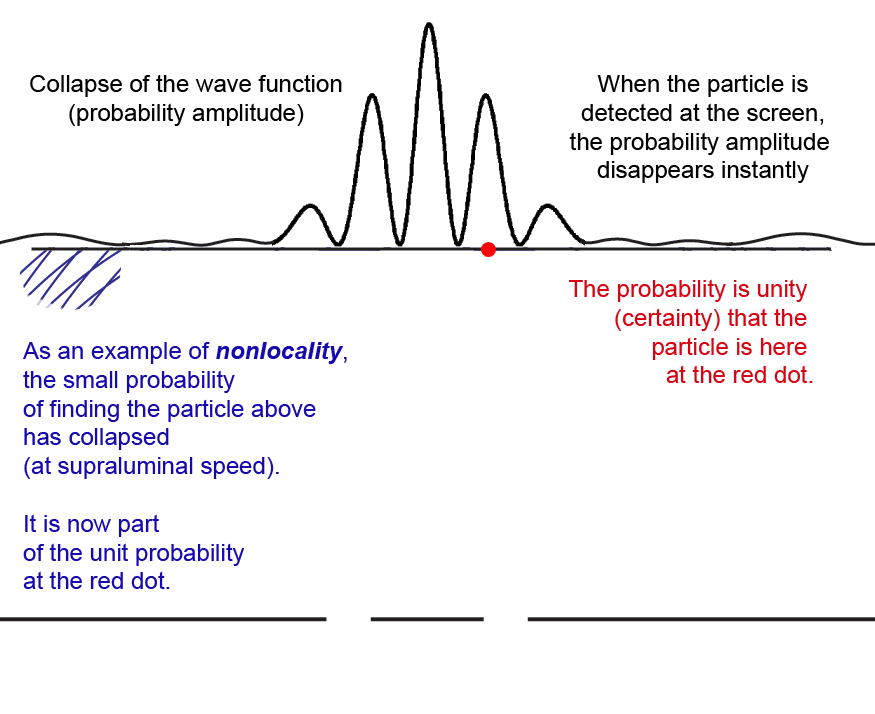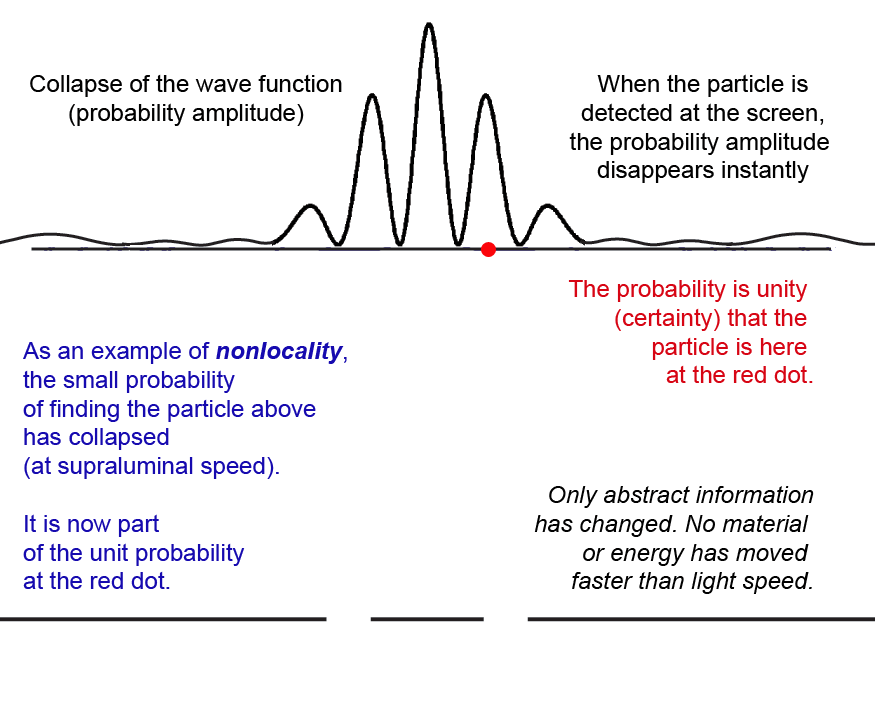
The probability amplitude wave function ψ of quantum mechanics is not such a field, however. Although Einstein sometimes referred to it as a "ghost field," and Louis de Broglie later developed a "pilot wave" theory in which waves guide the motion of material particles along paths perpendicular to the wave fronts, the wave function ψ has no ponderable substance. When a particle is detected at a given point, the probability of its being found elsewhere goes immediately to zero. Probability does not propagate at some speed to other places, reducing the probability of the particle subsequently being found there. Once located, the particle cannot be elsewhere. And that is instantaneously true.

Einstein, who spent his life searching for a "unified field theory," found this very hard to accept. He thought that instantaneous changes in the "ghost field" must violate his special theory of relativity by traveling faster than the speed of light. He described this as "nonlocal reality," the idea that something at one point (the probability of finding a particle there) could move to be somewhere else faster than light speed.

In our information interpretation, nothing that is material or energy is transferred when the probability "collapses," it is only immaterial information that changes instantly.

Animation of a probability amplitude wave function ψ collapsing - click to restart

Whereas the abstract probability amplitude moves continuously and deterministically throughout space, the concrete particle, for all we know, may move discontinuously and indeterministically to a particular point in space.

In 1900, Max Planck made the assumption that radiation is produced by resonant oscillators whose energy is quantized and proportional to the frequency of radiation ν.

For Planck, the proportionality constant h is a "quantum of action," a heuristic mathematical device that allowed him to apply Ludwig Boltzmann's work on the statistical mechanics and kinetic theory of gases to the radiation field. (Boltzmann had shown in the 1870's that the increase in entropy (the second law) could be explained if gases were made up of enormous numbers of particles his H-Theorem).

Planck applied Boltzmann's statistics of many particles to radiation and derived the distribution of radiation at different frequencies (or wavelengths) just as James Clerk Maxwell and Boltzmann had derived the distribution of velocities (or energies) of the gas particles.

Note the mathematical similarity of Planck's radiation distribution law (photons) and the Maxwell-Boltzmann velocity distribution (molecules). Both curves have a power law increase on one side to a maximum and an exponential decrease on the other side of the maximum. The molecular velocity curves cross one another because the total number of molecules is the same. With increasing temperature T, the number of photons increases at all wavelengths.

But Planck did not actually believe that radiation came in discrete particles, at least until a dozen years later. In the meantime, Albert Einstein's 1905 paper on the photoelectric effect showed that light came in discrete particles he called "light quanta," subsequently called "photons," by analogy to electrons.

Planck was not happy about the idea of light particles, because his use of Boltzmann's statistics implied that chance was real. Boltzmann himself had qualms about the reality of chance. Although Einstein also did not like the idea of chancy statistics, he did believe that energy came in packages of discrete "quanta." It was Einstein, not Planck, who quantized mechanics and electrodynamics. Nevertheless, it was for the introduction of the quantum of action h that Planck was awarded the Nobel prize in 1918.

Meanwhile, in 1916, after completing his work on the general theory of relativity, Einstein returned to thinking about a quantum theory for the interaction of radiation and matter (N.B., ten years before quantum mechanics).

In 1924, Louis de Broglie argued that if photons, with their known wavelike properties, could be described as particles, electrons as particles might show wavelike properties with a wavelength λ inversely proportional to their momentum p = m_ev.

Experiments confirmed de Broglie's assumption and led Erwin Schrödinger to derive a "wave equation" to describe the motion of de Broglie's waves. Schrödinger's equation replaces the classical Newton equations of motion.

Note that Schrödinger's equation describes the motion of only the wave aspect, not the particle aspect, and as such it implies interference. Note also that the Schrödinger equation is as fully deterministic an equation of motion as Newton's equations.

Schrödinger attempted to interpret his "wave function" for the electron as a probability density for electrical charge, but charge density would be positive everywhere and unable to interfere with itself.

Max Born shocked the world of physics by suggesting that the absolute values of the wave function ψ squared (|ψ|²) could be interpreted as the probability of finding the electron in various position and momentum states - if a measurement is made. This allows the probability amplitude ψ to interfere with itself, producing highly non-intuitive phenomena such as the two-slit experiment.

Despite the probability amplitude going through two slits and interfering with itself, experimenters never find parts of electrons. They always are found whole.

In 1932 John von Neumann explained that two fundamentally different processes are going on in quantum mechanics.

1. A non-causal process, in which the measured electron winds up randomly in one of the possible physical states (eigenstates) of the measuring apparatus plus electron.

   The probability for each eigenstate is given by the square of the coefficients c_n of the expansion of the original system state (wave function ψ) in an infinite set of wave functions φ that represent the eigenfunctions of the measuring apparatus plus electron.

   c_n = < φ_n | ψ >

   This is as close as we get to a description of the motion of the particle aspect of a quantum system. According to von Neumann, the particle simply shows up somewhere as a result of a measurement. Information physics says it shows up whenever a new stable information structure is created.

2. A causal process, in which the electron wave function ψ evolves deterministically according to Schrödinger's equation of motion for the wavelike aspect. This evolution describes the motion of the probability amplitude wave ψ between measurements.
   (ih/2π) ∂ψ/∂t = Hψ

Von Neumann claimed there is another major difference between these two processes. Process 1 is thermodynamically irreversible. Process 2 is reversible. This confirms the fundamental connection between quantum mechanics and thermodynamics that is explainable by information physics.

Information physics establishes that process 1 may create information. Process 2 is information preserving.

Physicists calculate the deterministic evolution of the Schrödinger wave function in time as systems interact or collide. At some point, they make the ad hoc assumption that the wave function "collapses." This produces a set of probabilities of finding the resulting combined system in its various eigenstates.

Although the collapse appears to be a random and ad hoc addition to the deterministic formalism of the Schrödinger equation, It is very important to note that the experimental accuracy of quantum mechanical predictions is unparalleled in physics, providing the ultimate justification for this theoretical kluge.

Moreover, without wave functions collapsing, no new information can come into the universe. Nothing unpredicatable would ever emerge. Determinism is "information-preserving." All the information we have today would have to have already existed in the original fireball.

The irreducibly random process of wave function "collapse," when one of the possibilities becomes an actuality in a quantum measurement, is not a part of the mathematical formalism describing the time evolution of the wave function (the perfectly deterministic Schrödinger equation of motion).

Collapse is an ad hoc addition to the theory, a heuristic description that enables a method of calculation to predict the probabilities of what will happen when an observer makes a measurement. The ad hoc nature of this "collapse" of the wave-function (or the "reduction" of the wave-packet) is the original problem of measurement.

Decoherence theorists today describe the problem of measurement as the absence of macroscopic superpositions of states, for example, the famous Schrödinger's Cat. Our information interpretation clarifies both of these "measurement problems."

Many physicists (especially those who, following Albert Einstein and Erwin Schrödinger, would prefer a deterministic theory) think that the collapse should be included in the formalism, to make it a predictable part of quantum theory.

Ironically, it was Einstein, many years before Heisenberg's 1927 announcement of his "uncertainty principle," who found that electromagnetic radiation is not continuous and deterministic, but discontinuous, discrete, indeterministic, and acausal. He found it a "weakness in the theory," but quantum events like the emission of a photon or decay of a radioactive nucleus happen by chance (Zufall).

We cannot say exactly when, or where, or in which direction a particle will go. We can only give statistical probabilities for such events. This Einstein was first to see and understand, but it was something he could never accept as the complete picture of quantum reality. Both he and Schrödinger (even Max Planck) denied the reality of the quantum and "quantum jumps."

In many standard discussions of quantum mechanics, and most every popular treatment, it is said that we need the consciousness of a physicist to collapse the wave function. Eugene Wigner and John Wheeler sometimes describe the observer as making up the "mind of the universe."

Von Neumann contributed a lot to this confusion by claiming that the location of the Heisenberg "cut" (Schnitt) between the microscopic system and macroscopic measurement can be put anywhere, including inside an observer's brain or mind.

The information interpretation of quantum mechanics removes the observer from the moment of the Heisenberg-von Neumann "cut." This cut is when information is created about the interaction of the quantum system with another system (which may be a measurement apparatus).

And the moment that irreversible information enters the universe is the moment of the transition from the quantum world to the classical world that the decoherence theories attempt to explain. An "observable" information structure (with mass m) has reduced the probability amplitudes to probabilities. Interference between the different possibilities disappears. The fundamental particles are still quantum, but averages over them cancel out and indeterminacy in their positions and velocities Δx Δv approaches zero as h / m approaches zero.

Measurement requires the interaction of something macroscopic, assumed to be large and adequately determined. In physics experiments, this is the observing apparatus. But in general, measurement does not require a conscious observer. It does require information creation or there will be nothing to observe.

In our discussion of Schrödinger's Cat, the cat can be its own observer.

The second law of thermodynamics says that the entropy (or disorder) of a closed physical system increases until it reaches a maximum, the state of thermodynamic equilibrium. It requires that the entropy of the universe is now and has always been increasing. (The first law is that energy is conserved.)

This established fact of increasing entropy has led many scientists and philosophers to assume that the universe we have is running down. They think that means the universe began in a very high state of information, since the second law requires that any organization or order is susceptible to decay. The information that remains today, in their view, has always been here. This fits nicely with the idea of a deterministic universe. There is nothing new under the sun. Physical determinism is "information-preserving."

But the universe is not a closed system. It is in a dynamic state of expansion that is moving away from thermodynamic equilibrium faster than entropic processes can keep up. The maximum possible entropy is increasing much faster than the actual increase in entropy. The difference between the maximum possible entropy and the actual entropy is potential information.

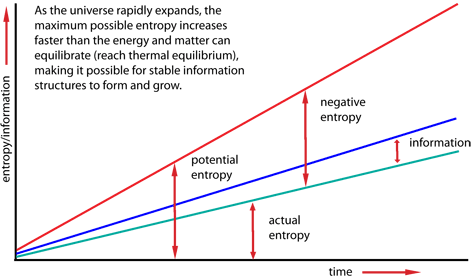
Creation of information structures means that in parts of the universe the local entropy is actually going down. Reduction of entropy locally is always accompanied by radiation of entropy away from the local structures to distant parts of the universe, into the night sky for example. Since the total entropy in the universe always increases, the amount of entropy radiated away always exceeds (often by many times) the local reduction in entropy, which mathematically equals the increase in information.