Wave-Particle Duality
Can something possibly be, at one and the same time, both a discrete particle (Werner Heisenberg) and a continuous wave (Erwin Schrödinger)?
This mystery at the heart of quantum mechanics was seen first by Albert Einstein in his 1905 paper (for which he won the Nobel Prize) proposing his "light-quantum hypothesis."
He wrote in 1905:
On the modern quantum view, what spreads out is a wave of probability amplitude, the possibilities for absorbing a whole photon somewhere.
In accordance with the assumption to be considered here, the energy of a light ray spreading
out from a point source is not continuously
distributed over an increasing space but consists
of a finite number of energy quanta which are
localized at points in space, which move without
dividing, and which can only be produced and
absorbed as whole units.
In 1909, Einstein speculated about the connection between wave and particle views:
This is wave-particle duality fourteen years before Louis deBroglie's matter waves and Erwin Schrödinger's wave equation and wave mechanics
When light was shown to exhibit interference and diffraction, it seemed almost certain that light should be considered a wave...A large body of facts shows undeniably that light has certain fundamental properties that are better explained by Newton's emission theory of light than by the oscillation theory. For this reason, I believe that the next phase in the development of theoretical physics will bring us a theory of light that can be considered a fusion of the oscillation and emission theories...
Even without delving deeply into theory, one notices that our theory of light cannot explain certain fundamental properties of phenomena associated with light. Why does the color of light, and not its intensity, determine whether a certain photochemical reaction occurs? Why is light of short wavelength generally more effective chemically than light of longer wavelength? Why is the speed of photoelectrically produced cathode rays independent of the light's intensity? Why are higher temperatures (and, thus, higher molecular energies) required to add a short-wavelength component to the radiation emitted by an object?
The fundamental property of the oscillation theory that engenders these difficulties seems to me the following. In the kinetic theory of molecules, for every process in which only a few elementary particles participate (e.g., molecular collisions), the inverse process also exists. But that is not the case for the elementary processes of radiation.
Einstein's view since 1905 was that light quanta are emitted in particular directions. There are no outgoing spherical waves (except probability amplitude waves). Even less likely are incoming spherical waves.
According to our prevailing theory, an oscillating ion generates a spherical wave that propagates outwards. The inverse process does not exist as an elementary process. A converging spherical wave is mathematically possible, to be sure; but to approach its realization requires a vast number of emitting entities. The elementary process of emission is not invertible. In this, I believe, our oscillation theory does not hit the mark. Newton's emission theory of light seems to contain more truth with respect to this point than the oscillation theory since, first of all, the energy given to a light particle is not scattered over infinite space, but remains available for an elementary process of absorption.
Dueling Wave and Particle Theories
Not only do we have the problem of understanding wave-particle duality in a quantum system, we have a full-blown wave mechanical theory (deBroglie and Schrödinger) versus a particle mechanics theory (Heisenberg, Max Born, Pascual Jordan).
Before either of these theories was developed in the mid-1920's, Einstein in 1916 showed how both wave-like and particle-like behaviors are seen in light quanta, and that the emission of light is done at random times and in random directions. This was the introduction of ontological chance (Zufall) into physics, over a decade before Heisenberg announced that quantum mechanics is acausal in his "uncertainty principle" paper of 1927.
As late as 1917, Einstein felt very much alone in believing the reality (his emphasis) of light quanta:
I do not doubt anymore the reality of radiation quanta, although I still stand quite alone in this conviction
(Letter to Besso, quoted by Abraham Pais," "Subtle is the Lord...", p.411)
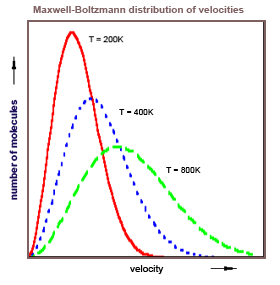
Einstein in 1916 had just derived his A and B coefficients describing the absorption, spontaneous emission, and (his newly predicted) stimulated emission of radiation. In two papers, "Emission and Absorption of Radiation in Quantum Theory," and "On the Quantum Theory of Radiation," he derived the Planck law (for Planck it was mostly a guess at the formula), he derived Planck's postulate E = hν, and he derived Bohr's second postulate Em - En = hν. Einstein did this by exploiting the obvious relationship between the Maxwell-Boltzmann distribution of gas particle velocities and the distribution of radiation in Planck's law.

The formal similarity between the chromatic distribution curve for
thermal radiation and the Maxwell velocity-distribution law is too
striking to have remained hidden for long. In fact, it was this similarity
which led W. Wien, some time ago, to an extension of the radiation
formula in his important theoretical paper, in which he derived his
displacement law...Not long ago I discovered a derivation of Planck's formula which
was closely related to Wien's original argument and which was based
on the fundamental assumption of quantum theory. This derivation
displays the relationship between Maxwell's curve and the chromatic
distribution curve and deserves attention not only because of its
simplicity, but especially because it seems to throw some light on the
mechanism of emission and absorption of radiation by matter, a
process which is still obscure to us.
But the introduction of Maxwell-Boltzmann statistical mechanical thinking to electromagnetic theory has produced what Einstein called a "weakness in the theory." It introduces the reality of an irreducible objective chance!
If light quanta are particles with energy E = hν traveling at the velocity of light c, then they should have a momentum p = E/c = hν/c. When light is absorbed by material particles, this momentum will clearly be transferred to the particle. But when light is emitted by an atom or molecule, a problem appears.
The "statistical interpretation" of
Max Born tells us the outgoing wave is the probability amplitude wave function
Ψ, whose absolute square is the
probability of finding a light particle in an arbitrary direction.
Does the molecule receive an impulse when it absorbs or emits the energy ε? For example, let us look at emission from the point of view of classical electrodynamics. When a body emits the
radiation ε it suffers a recoil (momentum) ε/c if the entire amount of radiation energy
is emitted in the same direction. If, however, the emission is a spatially symmetric
process, e.g., a spherical wave, no recoil at all occurs. This alternative also plays a
role in the quantum theory of radiation. When a molecule absorbs or emits the energy
ε in the form of radiation during the transition between quantum theoretically possible
states, then this elementary process can be viewed either as a completely or partially
directed one in space, or also as a symmetrical (nondirected) one. It turns out that we
arrive at a theory that is free of contradictions, only if we interpret those elementary
processes as completely directed processes.
An outgoing light particle must impart momentum hν/c to the atom or molecule, but the direction of the momentum can not be predicted! Neither can the theory predict the time when the light quantum will be emitted.
Such a random time was not unknown to physics. When Ernest Rutherford derived the law for radioactive decay of unstable atomic nuclei in 1900, he could only give the probability of decay time. Einstein saw the connection with radiation emission:
It speaks in favor of the theory that the statistical law assumed for [spontaneous] emission is nothing but the Rutherford law of radioactive decay.
(Pais," "Subtle is the Lord...", p.411)
But the inability to predict both the time and direction of light particle emissions, said Einstein in 1917, is "a weakness in the theory..., that it leaves time and direction of elementary processes to chance (Zufall, ibid.)." It is only a weakness for Einstein, of course, because his God does not play dice.
Einstein clearly saw, as none of his contemporaries did, that since spontaneous emission is a statistical process, it cannot possibly be described with classical physics.
The properties of elementary processes required...make it seem almost inevitable to formulate a truly quantized theory of radiation.
(Pais, ibid.)
How Einstein Discovered Wave-Particle Duality
Einstein was bothered by Planck's discovery of the blackbody radiation law. He said that it "rests on a seemingly monstrous assumption."
Planck's theory leads to the following conjecture. If it is really true that a radiative resonator can only assume energy values that are multiples of hν, the obvious assumption is that the emission and absorption of light occurs only in these energy quantities. On the basis of this hypothesis, the light-quanta hypothesis, the questions raised above about the emission and absorption of light can be answered. As far as we know, the quantitative consequences of this light-quanta hypothesis are confirmed. This provokes the following question. Is it not thinkable that Planck's radiation formula is correct, but that another derivation could be found that does not rest on such a seemingly monstrous assumption as Planck's theory? Is it not possible to replace the light-quanta hypothesis with another assumption, with which one could do justice to known phenomena? If it is necessary to modify the theory's elements, couldn't one keep the propagation laws intact, and only change the conceptions of the elementary processes of emission and absorption?
To arrive at a certain answer to this question, let us proceed in the opposite direction of Planck in his radiation theory. Let us view Planck's radiation formula as correct, and ask ourselves whether something concerning the composition of radiation can be derived from it.
("On the Development of Our Views Concerning the Nature and Constitution of Radiation", Physikalische Zeitschrift, 10, 817-825, 1909)
Eight years later, in his paper on the A and B coefficients (transition probabilities) for the emission and absorption of radiation, Einstein carried through his attempt to understand the Planck law. He confirmed that light behaves sometimes like waves, at other times like the particles of a gas.
For Teachers
To hide this material, click on the Normal link.
For Scholars
To hide this material, click on the Teacher or Normal link.


 Chapter 1.1 - Creation
Chapter 1.1 - Creation 
 Home
Home 